Les lignes principales des triangles
On survole dans ce premier film d’à peine 5 minutes le troisième cas d’isométrie des triangles, un récapitulatif mnémotechnique des trois cas et enfin la présentation des lignes principales des triangles.
Triangles isocèles
La première vidéo dure 10 minutes et présente la Définition 3.1 de la page 21, ainsi que les points (1), (2) et (3) de la Proposition 3.2, qui fournissent deux critères permettant de reconnaître un triangle isocèle. Prenez des notes de la démonstration sur la page 22 dans votre fascicule! Les autres critères de la Proposition 3.2 (4), (5) et (6) sont discutés ensuite à la page 23, j’en parlerai dans le film suivant.
Caractérisation des triangles isocèles
Dans ce film de 8 minutes nous complétons la preuve de la Proposition 3.2 sur les triangles isocèles.
Triangles équilatéraux
Dans le troisième et dernier film (7 minutes) de cette petite période de cours nous parlons des triangles équilatéraux et identifions le groupe des isométries d’un triangle équilatéral.
Triangles rectangles
Nous terminons le Chapitre 2 sur les triangles. Les deux dernières pages concernent les triangles rectangles. Ce film de 8 minutes rappelle la définition et montre les cas d’isométrie pour ces triangles particuliers.
Les quadrilatères
Le Chapitre 3 concerne les quadrilatères. Nous commençons avec un petit film de moins de 5 minutes qui rappelle les notations, ainsi que les notions de simplicité et de connexité. Vous ajouterez les légendes sous les quadrilatères de la page 27.
Les trapèzes
Un film d’à peine 4 minutes sur les pages 28-29. Ajoutez les hauteurs sur les dessins à la page 28 et recopiez l’argument sur les trapèzes isocèles au haut de la page 29.
Les parallélogrammes
Nous parlons du centre de symétrie d’un parallélogramme (Proposition 3.3). La première minute parle de l’illustration que vous devez faire dans vos fascicules à la page 29, la suite, minutes 1′-6’30, présente la démonstration de la première partie de la proposition, vous pouvez éventuellement faire le dessin en regard du bas de la page 29 pour mieux suivre les explications. Enfin la fin du film, minutes 6’30 -10’30, est à écrire dans l’espace prévu sur la page 30.
Serie29 du 29 avril
Je laisse aussi les indications des autres années, même celles des exercices que nous avons faits ensemble, bravo pour votre travail mercredi “en classe”!
Exercice 8. Partie 2. On suppose que les triangles ABC et A’B’C’ sont isocèles en A (respectivement A’). Les angles en A et A‘ sont isométriques et les hauteurs [AM] et [A’M’] sont isométriques. Les points M et M‘ sont les pieds des hauteurs issues de A et de A‘ respectivement. Pour montrer que les triangles sont isométriques je vous propose de regarder les triangles rectangles BAM et B’A’M’. Y a-t-il un cas d’isométrie des triangles que nous pouvons appliquer pour conclure que ces triangles-là sont isométriques?
Exercice 10. Pour écrire les marches-à-suivre il n’est pas nécessaire de détailler la construction d’une bissectrice, d’une médiatrice, de la perpendiculaire à une droite donnée passant par un point. Ces constructions ont été vues cet hiver et il suffira par exemple de commencer la première marche-à-suivre en disant que l’on construit la bissectrice de l’angle donné.
Exercice 11. On étudie dans cet exercice un triangle ayant deux hauteurs isométriques, comme sur l’illustration suivante où les hauteurs [BH] et [CK] ont même longueur. Nous devons en déduire que le triangle ABC est isocèle, ici en A, c’est-à-dire que les côtés [AB] et [AC] sont isométriques.
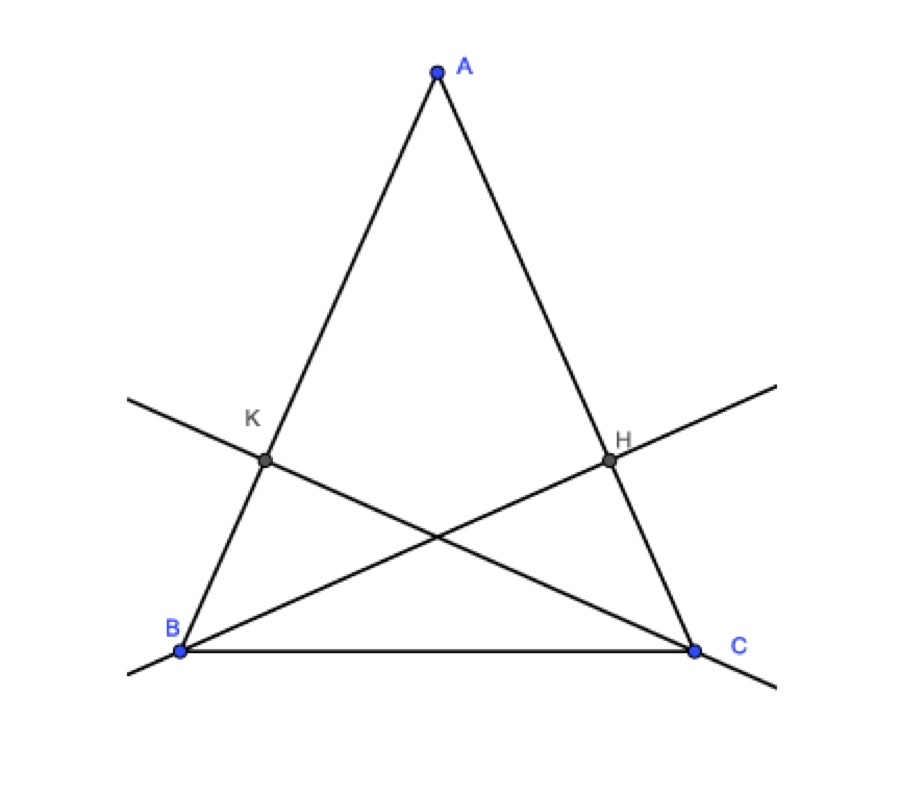
Je vous propose de trouver parmi les triangles de cette illustration deux triangles, l’un ayant [AB] pour côté, l’autre [AC], et qui sont isométriques par un cas d’isométrie des triangles. Il faudra bien sûr utiliser les hypothèses!