The Locomorph project is funded by the FET Proactive ‘Embodied Intelligence’ Initiative within the Information and Communication Technologies (ICT) Work Programme, under the Seventh Framework Program (FP7) of the European Union. The project duration is four years, starting from February 2009. The consortium consists of six universities in five countries.
Project Description
Locomorph’s main objective is to apply the concept of morphology and morphosis to achieve efficient and robust robotic locomotion and movements, in particular, with increased self-stabilization, energy efficiency, maneuverability, and adaptivity to unknown environment. Locomorph combines multidisciplinary approaches from biology, biomechanics, neuroscience, robotics, and embodied intelligence to investigate locomotion and movements in animals and robots, focusing on two concepts: morphology and morphosis.
Morphosis: to extend the concept of exploiting morphology further by investigating morphing, i.e. changing morphology. Voluntary morphosis – the ability to self-adjust own morphology – as a valuable skill for robots, enabling the robots to increase their adaptivity to current tasks and environments. Involuntary morphing is also a relevant issue, since it can occur in robots because of injuries or other external causes.

BioRob Main Contributions
The Biorobotics Laboratory mainly contributes in these subjects of the project:
The objectives of this parts are to implement adaptive sensory-motor control and learning strategies which take advantage of the robots’ natural physical dynamics, to develop strategies for dealing with voluntary and involuntary morphosis and to develop theoretical understanding on how morphology can ease control and learning. The main contribution of BioRob to this part of the project includes:
2.2) Control and learning strategies for different morphologies.
Current Activities
1) Locomorph control and learning framework
The architecture has four main components (Fig.1):
- Lower level motor primitives,
- Morphosis controller,
- Optimizer,
- Supervisor
The role of the morphosis controller is to decide and control when and how to change morphological properties, and that the role of the supervisor will be to monitor performance, to switch between motor primitives for different gaits, to determine when to run the optimization algorithms, and to provide a high-level interface for the human operator.

Fig.1: General architecture of sensory motor control and learning framework
Our first goal: to describe the motor primitives and to give some examples of how they can adapt to a given morphology using optimization tools both offline and online.
2) Central pattern generator control
The underlying neural controller used in most of our studies is the central pattern generator (CPG) (Pouya et al. 2010). Here we are giving a short reminder since the CPG concept is a central component of our control and learning framework.
Central pattern generators are a specific type of neural networks found in the spinal cords of vertebrates (Grillner and Wallen 1985). They produce rhythmic patterned signals used to generate periodic movements like locomotion gaits. A CPG network can intrinsically produce oscillatory outputs without having any periodic input signal, meaning it does not need sensory feedbacks or periodic commands from the higher-parts of the brain to generate coordinated rhythmic activity. However, feedback and descending commands are of course essential for shaping and modulating that rhythmic activity.
In robotics CPGs have been modeled by coupled oscillators that are used to produce rhythmic gaits in robots (Ijspeert 2001, Righetti and Ijspeert 2006, Righetti and Ijspeert 2008, Ijspeert 2008). CPGs are well suited for coevolution studies. Since a CPG is a network of distributed neurons organized as coupled oscillatory sub-networks (oscillators), they can easily be mapped to the morphology of the robot. When some parts of the robot are added or removed, the CPG is adapted by adding or removing the oscillators corresponding to the moving parts. This preserves the other oscillators and thus conserves most of the properties of the initial network. The coordinated rhythmic patterns generated by a CPG produce periodic gaits. Those are the reasons that make CPGs a perfect candidate for the control of our robots.
In our studies an oscillator is typically implemented for each active degree of freedom (DOF). To allow synchronization, these oscillators are then coupled together. The servos controlling the DOFs are governed by the following equations. This controller architecture was designed at BioRob e.g. for the Roombots (Sproewitz et al. 2010, Pouya et al. 2010). Each servo is associated with one oscillator and equations for an oscillator are given below.

Three state variables are defined for each of the oscillator, Фi encodes the phase, ri encodes the amplitude and xi encodes the offset of the oscillator. ψij is the phase bias of the coupling between ith and jth oscillator. Compared with the original controller an additional state for the offset, xi, is added to the dynamical system. The frequency of the system ν is typically used as a fixed parameter that is not optimized but we also performed studies where the frequency is a function of the phase variable. The weight of the couplings (ωij) are fixed as well. a and b are positive constants which only affect the rise time of the state variables. The amplitude Ri, the phase bias ψij and the offset Xi are typically open variables that are subject to optimization.The servo driving functions which are given in Equation (4)-(6) support two types of basic movements, namely oscillation and rotation.
3) Verification of Controller-Optimizer Framework on Roombots
- Combinig proposed controller architecture with optimization algorithm for optimal gait generation
- Designing CPG topology based on robot morpholgies (Fig. 3).

Fig.3: Pictures1 of different modeled robot morphologies by using roombots modular robot to verify the framework including four different metamodules, two quadrupeds and one arbitrary asymmetric shape. Their corresponding CPG network mimics the physical topology by coupling neighbor oscillators.
1) Thanks to Jesse van den Kieboom for the pictures.
Results for Hybrid Learning:
The movie “Hybrid_learning” below shows how hybrid framework for controller-optimizer optimizes the CPG in two levels; first the CPG structure by finding suitable movement type for each active servo and second the open parameters of CPG such as amplitude and offset of the movement. In this simulation, until iteration number 80 optimizer is exploring different combinations of movement types (including oscillation, clock-wise, counter-clock-wise rotation and locked modes) to find the best configuration. After finding the best, from iteration 80 to 100, it optimizes the open parameters of each joint to increase the speed.
4) Application of the framework on Locomorph robots
The goal is to facilitate the robot development by pre-evaluating possible robot designs in simulation with our control and learning framework and to optimize control architectures that then can easily be transfered to the real hardware. See Figure 4 for two different models of the UZH1 design created in Solid Works (left) and the model simulated in Webots (right). This robot has been designed by our partners from University of Zurich. We successfully applied our control and learning framework both to the Locokit and to several iterations of quadruped robot designs.

Figure.4: Example of transfer of robot model from design software to simulation environment. (Left) UZH1 robot design in Solid Works. (Right) UHZ1 robot model forsimulation in Webots.
5) Studies on the spring-loaded inverted pendulum (SLIP) model
One of the main objectives of the Locomorph project is to gain a deeper understanding how control and learning strategies can take advantage of the robots’ natural physical dynamics. To address this objective we decided to study the spring-loaded inverted pendulum (SLIP) in more detail.
The SLIP model is a simple physical model to analyze data of human and animal running. By means of that, different quantities observed experimentally are related to each other and it appears that there is great similarity in running of different species. Furthermore, the SLIP model is used to synthesize stable running patterns in a forward dynamic simulation. The occurrence of passively stable running patterns is remarkable. It appears due to the intermittent ground contact (non-holonomic stability; Ruina 1998). From the SLIP we could thus learn how to build robots that can perform passively stable running and how to make use of the robots’ compliance for more robust, stable and energy-efficient locomotion.
6) Coevolution of Morphology and Control
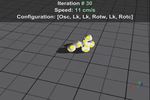
Not every robot morphology is optimal for control or can even be controlled. Our coevolution studies have been performed to address one of the main objectives of the Locomorph project – the question for the theoretical understanding on how morphology can ease control and learning. To address this question we carried out several studies. For the optimization of morphology and control we are using Evolutionary Algorithms (EA). EAs are methods inspired by the evolution of the genome in living organisms where new organisms with varying properties can be created in every generation since they inherit a mix of the DNA of their parents that can be further modified by so-called mutations. Both studies were carried out in simulation using the Webots simulator(Michel 2004).
In the studies we were using our central pattern generator approach. For each active degree of freedom we implemented a phase oscillator. The coupling of these individual oscillators was subject to optimization by the EA.
The first study (Aydin 2010) addressed the question of how we can optimize robot morphology and control to gain robots capable of fast, energy efficient and safe locomotion comparing compliant and non-compliant modular robots. This study was carried out using our Roombots modular robot setup (Sproewitz et al. 2010). Figure 2 is showing a single Roombots module with three compliant legs. To code the genome of the robots we studied the so-called L-systems that initially have been developed to model the growth process of the organisms (Floreano and Mattiussi, 2008). We were able to evolve robots performing efficient locomotion and could prove that the addition of compliant structures are beneficial for the robot locomotion.

Figure.2: A Roombots module with three passive legs. Passive legs are rendered with a red connection face and a sphere. Picture taken from (Aydin 2010).
The second study (Larpin 2011) made largely use of the tools that had been developed in the first work. However to better address the ideas of the Locomorph project we decided to shift the focus of our attention more towards legged robots. See Figure 3 for several example robot configurations. Furthermore we generalized the underlying selection methods for finding the optimal robot morphologies and control networks. As in previous studies the fitness criteria included the speed and the energy efficiency of robot locomotion but while previous studies typically concentrated on finding morphologies and control parameters for allowing the robot to move as fast as possible on a straight line we concentrated in this project as well on the steering capacity of the robot. To make a robot useful, manoeuvrability is indeed as important as energy efficiency and maximal speed.

Figure.3: Example robots from coevolution study. Picture taken from (Larpin 2011).