ORB5

ORB5 is a global, gyrokinetic, Lagrangian, Particle-In-Cell (PIC), finite element, electromagnetic, GPU-enabled code developed at SPC, with important contributions from the Max-Planck IPP in Garching and Greifswald and the University of Warwick. The ORB5 code features [1-8]

  • a global approach for both plasma and background magnetic geometry, which can be obtained from axisymmetric ideal MHD equilibria computed with the CHEASE code [9]
  • multi-species plasma
  • kinetic electrons, or various approximate models: hybrid-trapped or adiabatic
  • intra- and inter-species linearized collision operators
  • electromagnetic perturbations, with the cancellation problem solved using enhanced control variates and a ‘pullback’ scheme
  • various noise reduction and noise control techniques: flow-conserving Krook operator, coarse graining, quadtree-based weight smoothing
  • 3D finite elements with B-spline basis functions up to 3rdorder
  • field-aligned Fourier filter eliminating unphysical modes
  • full-f features (although the polarization density is linearized)

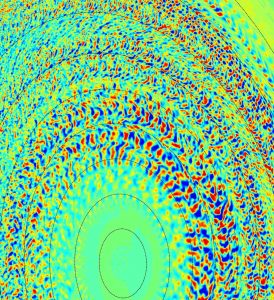On the numerical side, the ORB5 code has been completely refactored in 2016-2018, with a new data structure and its parallelism enhanced, partly under a PASC Co-design project. Originally a pure MPI code based on domain decomposition and domain cloning, it now features:

  • hybrid MPI/OpenMP and MPI/OpenACC parallel programming models
  • various multithreading algorithmic options for the various kernels, in particular for the gyro-averaged charge and current deposition and field assignment
  • single master source code encompassing all functionalities mentioned above, and which can be run either on CPU-only or on GPU-equipped HPC systems.

The GPU is really accelerating the code. For an electromagnetic simulation, the code runs 4 times faster when using the GPU than when using the 12-core CPUs on the Piz Daint Cray XC50 at CSCS. For a large dataset, running ORB5 on 512 nodes with GPU is 1.5 times faster than running on 2048 nodes without using the GPU, the amount of resources (node-hours) to get to the solution is reduced by a factor of 6, and the energy-to-solution reduced by a factor 8.5.

[1] T.M. Tran, et al., Theory of Fusion Plasmas, International School of Plasma Physics – Piero Caldirola, Joint Varenna-Lausanne Int. Workshop, Varenna, Aug.31 – Sep 04, 1998, Vol.18, p.45
[2] S. Jolliet, et al., Comput. Phys. Commun.177,409 (2007) https://doi.org/10.1016/j.cpc.2007.04.006
[3] B.F. McMillan, et al., Phys. Plasmas15, 052308 (2008) https://doi.org/10.1063/1.2921792
[4] A. Bottino, et al., IEEE Trans. Plasma Sci.38, 2129 (2010) https://doi.org/10.1109/TPS.2010.2055583
[5] T. Vernay, et al., Phys. Plasmas17, 122301 (2010) https://doi.org/10.1063/1.3519513
[6] J. Dominski, et al., Phys.Plasmas24, 022308 (2017) http://dx.doi.org/10.1063/1.4976120
[7] N. Tronko, et al., Phys. Plasmas24, 056115 (2017) https://doi.org/10.1063/1.4982689
[8] A. Mishchenko, et al., Phys.Plasmas24, 081206 (2017) https://doi.org/10.1063/1.4997540
[9] H. Lütjens, A. Bondeson, O. Sauter, Comput. Phys. Commun.97, 219 (1996) https://doi.org/10.1016/0010-4655(96)00046-X