MIT Press Book: “Learning for Adaptive and Reactive Robot Control”
The book can be purchased from MIT Press here.
NEW WEBSITE AVAILABLE HERE
Content
This book presents a wealth of machine learning techniques to make the control of robots more flexible and safe when interacting with humans. It introduces a set of control laws that enable reactivity using dynamical systems, a widely used method for solving motion-planning problems in robotics. These control approaches can re-plan in milliseconds to adapt to new environmental constraints and offer safe and compliant control of forces in contact. The techniques offer theoretical advantages, including convergence to a goal, non-penetration of obstacles, and passivity. The coverage of learning begins with low-level control parameters and progresses to higher-level competencies composed of combinations of skills.
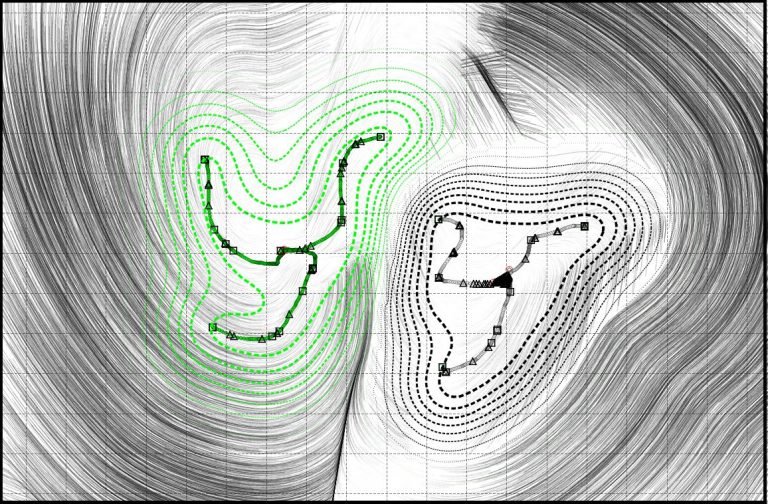



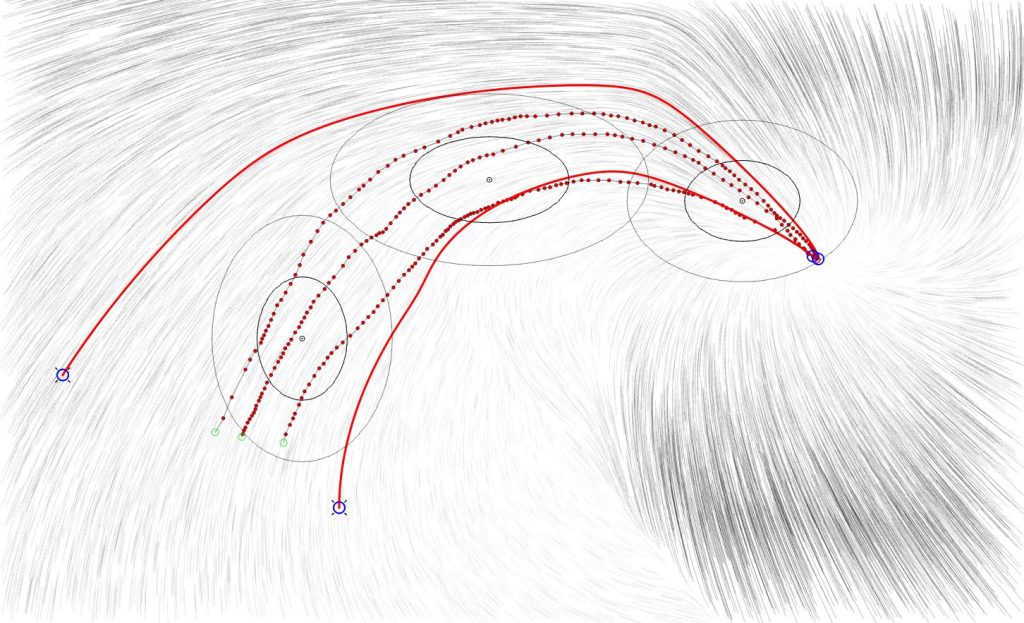
Structure
The book is meant to be used as Textbook for graduate-level courses in robotics, and, hence, the chapters proceed from fundamentals to more advanced content. The first section presents an overview of the techniques introduced, including learning from demonstration, optimization, and reinforcement learning. Subsequent sections present the core techniques for learning control laws with dynamical systems, trajectory planning with dynamical systems, and methods for compliant and force control using dynamical systems.
Each chapter describes applications, which range from arm manipulators to whole-body control of humanoid robots, and offers both pencil-and-paper and programming exercises.
Lecture videos, slides, handwritten and programming exercises instructions and MATLAB code for the exercises are available in the table below.
Material for Lecturers
The course presented here, whilst based on the book, had to be adapted to the 13 weeks semester format. Some chapters are therefore only briefly covered in the last lecture.
Moreover, practical sessions are proposed, where students can experiment with the complete pipeline of learning a control law with dynamical systems. The first two sessions are Matlab simulations and in the last one a Franka Emika Panda robot is used to teach and learn a dynamical system.
The complete schedule is shown below. It contains all the available content for the course, along with references to book sections.
| Week | Topic | Book Chapter | Slides | Lecture videos | Exercises Instructions | Code for MATLAB exercises |
|---|---|---|---|---|---|---|
| 1 | Introduction to robot path planning | Ch. 1 | Intro | x | x | x |
| 2 | Acquiring data for learning | Ch. 2 | LfD | x | x | x |
| 3 | Introduction to Dynamical Systems (DS) | App. A | DS | x | x | x |
| 4 | Learning Control laws with DS | Ch. 3 | ML SEDS LPVDS | x x | x | x |
| 5 | Matlab Practice Session I | x | x | |||
| 6 | Learning how to Modulate a Dynamical Systems | Ch. 8 | Modulation | x | x | x |
| 7 | Obstacle avoidance with Dynamical Systems | Ch. 9 | Obstacle | x | x | x |
| 8 | Matlab Practice session II | x | x | |||
| 9 | Impedance control with Dynamical Systems | Ch. 10 | Impedance | x | x | x |
| 10 | Force control with Dynamical Systems | Ch. 11 | PassiveDS | x | x | x |
| 11 | Extensions & other applications to learning with DS | Ch. 4, 5, 6 & 7 | Extensions | x x | ||
| 12 | Overview and exam preparation | Overview | ||||
| 13 | Franka Robot Practice Session III | x |
Solutions
Solutions to both pen and paper and programming exercises offered in the book can be obtained by lecturers upon request. These are given only to lecturers who have purchased the book and if these solutions are to be used in a course. You can request the solutions here by clicking on ‘Digital Exam/Desk Copy’ and choosing supplemental materials afterwards.
Software
The complete Matlab code in support of programming exercises is available on the book’s Github page. Solutions to Practicals I and II are publicly available on a separate branch. All others solutions must be requested through the MIT Press portal.
Lecture Videos
Complete videos of Professor Billard’s lectures from 2022 and 2023 can be found on EPFL’s mediaspace.
Overview
An overview of each chapter is presented below, along with videos of the robotic implementations. Videos of the corresponding lecture are shown at the start of each description, along with links to the slides and to the exercises instructions.
All videos of the experiments displayed below are available on LASA’s youtube page.
All public content for the course is available in the table above.
Lecture 1 – Introduction
Slides | Exercises
This chapter introduces the core concepts detailed in the rest of the book, starting with the fundamental robotics problem of planning a trajectory in free space. Globally convergent, accurate and fast motion planning is a challenge to execute which depends largely on robot design and knowledge of the environment. To face this challenge, path planning using dynamical systems offers a robust, stable and reactive solution, provided the dynamical system is adapted to the required task.
This book proposes several machine learning methods to learn a dynamical system through demonstrations, as well as techniques to generate a viable dataset of trajectories. Using these methods, one can learn a variety of control laws specifically suited for tasks such as precise manipulation or navigation.
In the following chapters of the book, methods to augment these controllers through coupling and modulations are presented. These techniques allow robots to interact with external objects and even other robots. Modulations can even be used to implement obstacle avoidance using dynamical systems, as is shown in Chapter 9.
The last section demonstrates how compliant and force control can be derived using dynamical systems. These types of controllers are essential for safe human-robot interaction in the workplace due to their compliance in contact phases and robust force control in the face of disturbances.
Lecture 2 – Learning From Demonstration
Slides | Exercises
This chapter presents techniques to gather data which can then be used to train a robot’s controller, as well as the caveats of these methods.
Two popular approaches are Learning from Demonstrations, where an expert provides examples for the desired task, and Reinforcement Learning, where the robot learns through trial and error by exploring the task space. Optimal Control can also be used to generate large sets of feasible trajectories. Each method has different requirements and the choice of which method to use depends on factors such as the desired task, the prior knowledge of the robot and environment, the trainer and the time available.
Several interfaces for teaching robots via human demonstration are presented here, namely teleoperation, kinesthetic teaching and observational learning. These demonstrations require no model and can be done by anyone, however the quality of the learned controller greatly depends on the quality of the dataset. Therefore, the respective challenges of each interface, as well as general considerations for constructing optimal datasets are also proposed.
Finally, as is done for each chapter, a robotic implementation is shown, demonstrating how each method can be used to train a robot to play golf.
Lecture 3 – Introduction to Dynamical Systems
Slides | Exercises
Lecture 4 – Part 1: Why Machine Learning is Not Sufficient
Slides | Exercises
Lecture 4 – Part 2: SEDS and LPV-DS
SEDS & LPV-DS | Exercises
This chapter details methods to learn a control law for robot motion generation using time-invariant dynamical systems (DSs). Our training data consists of sample trajectories, which cover a limited portion of the state space. The goal of the learning algorithm is to reproduce the training data well, while generalizing over the rest of the workspace. In particular, we must ensure that the system does not diverge from the training data. In short, we wish to learn a function which reproduces the provided reference dynamics and converges to a single stable equilibrium point, also called the target or attractor. From a machine learning perspective, estimating ẋ = f (x) from data can be seen as a regression problem, where the inputs are the state variables x and the outputs are their first-order derivatives ẋ.
The first section of this chapter therefore introduces three classic regression methods to estimate f and demonstrates their inability to learn a stable DS. Indeed, the DS learned using these methods is not guaranteed to be globally convergent to the attractor and is therefore insufficient as a control law. Hence, we briefly introduce Lyapunov theory for stable DSs, from which we derive conditions for the stability of linear DSs.
Robots are however often required to perform nonlinear motions which cannot be represented with a single linear DS. Moreover, stability analysis of nonlinear DS is still an open question and theoretical solutions exist only for particular cases. In this chapter, we offer a solution to this problem by formulating nonlinear DS as a mixture of linear systems, a formulation which is very similar to the Gaussian Mixture Regressor (GMR) equation. In order to learn our nonlinear DS, we exploit this ressemblance by formulating a constrained GMR learning algorithm referred to as the Stable Estimator of Dynamical Systems (SEDS). This algorithm is presented, evaluated and implemented on a robot in this section.
While the SEDS algorithm guarantees global convergence, it suffers from a few limitations: lack of incremental learning, no modeling of highly nonlinear motions and sensitivity to hyperparameters. The next section of this chapter proposes a new approach that tackles these limitations : the Linear Parameter Varying Dynamical Systems (LPV-DS). Using a physically consistent estimation approach for Gaussian mixture models as the initialization of hyperparameters, it is then possible to learn highly non linear motions. We further propose methods for offline and incremental LPV-DS parameter optimization, before presenting an evaluation of this algorithm. This section concludes with three implementations of the LPV-DS method to learn control laws for robotics systems.
Until now, only first order DS were considered. In the last section of this chapter, we extend the previously presented approaches to learn second-order DSs. Again, this section ends with an evaluation of the presented algorithm and a robotic implementation.
Lecture 12 – Extension to Control with Dynamical Systems
Slides
This chapter presents how to learn multiple control laws with distinct dynamics and attractors. We show how to embed these laws in a single continuous function, which facilitates switching across laws at run time but increases the learning complexity. In the two sections of this chapter, we present two approaches to this problem, one using state-space partitioning, the other through bifurcations.
The first approach is is called the Augmented SVM framework and which partitions the state space so that each partition has one DS with its own attractor. This method inherits the region partitioning ability of the well-known Support Vector Machine (SVM) classifier augmented with novel constraints for learning the demonstrated dynamics and ensuring local stability at each attractor.
In the second section of the chapter, we show how we can learn a DS valid through the entire state, whose characteristics can be modified through an external parameter. This is akin to the principle of bifurcation in DS theory. We show that we can embed fixed point attractor DS and limit cycles in a single DS. Furthermore, we show that we can learn complex limit cycles through diffeomorphism.
Lecture 12 – Extension to Control with Dynamical Systems
Slides
When a robot is perturbed during task execution, it might fail to achieve some of the high-level requirements/objectives of the task at hand, such as: (i) Following precisely (or tracking) the reference trajectories used to learn the DS; and (ii) Reaching via-points or subgoals that might be crucial to accomplish a task.
In this chapter we offer approaches that endow the controller with the capabilities of accomplishing task objectives (i) and (ii), while preserving state dependency and convergence guarantees. We posit that (i) and (ii) can be achieved via the DS motion generation paradigm by modeling the robots’ task as a sequence of DS.
Tracking a reference trajectory: In this first section, we introduce a DS formulation that is capable of trajectory-tracking behavior around a reference demonstration, while preserving global asymptotic stability (GAS) at a final attractor. This DS formulation, referred to as locally active globally stable DS (LAGS-DS), models a complex nonlinear motion as a sequence of local virtual attractor dynamics. These local dynamics encode different trajectory tracking behaviors in linear regions around the nonlinear reference trajectory. Further, they are virtual, as the DS does not stop at the local attractors but rather smoothly transits through them if the robot is within the locally active regions.
Reaching via-points: To achieve this, the task could be modeled as a sequence of single-attractor nonlinear DSs, here each non-
linear DS’s attractor is located at the intermediary target. In this second section, we introduce a formulation based on hidden Markov models (HMMs) that sequences nonlinear DS in a probabilistic manner. We refer to this approach as the HMM-LPV, as it uses the LPV expression for DS introduced in chapter 3. We show that we can ensure that the stability guarantees of each individual DS at its respective attractor are preserved throughout the sequencing of the task. The overall dynamics is, hence, guaranteed to transition through each via-point.
Lecture 12 – Extension to Control with Dynamical Systems
Slides
In previous chapters, we always assumed that we were controlling a single agent. However, it is often useful to control several agents simultaneously. The agent may be several robots or simply several limbs of one robot. Simultaneous control allows the systems to act in synch. It also allows one to generate precedences across the movement of the various systems.
To generate such dependency across different systems, we use mathematical coupling across the dynamical systems (DSs) at the basis of the controllers of each agent. The notion of coupling is core to DS theory and appears when there is an explicit dependency across two or more dynamics. This chapter presents examples in which explicit couplings across dynamical systems-based control laws can simplify robot control while preserving the natural robustness against perturbation.
The first section introduces the type of dependencies considered in this book. The next section shows how coupling across DSs can be used to enforce that the DS follows a precise trajectory in space. The third section presents another application of coupling across DSs for robot control. Coupling is used to control the arm and hand of a robot. One DS controls the arm movement in space, while a second DS controls the fingers of the robot’s hand. The hand is coupled to the arm, as its DS depends on the state of the arm. This allows one to synchronize the arm and hand movements to ensure that the hand closes on the object once the arm reaches the object. This coupled arm-hand DS offers a natural robustness to disturbances.
In the last section of the chapter, this principle is extended to couple the eyes, arm, and hand of the robot through a hierarchical coupling across three DSs. The DS of the eyes drives the movement of the arm, while the DS of the arm drives the DS of the hand. This system enables the smooth visual pursuit and grasping of a moving object. It can also be used to track a isually moving obstacle and steer the arm and hand away from the obstacle.
Lecture 12 – Extension to Control with Dynamical Systems
Slides
In chapter 6, we saw how dynamical systems (DSs) can be coupled to enable joint control of multiple limbs in a robot. In this chapter, we show how we can take this coupling one step further and couple the DS controlling our robot to the dynamics of an external object over which we have no control. To emphasize the need for immediate and fast replanning, we consider scenarios in which the dynamics of the object can change abruptly and the object moves very quickly.
Specifically, we tackle the problem of intercepting a moving object. We assume that all we have at our disposal is a model of the object’s dynamics, but that this model may change over time. To move in synch with the object’s dynamics, we couple the robot’s motion to that of a virtual object. The virtual object’s dynamics takes the role of an external variable to which we can couple the robot’s DS. We show that a strategy that enforces a coupling with the object’s dynamics, and whereby the robot adapts to the object’s velocity, improves the stability at contact by decreasing the impact force.
The first section of this chapter formalizes the problem and the envisioned applications. The next section starts the technical part of this chapter by reformulating control of trajectories with a second-order DS. In the third section, we present an approach in which the robot’s motion can be coupled to that of a moving object. We show an application for catching fast-moving objects in flight. We formulate stability constraints to ensure that the robot meets the object and, once it does so, that its velocity is aligned with the object’s velocity. This allows the robot and the objects to move in synch and hence mitigates impact forces and prevent the object from bouncing off the robot’s hand. The last section extends this approach in order to enable a moving object to be intercepted synchronously by two robotic arms.
Lecture 6 – Learning to Modulate a Dynamical System
Slides | Exercises
In the previous chapters, we have shown various techniques to learn a control law from a set of training data points. This learning was done once for all, offline, based on examples from a full set of training trajectories. There are, however, many occasions when it would be useful to be able to train the system again, such as to enable a robot to take a different approach path toward a target. Often, the changes apply only to a small region of the state space. Hence, it would be useful to be able to retrain the controller by modifying the original flow only locally.
This chapter shows how one can learn to modulate an initial (nominal) dynamical system (DS) to generate new dynamics. We consider modulations that act locally to preserve the generic properties of the nominal DS (e.g., asymptotic or global stability). We further show how such modulations can be made explicitly dependent on an external input and illustrate the usefulness of such a concept with a few examples where the speed is modulated to enter in contact with a surface.
We start the chapter with a description of the properties required for the modulation. We then introduce several methods to learn and construct the modulated functions for internal and external signals in the second and third sections, respectively. Finally, we consider a scenario where a robotic system should stably contacts a surface.
Lecture 7 – Obstacle Avoidance with Dynamical Systems
Slides | Exercises
In the previous chapters, we always have assumed that the control law was valid throughout the entire state space. This is not the case, however, when there are obstacles along the path or when the workspace is limited, as is common when controlling the movement of a robotic arm. While the workspace of a mobile robot may be limited due to the presence of external obstacles, the workspace of the robotic arm is constrained by joints’ limits, which create dead-locks.
In this chapter, we show that, in order to address this problem, one can locally modulate the dynamical system (DS) to contour obstacles or to remain within a given workspace. Importantly, while doing so, we can preserve some of the inherent properties of the DS, such as convergence on a given target.
We start with a modulation that allows for avoiding convex obstacles, and then extend it to concave obstacles and to multiple obstacles in movement. We show that the formulation can also be used to enforce a flow to move inside a volume, which would be useful to ensure that the path stays within the robot’s workspace.
As the method assumes that the shape of the obstacle is known, we discuss how, in practice, one can estimate the obstacles’ shape at run time from a point-cloud rendered by proximity sensors, and how the obstacle’s shape can be learned through scanning of the object.
Obstacle avoidance is particularly useful for controling robots in joint space to avoid self-collision. The boundary of free space in joint space is not fixed, however; it evolves with joint motion. It is also very nonlinear. This is a problem ideally suited for machine learning. In the last section, we show how such a moving boundary can be learned by knowing the kinematics of the robotic systems. The learned boundary can then be used at run time in conjunction with DSs to prevent two robot arms from intersecting with each other, while they rapidly modify their trajectories to track moving targets.
Lecture 9 – Impedance Control with Dynamical Systems
Slides | Exercises
The previous chapters of this book have been devoted to using dynamical systems (DSs) to generate trajectories for position or velocity control of robots. However, we did not control for forces. Force control is necessary for many tasks, such as the precise and fine manipulation of objects, and for mitigating risks if the robot enters in contact with humans.
In this chapter, we show how DSs can be combined with impedance control, an approach traditionally used to perform robust torque control, to perform torque control. Impedance control can be shaped in such a way as to enable robots to absorb interaction forces and dissipate energy at contact. This is particularly useful when contacts may be undesired as the result of unexpected disturbances, such as bumping into an object inadvetently, and to make robots safer in the presence of humans. It is, however, often difficult to determine beforehand what the right impedance would be for a given task. For this reason, many methods have been offered to learn what is the right impedance to apply, when, and where. This chapter reviews some of these and shows how learning of variable impedance can be done in conjunction with learning a DS based control law.
This chapter is organized as follows. The first section discusses the need to provide compliance when in contact with the environment. This is followed by an introduction to compliant control architectures for controlling robots once they are already in contact with an object, presented in the second section. In the next section, we offer two approaches to learn compliant behaviors. Finally, in the last section, we show how this framework can be combined with DSs.
This chapter is organized as follows. The first section discusses the need to provide compliance when in contact with the environment. This is followed by an introduction to compliant control architectures for controlling robots once they are already in contact with an object, presented in the second section. In the next section, we offer two approaches to learn compliant behaviors. Finally, in the last section, we show how this framework can be combined with DSs.
Lecture 10 – Force Control with Dynamical Systems
Slides | Exercises
Force control is essential to robotics. This is required in all tasks that require manipulating objects dexterously. Typical interactive examples include polishing, assembly, cooperative manipulation, and telemanipulation. Force control is required to stabilize robots and for safety in human-robot interaction. In this chapter, we combine force control with the impedance-based DS introduced in chapter 10 to provide robust control of forces in unforeseen situations and in the face of disturbances.
In chapter 10, we introduced DS-based algorithms for providing compliant behavior in contact phases. This chapter presents control architectures that enhance the interactions by controlling the interaction forces while being compliant. We show how we can simultaneously control the force and the motion of a robotic system when moving on non planar surfaces.
We started this book by advocating for robots to be adaptive and to react to disturbances within milliseconds. We took the view that this could be achieved by providing robots with control laws that are inherently adaptive. We chose to use time-invariant dynamical systems (DSs), because they embed multiple paths, all solutions to the problem, and that they do so in closed-form. This enables robots to switch at run time across paths without the need for replanning.
Moreover, we showed that a variety of mathematical properties stemming from DS theory could be used to our advantage to provide guarantees on stability, convergence, and boundedness for control laws. We presented a variety of methods that can be used to learn the control laws from data while preserving these theoretical guarantees. Combining machine learning with DS theory draws on the strength of both worlds and allows us to shape robots’ trajectories, to avoid obstacles, modulate forces at contact, and move in synchrony with other agents, as required for the task at hand.
Research never stops, and much remains to be done. Among the topics that need immediate attention, we believe the following are most important:
- Control in joint space and Cartesian space
- Learning region of stability
- Closed-loop force control
- Inverse dynamics
To close, we thank readers for their interest in this book and we hope that they will find these approaches useful for their work.