Research topics
Dynamical system (DS) based control approaches offer a framework for robust control with the capability of fast adaptation from unexpected perturbations. In this project, we use time-invariant DSs to model complex movements, such as combined control of limb motion, from the collected human demonstration data with single or multiple equilibrium states.
Learning Dynamical Systems with bifurcation
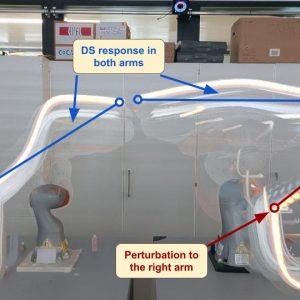
DS for controlling rhythmic patterns are distinct from DS used to control point-to-point motion and current approaches switch at run time across these to enable multiple behaviors. This, however, may lead to jittering and jerky motions when switching across dynamics when these have different equilibrium. The figure below shows a robotic task (polishing) that requires multiple switches from point-to-point motion to cyclic ones.
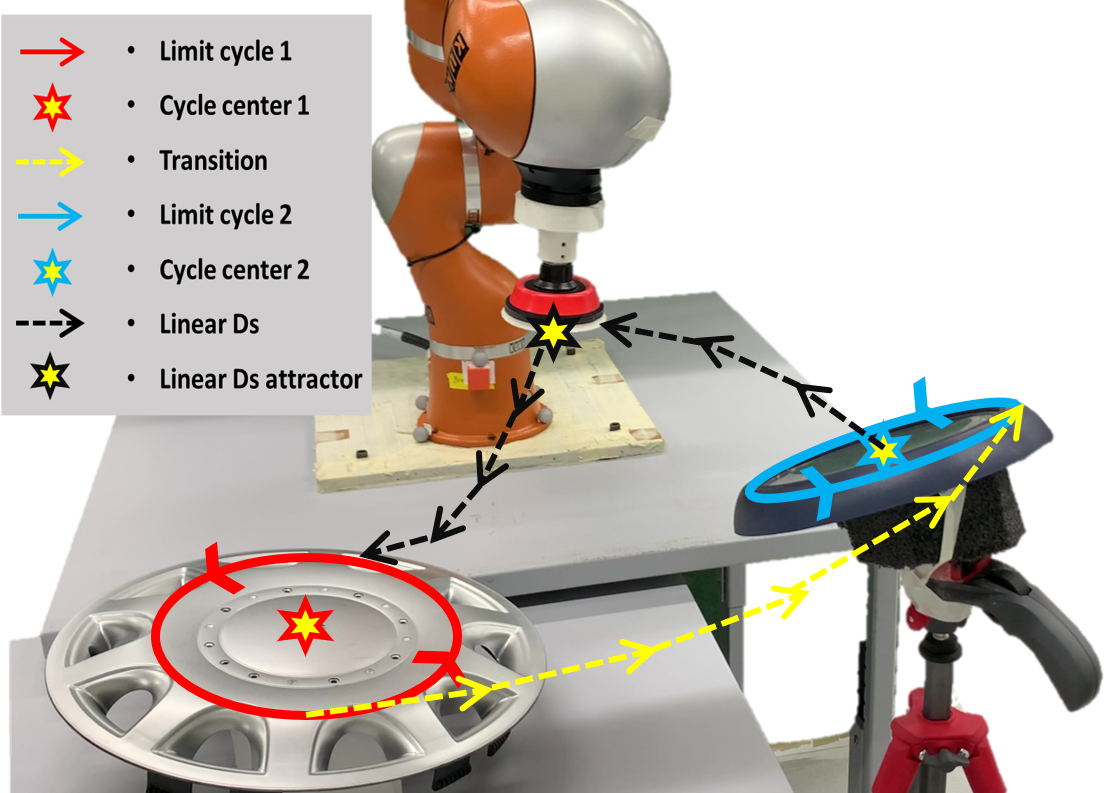
We here offer an approach that encodes periodic and discrete dynamics in a single time-invariant DS by exploiting the concept of bifurcation, allowing for smooth transitions between the two. The following figure manifests the result of the case where bifurcations are exploited in the desired DS.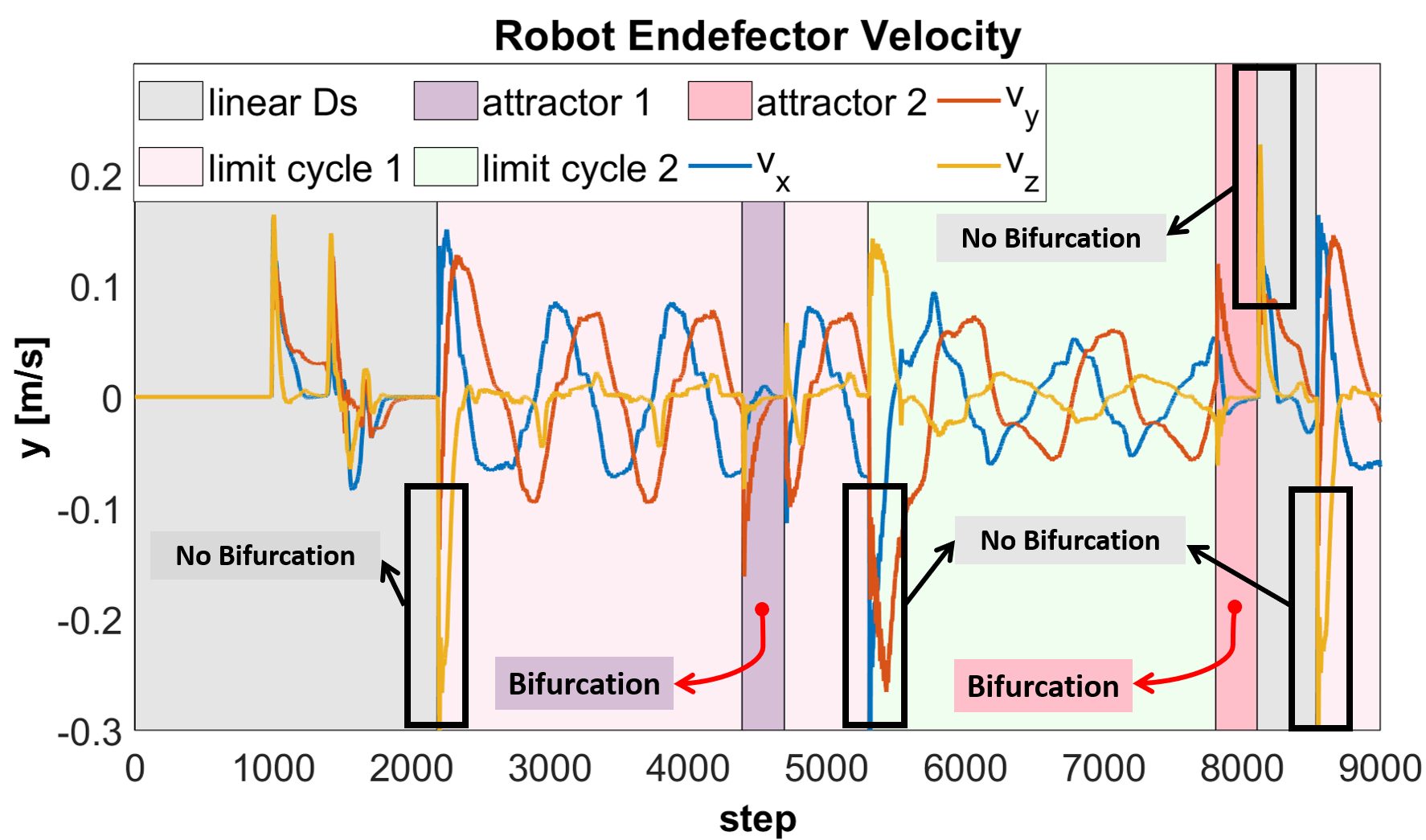
To learn a desired periodic motion, we propose a parameterization of the DS to offer an explicit way to control for its behavior, namely speed, location of the target, and shape of the limit cycle. Furthermore, we also explore the use of diffeomorphism and learn a mapping function to modify the initial linear limit cycle into a nonlinear limit cycle. The video below depicts our approach to learn complex-shaped non-linear limit cycles:
Learned Dynamical System from Human Demonstration Data
Dynamical systems offer a robust control of the robot, by allowing to adapt the movement rapidly in case of perturbations. In fact, as we can see in the figure below, we can generalize collected movement data (shown in red) to the whole workspace (blue arrows). The diagram shows a model that can switch between a point-to-point motion towards an attractor (reaching the screw in a. and going back in c.) and a periodic motion (b.), such as that of screwing or unscrewing that we find in watchmaking tasks.
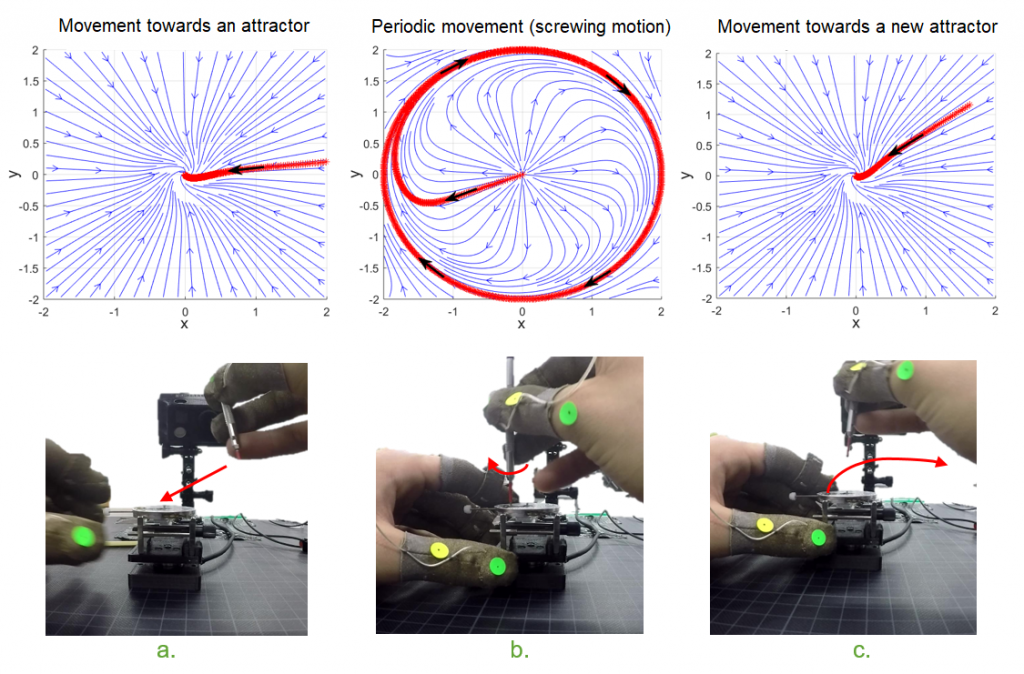
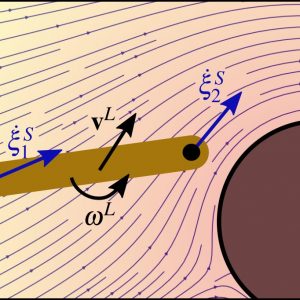
As illustrated in the figure below, a DS model can also be exploited for embedding velocity and force to enable admittance control during a haptic task with an attractor at the origin. This DS modelling may be useful for the control of interactions in bimanual tasks including the interaction of forces.

Learned dynamical systems from human demonstration data
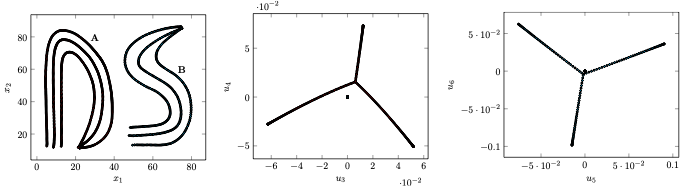
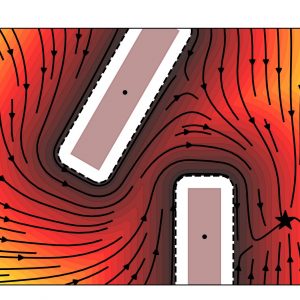
Dynamical systems with multiple equilibrium points are interesting for robot control, as they allow to easily switch across dynamics without incurring discontinuities. While most works assume that the number and type of dynamics are known, we focus on a scenario where unlabeled observations of the dynamical system are given. Determining the number of sub-dynamics and the equilibria’ locations is difficult and can be rarely done analytically. We propose a Graph-based spectral clustering method that takes advantage of a velocity-augmented kernel. We apply the algorithm to identify dynamics of a series of dynamics. We compare our algorithm to Kernel K-Means, Spectral Clustering and Gaussian Mixtures and show that, even when these algorithms are provided with the true number of sub-dynamics, they fail to cluster them correctly.

The proposed method is based on the eigenvalue decomposition of the Laplacian matrix applied to a specific graph structure. Exploiting the spectral properties of the Laplacian matrix, we show that we can cluster and project each sub-dynamics in orthogonal embedding spaces. Moreover, in these embedding spaces, each sub-dynamics is linearized and it is possible to identify the position of the equilibrium point.

Learning latent dynamical system
This research aims to learn latent simplistic and low-dimensional dynamical systems from high-dimensional and nonlinear demonstrations which can be obtained during the watchmaking process. The latent dynamical systems are globally exponentially stable and can be used, not only for learning complex dynamical systems, but also for trajectory clustering and classification. We consider exponential stability guarantees which are be obtained from different stability theories such as Lyapunov and Contraction. Furthermore, we investigate the impact of those on the accuracy of the learned model and their robustness to noise and sparse data.
Modeling of DS in Enclosed Boundary and Stability
Modulation Based Obstacle Avoidance
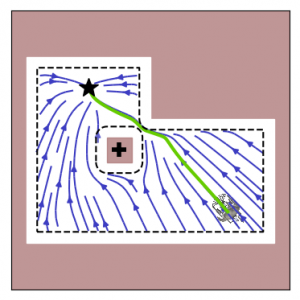
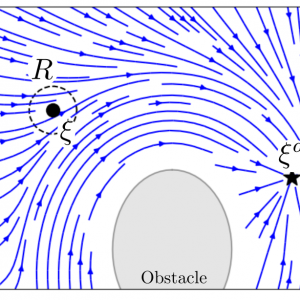
Closed-form dynamical systems (DS) have proven suitable for dynamic applications as no re-planning is required. Describing the obstacle avoidance as a modulation of the initial dynamics ensured that attractors are conserved.
Constraining Motion within Boundaries
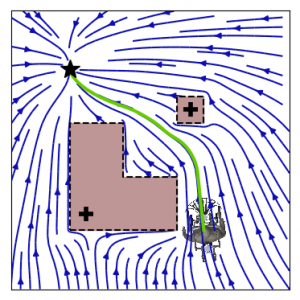
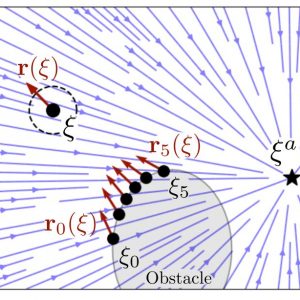
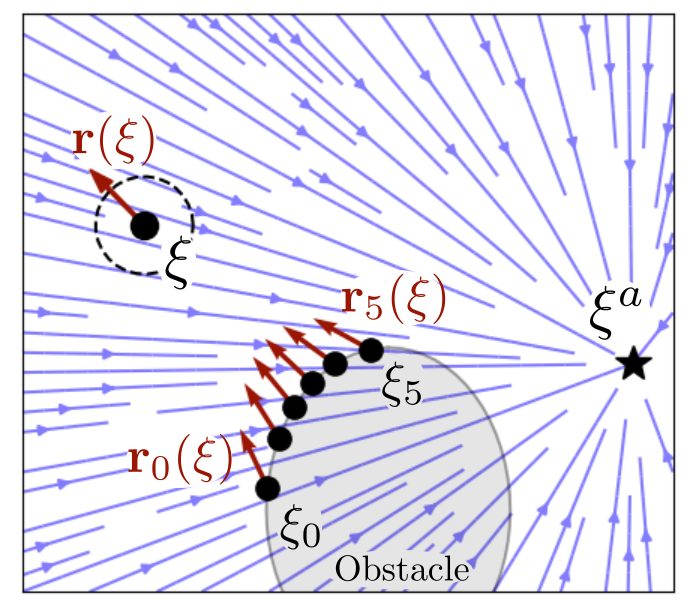
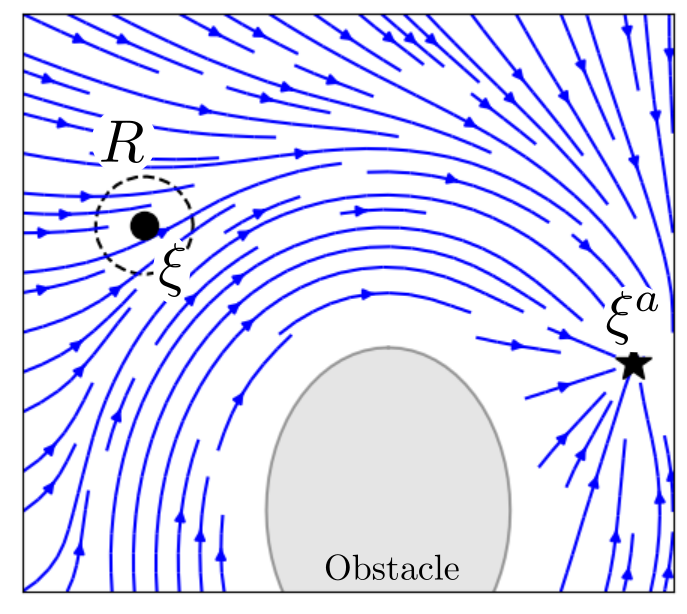
An autonomous robot might be in a scenario where it has boundaries that cannot be passed. This might be a wall for a wheeled robot, or it can be safety or joint limits for a robot arm. This is stated as the constraint of staying within an obstacle. The boundary of the obstacle represents the limits of the free space. If we use the previously introduced obstacle description to denote enclosing hulls, the interior points of the classical obstacle become points of free space of the enclosing hull and vice versa. In many practical scenarios, a hull entails gaps or holes through which the agent enters or exits the space (e.g., door in a room). The inverted obstacle avoidance slows the agent down to zero while trying to approach this exit. For this reason, a guiding reference point for boundary obstacles is introduced.
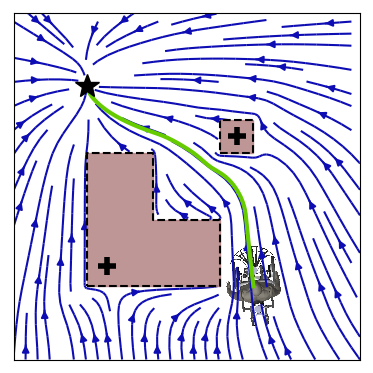

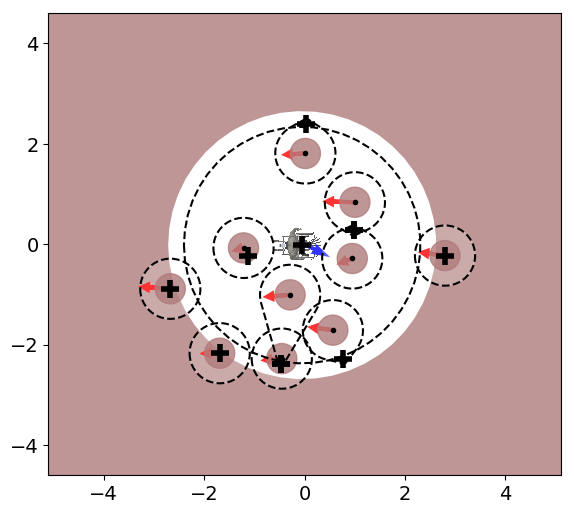
Application to Robotic Arms
The application to multiple degrees of freedom arm can be described and evaluated in joint space. Extending it to a robot that can be encapsulated in a circular shape is done via a constant margin around all obstacles. The danger field is evaluated at multiple evaluation points for each link along the robot arm, and the corresponding weight is calculated. The weights are designed to sum up to one to balance converging and avoiding. The velocity of each joint is evaluated starting at the joint closest to the base of the robot and continuing joint-by-joint towards the end-effector. This allows joints higher up the chain to potentially compensate for the avoidance motion from joints that are lower in the chain.
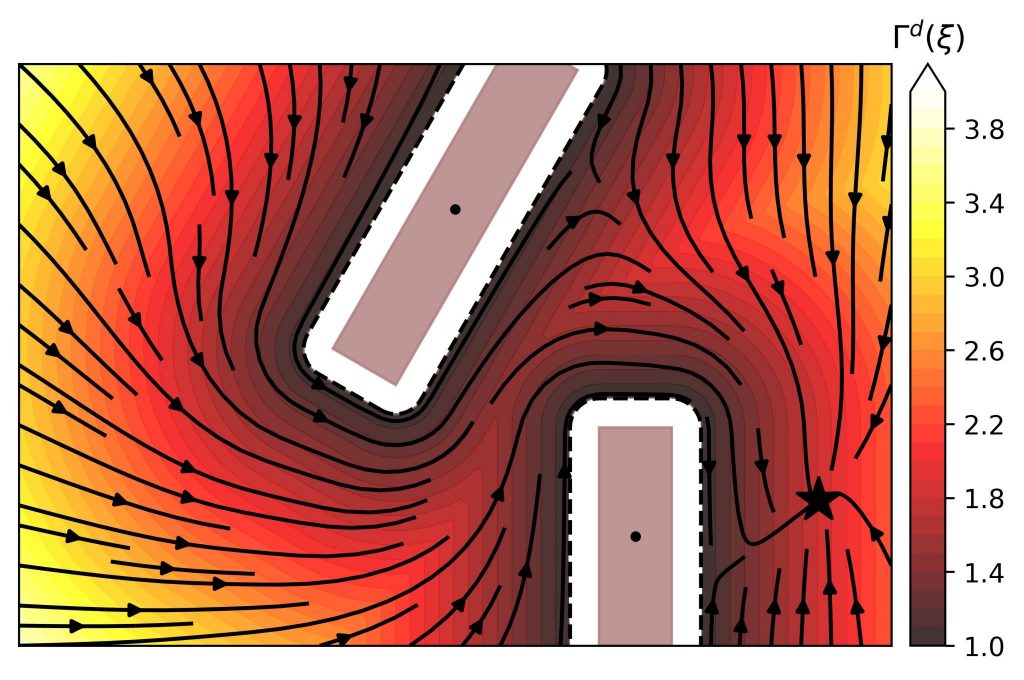
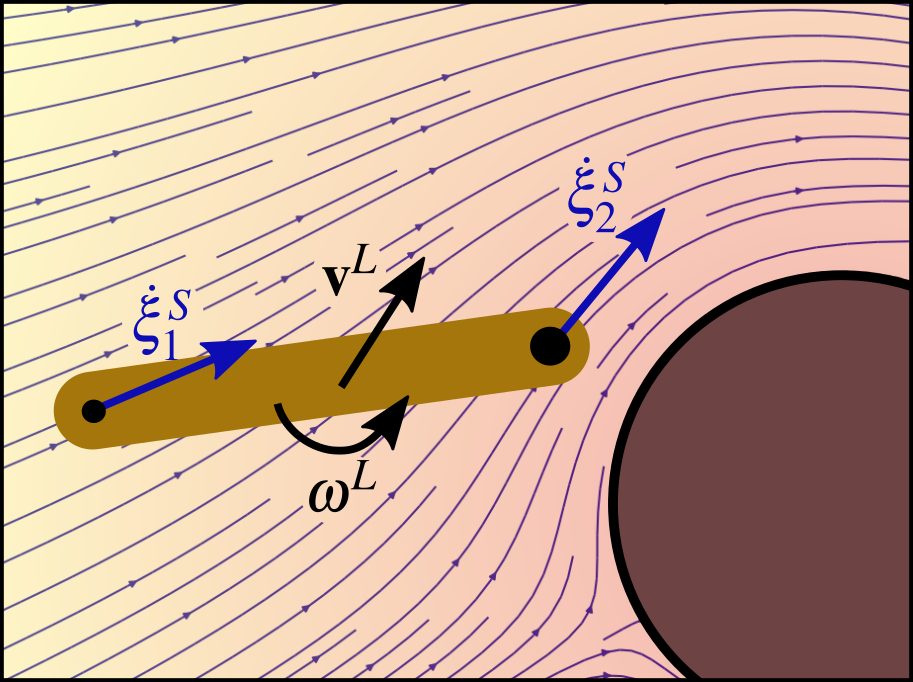
Fast Obstacle Avoidance in Dynamic Environments
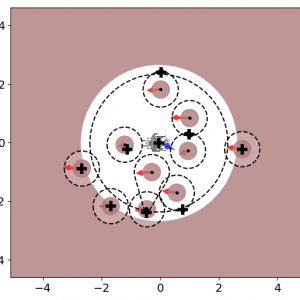
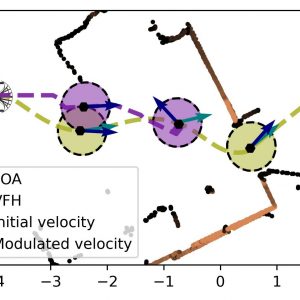
In real-world scenarios, the knowledge of the environment is often just samples of the obstacles, e.g., distance sensors get information about the obstacle in several directions. We have developed a novel avoidance algorithm to treat this sensor data while ensuring collision avoidance in dynamic environments.
We use a concept called modulation. Hence we modulate (or change) the initial velocity, which might be the desired motion of an operator, to obtain a safe, collision-free velocity. Combining mathematical concepts from fluid dynamics and transferring them to robotics ensured a smooth motion that reached each goal.
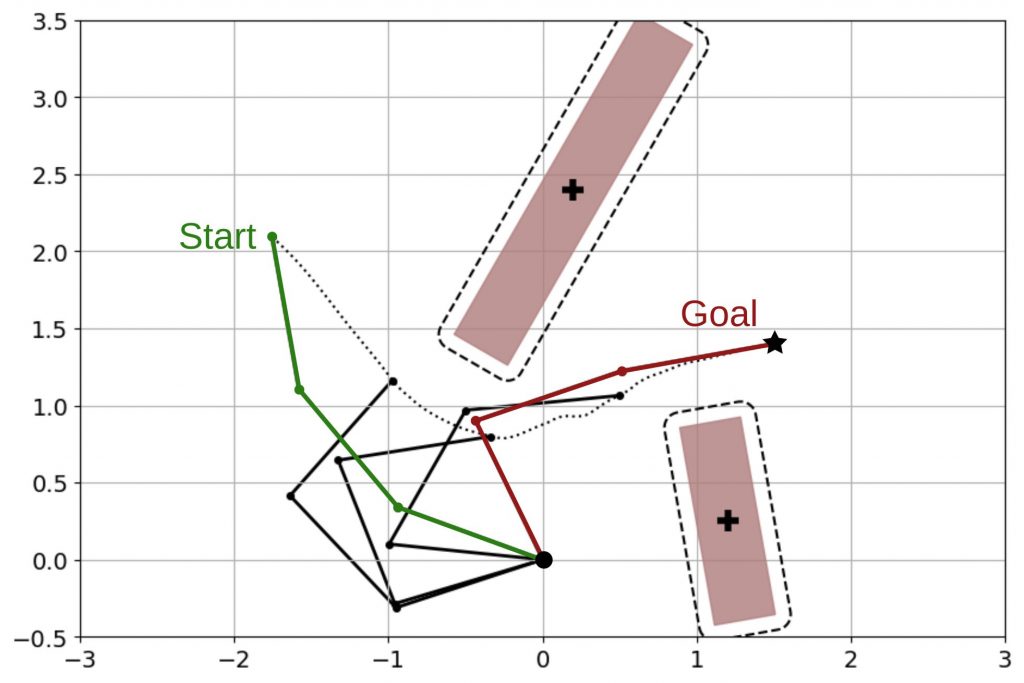
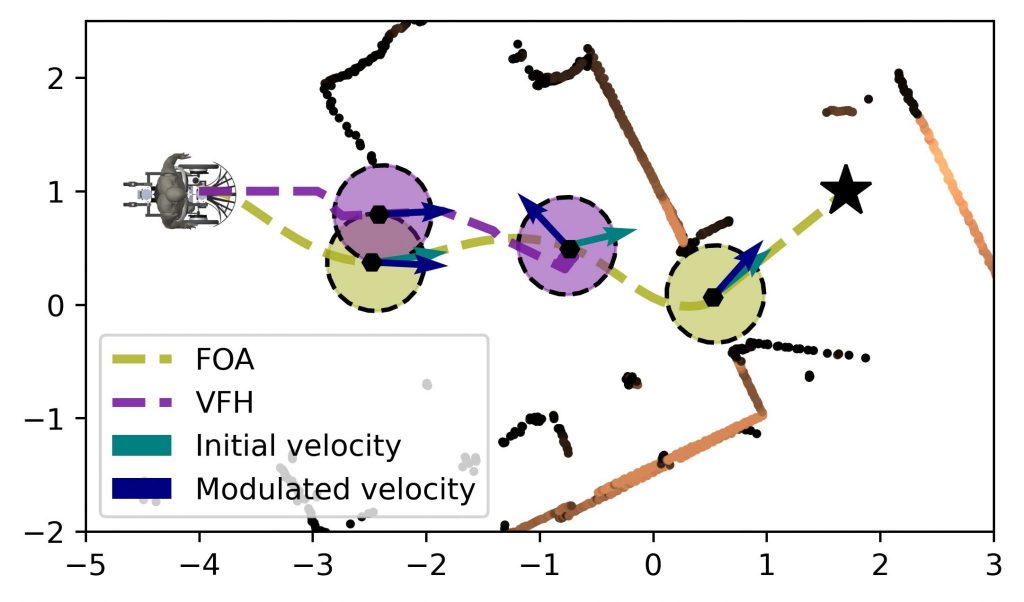
Navigate in Confined and Dynamic Environments
The concepts were applied to shared-control of an operator on a dynamic wheelchair. We compared our new method, called Fast Obstacle Avoidance (FOA), to the existing avoidance method. And were able to show that not only does it allow us to adapt to changes faster, but also more confined environments.

Modeling High Dimensional Demonstrations
This article proposes a novel methodology to learn a stable robot control law driven by dynamical systems. Robots are often required to execute novel tasks that involve convoluted motions in high dimensions. The traditional methods of robot programming to achieve this may require varying levels of user input that may be infeasible and impractical. In these settings, learning from demonstration (LfD) offers an elegant solution to facilitate robot programming and learning novel trajectories for task completion. The goal is to replace the manual process of programming the robot with an automatic programming process whose input consists of demonstration in the ambient space, performed by an expert.
Learning from a single demonstration
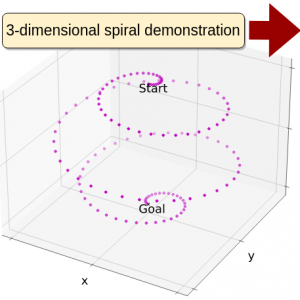
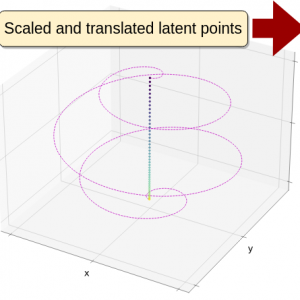
The challenge this paper sets out to address is proposing a data-efficient method to learn a stable control law in high-dimensional ambient spaces by using a single expert demonstration, since it is difficult and expensive to generate a large input data set. The method relies on the idea that there exists a latent space in which the nonlinear dynamics appears quasi linear. The original nonlinear dynamics is mapped into a stable (quasi)linear DS, by leveraging on the properties of graph embeddings.

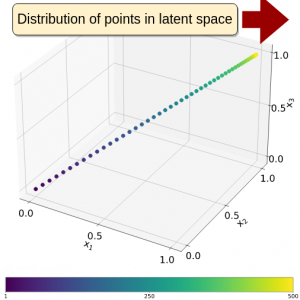
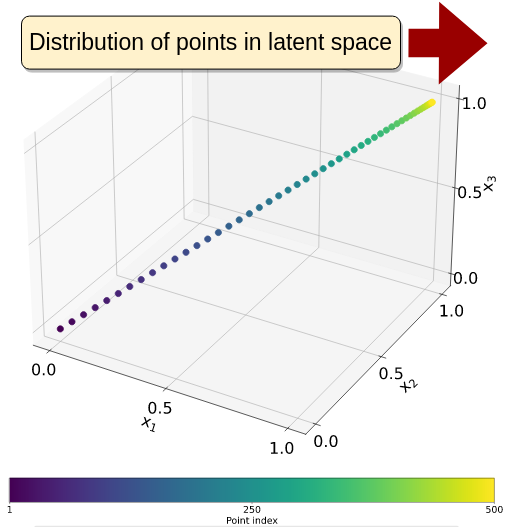
Laplacian Eigenmaps based latent space
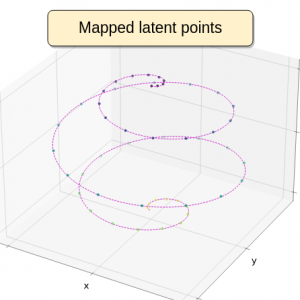
We show that the eigendecomposition of the Graph Laplacian results in linear embeddings in two dimensions and quasi-linear embeddings in higher dimensions. The nonlinear terms vanish, exponentially as the number of datapoints increase, and for large density of points, the embedding appears linear. This new embedding enables to model highly nonlinear dynamics in high dimensions and overcomes alternative techniques in both precision of reconstruction and number of parameters required for the embedding.
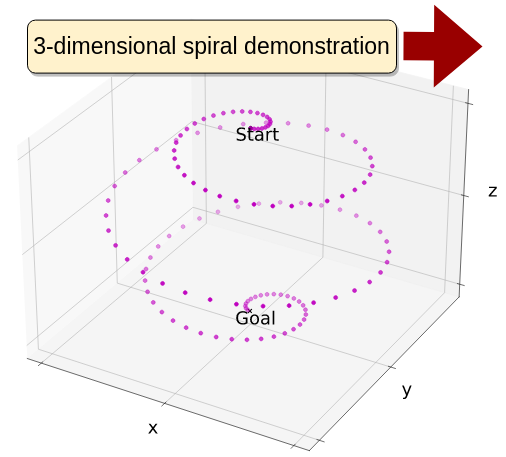
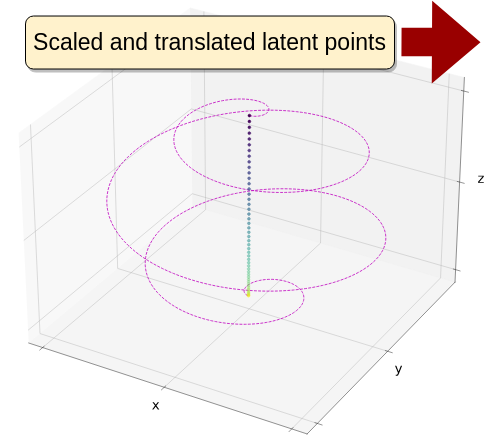
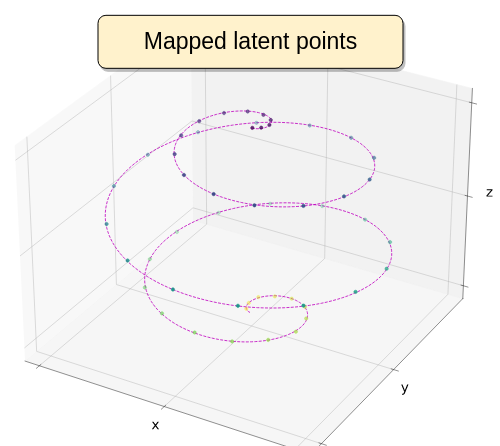
Replication by the learnt DS
We demonstrate its applicability to high dimensional demonstrations by testing with trajectories ranging in dimensionality from 3 to 25. We also perform real robot experiments, by recording kinesthetic demonstrations – both single and dual arm configurations – and learning a DS in joint-space to robustly replicate them, also handling perturbations.





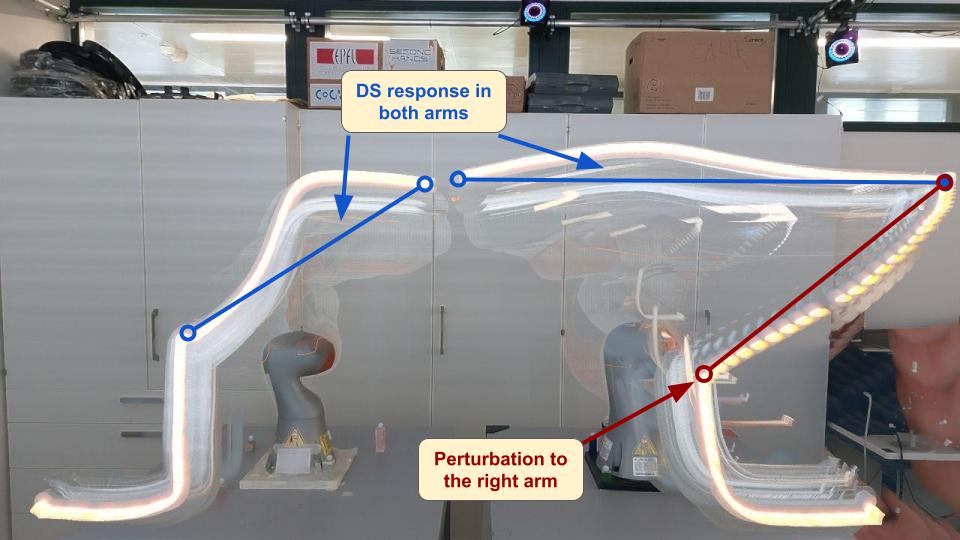

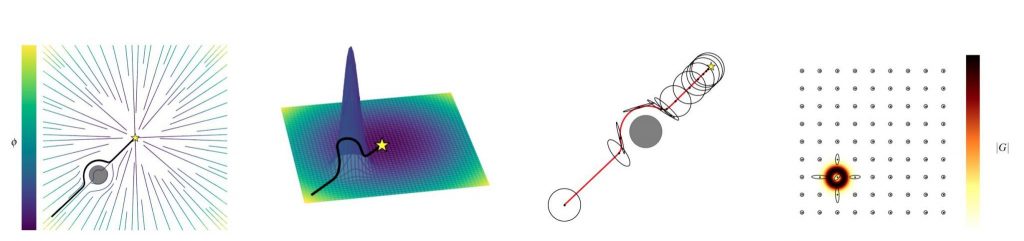
Learning Dynamical Systems Encoding Non-Linearity within Space Curvature

Dynamical Systems (DS) are an effective and powerful means of shaping high-level policies for robotics control. They provide robust and reactive control while ensuring the stability of the driving vector field. The increasing complexity of real-world scenarios necessitates DS with a higher degree of non-linearity, along with the ability to adapt to potential changes in environmental conditions, such as obstacles. Current learning strategies for DSs often involve a trade- off, sacrificing either stability guarantees or offline computational efficiency in order to enhance the capabilities of the learned DS. Online local adaptation to environmental changes is either not taken into consideration or treated as a separate problem. In this paper, our objective is to introduce a method that enhances the complexity of the learned DS without compromising efficiency during training or stability guarantees. Furthermore, we aim to provide a unified approach for seamlessly integrating the initially learned DS’s non-linearity with any local non-linearities that may arise due to changes in the environment. We propose a geometrical approach to learn asymptotically stable non-linear DS for robotics control. Each DS is modeled as a harmonic damped oscillator on a latent manifold. By learning the manifold’s Euclidean embedded representation, our approach encodes the non-linearity of the DS within the curvature of the space. Having an explicit embedded representation of the manifold allows us to showcase obstacle avoidance by directly inducing local deformations of the space. We demonstrate the effectiveness of our methodology through two scenarios: first, the 2D learning of synthetic vector fields, and second, the learning of 3D robotic end-effector motions in real-world settings.
Publications
Khadivar, F., Lauzana, I., & Billard, A. (2021). “Learning dynamical systems with bifurcations.” Robotics and Autonomous Systems, 136, 103700. DOI:10.1016/j.robot.2020.103700.
Huber, L., Slotine, J.-J., and Billard, A. (2022). “Avoiding Dense and Dynamic Obstacles in Enclosed Spaces: Application to Moving in Crowds.” IEEE Transactions on Robotics. DOI
Huber, Lukas, Jean-Jacques Slotine, and Aude Billard. “Fast obstacle avoidance based on real-time sensing.” IEEE Robotics and Automation Letters (2022).
Gupta, S., Nayak, A., Billard, A. (2024). “Learning High Dimensional Demonstrations Using Laplacian Eigenmaps”. Pending submission to IEEE Transactions on Robotics (T-RO)
Fichera, B., Billard, A. , (2024). “Learning Dynamical Systems Encoding Non-Linearity within Space Curvature”. Pending submission to International Journal of Robotics Research.
Huber, L., Slotine, J.J., Billard, A., “Passive Obstacle Aware Control to Follow Desired Velocity”. IEEE Robotics and Automation Letters (RA-L), 2024.
Huber, L., Slotine, J. -J. , Billard, A., “Avoidance of Concave Obstacles Through Rotation of Nonlinear Dynamics”, IEEE Transactions on Robotics, 2023. DOI: 10.1109/TRO.2023.3344034
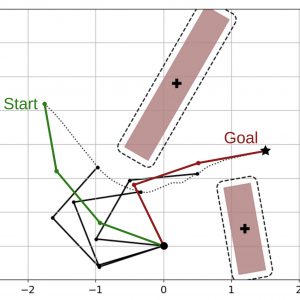
Koptev, M., Figueroa, N., Billard, A., “Reactive collision-free motion generation in joint space via dynamical systems and sampling-based MPC”, International Journal of Robotic research, 2024. DOI: 10.1177/02783649241246557
Khadivar, F., Billard, A., “Adaptive Fingers Coordination for Robust Grasp and In-Hand Manipulation Under Disturbances and Unknown Dynamics”, IEEE Transactions on Robotics, 2023. DOI: 10.1109/TRO.2023.3280028
Fichera, B. and Billard, A. “Linearization and Identification of Multiple-Attractors Dynamical Systems through Laplacian Eigenmaps.” Journal of Machine Learning Research (JMLR), 2022.
Nayak, A., Billard, A., (2024). “Dynamical system approach to navigation around obstacles”. European Control Conference (ECC), June 25-28, 2024 , Stockholm, Sweden.
Fichera, B., Billard, A. (2023). “Hybrid Quadratic Programming – Pullback Bundle Dynamical Systems Control .”, 8th International Symposium of Robotics Research (ISRR), Sep 25-30, 2022, Geneva, SWITZERLAND.
Huber, L, Slotine, J.-J., and Billard, A. (2021). “A Unified Approach to Obstacle Avoidance and Motion Learning.” Workshop on Deployable Decision Making in Embodied Systems (DDM). NeurIPS 2021.