The Laue Condition for Diffraction and The Ewald Sphere
Nicolas Schoeni and Gervais Chapuis
École Polytechnique Fédérale de Lausanne, Switzerland
The Laue Condition for Diffraction
From the Reciprocal Lattice Generator application, we can learn that each reciprocal lattice vector h is an integer combination of the three reciprocal basis vectors a*, b* and c*:
where the triplet of integers (h, k, l) characterizes uniquely each reciprocal lattice vector.The recipocal lattice vectors a*, b* and c*can be derived from the lattice vectors a, b and c from the vector products
where V is the volume of the unit cell defined by the vectors a, b and c.
It is convenient to introduce the vector s0 which is parallel to the direction of the incident beam. Its magnitude is set as the inverse of the wavelength λ of the incident beam:
Similarly, the direction of the diffracted beam is described by the vector s with its magnitude
The Laue condition states that the following equality must be fulfilled:
for diffraction to occur.
The Ewald Sphere
The Laue condition requires that the three vectors s0, s and h must form a triangle with two identical sides:
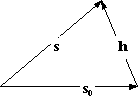
If a sphere is constructed with the center at the origin of s0 and |s0| as radius, the diffracting conditions are satisfied only if the endpoint of a reciprocal lattice vector h is located on the surface of the (Ewald-) sphere. The direction of the diffracted beam is than given by the direction of the vector s. By changing the orientation of the reciprocal lattice relative to the incident beam s0, each vector h which cuts the Ewald sphere gives rise to a diffracted beam which is parallel to the direction of the corresponding vector s.

Based on the Ewald sphere, it is clear that each reciprocal lattice vector can only give rise to a diffracted beam if the reciprocal lattice takes successively different orientations. This means that with a monochromatic beam, i.e. a unique wavelength, the crystal has to be moved relative to the incident beam in order to generate diffraction peaks. For a complete measurement of all the accessible diffraction intensities, the crystal must be displaced so that each reciprocal lattice vector satisfies the Ewald conditions.
To illustrate this point further, we offer an animation of a simple lattice rotating through an Ewald Sphere:
The white beam in this animation is the incident beam and the yellow beams are the diffracted beams. For didactical reasons, the origin of the diffracted beam has been placed at the center of the Ewald sphere. In practice, the diffracted beam originates from the diffracting crystal, i.e. from the origin of the reciprocal lattice.