Crystallography applets and simulation
This page is dedicated to the teaching of crystallography and was developed at the EPFL in Lausanne (Switzerland).
It was first developed by Wes Hardaker and further extended by Nicolas Schoeni under the responsibility of Prof. G. Chapuis.
Recently, all the applets have been updated in 2016 by Nicolas Casademont et Maria Sisto.
You will find applets dedicated to the three basic topics of crystallography, namely symmetry, diffraction and structure solution algorithms.
The symmetry applets range from learning the concept of point group symmetry, getting familiar with the symmetry of periodic objects in two dimensions, and also learning about the space group concept for the description of crystalline structures in 3D. An additional applet will help you in finding the new atomic coordinates of a new unit cell provided the matrix transformation from the original unit cell to the new one.
For diffraction, a simple animation of Bragg’s law will help to find the constructive interferences depending on the diffraction angle. Another applet will teach how to obtain the reciprocal lattice based on the original unit cell. Two applets illustrate the concept of Ewald sphere in order to understand the diffraction principles and simulate various diffraction methods. The user will be able to play with the concept of Fourier transform to generate the crystalline structures on the basis of diffraction patterns. From any CIF file (a crystallographic standard to describe atomic structures), the user will be able to simulate either powder or single crystal diffraction patterns.
Finally, the concepts of the Patterson function and the charge flipping algorithms are illustrated for a better understanding of the phase problem in crystallography.
Most of the applets are written in Java and need to be downloaded. For technical reasons, the JAR files are stored inside ZIP archives.
- For these applets to work you must have the Java Runtime Environment 7 (Java 8 seems to work too) installed on your computer. If you don’t have it you can download it here: JRE 7 download.
- To download the applets click on the download links below. We provide support for most usual systems: Windows 32/64 bits, macOS, Linux 32/64 bits. If you are having any trouble making the applet work contact Prof. G. Chapuis.
It appears that the latest versions of Java are not compatible with the crystallographic applets using 3D representations.
The problem can be solved by downloading an older version of JRE, namely, jre-10.0.2_osx-x64_bin.dmg. The JRE will get installed in folder Library → Internet Plus-ins.
When running the applet for the first time, some security issues might happen. In this case go to Preferences → Security and Confidentiality → General and give the permission to run the JRE.
1. Symmetry
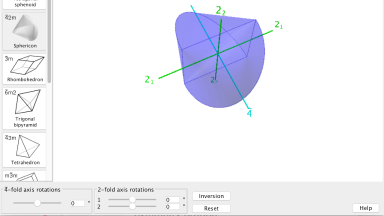
Discovery of point group symmetry groups
An applet to explore the point group symmetry of platonic and other polyhedra. In particular, rotations, inversion and combinations of them can be simulated.
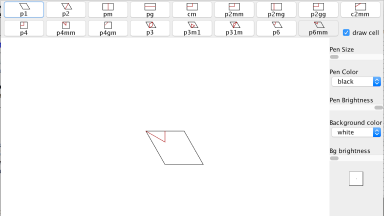
Escher Web Sketch 2
An applet to simulate any periodic pattern corresponding to one of the 17 possible two-dimensional symmetry groups (17 planar groups).
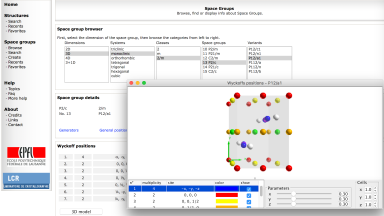
Crystallographic Symmetry Environment (CSE)
A series of tools to visualize among others the Wyckoff positions of each space group in 3D.
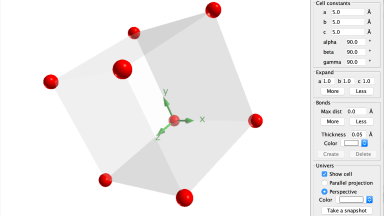
CrystalOgraph
An applet to represent any type of crystalline structure given the lattice parameters, the space group and the atomic coordinates of symmetry independent atoms. It is also possible to import directly a structure from the ICSD database or from a CIF file.
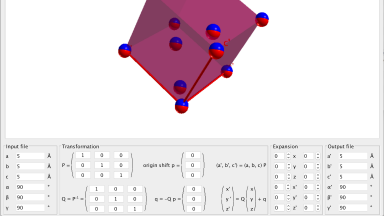
CellConverter
An applet to transform any unit cell ant its content to another cell. Based on the original CIF file, the applet generates a new CIF file resulting from the transformation specified by the user.
2. Diffraction
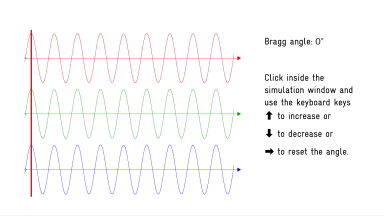
Bragg scattering
A Flash animation to illustrate constructive or destructive interferences as expressed by Bragg’s law.

Reciprocal lattice generator
From a periodic diagram generated by Escher Web Sketch, the user is guided step by step by the applet in order to create the reciprocal lattice corresponding to the periodicity of the initial periodic pattern.
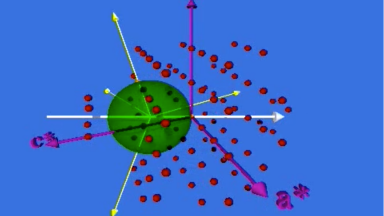
Ewald sphere animation
Video sequence illustrating the diffraction phenomenon based on the Ewald sphere.
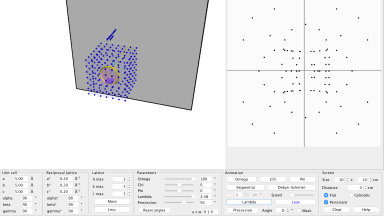
DiffractOgram
An applet to simulate any type of diffraction pattern based on the Ewald sphere and the reciprocal lattice. In particular, Laue patterns, Debye Scherrer diagrams, rotating crystals and even precession photographs can be generated.
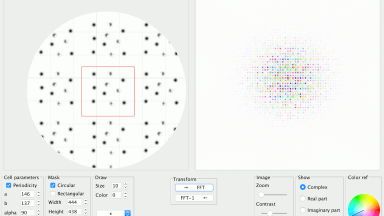
Diffraction and Fourier Transform
An applet to calculate the Fourrier Transform of a density function ρ(x) yielding the complex magnitude G(S). The density function can be either periodic or non-periodic. The applet is also able to calculate the inverse Fourier transform of G(S). Numerous tools can be applied in order to understand the role of amplitudes and phases, which are of particular importance in diffraction phenomena.
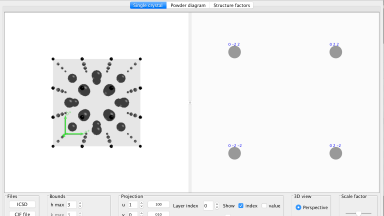
ReciprOgraph
An applet to simulate the X-ray diffraction intensities for single crystal in reciprocal space and powder diffraction patterns. Structures can be selected from from CIF files.
3. Structure resolution
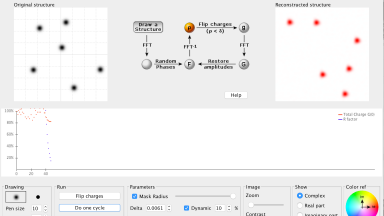
Charge Flipping
An applet to solve the phase problem in diffraction by the charge flipping algorithm. The user can create a 2D crystalline structure and follow the evolution of the algorithm in solving the structure.