Aim
 |
Provide DSOs and power suppliers with tools for the planning and operation of utility scale and distributed battery energy storage systems, in order to optimize the integration of distributed generation. |
Activities
Feeder operational limits
The activity aims to study the operational limits of the electrical distribution feeders of an urban and an rural areas. Rolle was considered as a urban area and Onnens as rural one. For this purpose, a Probabilistic Load-Flow approach was used which accounts for the stochasticity associated with loads/injections by considering that these quantities are represented by probability density functions (PDFs) at a given time interval. This allows for a probabilistic assessment of the associated stochastic network state.
The first step toward performing a PLF analysis is to infer the statistical distribution, namely the PDFs for the different periods of the day/month/season/year, of the loads and injections in the network. The statistical distributions of the network states were obtained by using a numerical approach based on Monte Carlo simulations. A large number of values of loads and injections were sampled from the corresponding distributions and a deterministic load flow was solved for each combination of these values. For the specific case of Onnens, the seasonal and cloudy/clear sky PV’s PDFs, and seasonal and weekday/weekend load PDFs were considered. The historical data of the parameters (load active/reactive power consumptions and solar irradiation) are collected from RE and empirical measurement at the EPFL-DESL.
Sizing and siting of BESS
For the optimal steering with a use of a Battery Energy Storage System (BESS) of a grid within the safe operation limits for both node voltages and line currents, both size and location of the BESS should be defined.
In this respect, a newly proposed Augmented Relaxed Optimal Power Flow (AR-OPF) model was used as the core of the optimization model to optimally locate and size a suitable energy storage system composed by a utility-scale battery.
The AR-OPF takes into account the correct model of the lines and the network security constraints related to the nodal voltage magnitudes and lines ampacity limits. Sufficient conditions are identified to guarantee that the solution of the AR-OPF formulation is feasible and optimal.
By using the AR-OPF method, a specific optimization problem associated to the optimal resource, particularly the BESS, planning and operation in ADNs. The objectives set includes minimization of (1) nodal voltage-magnitude deviation (2) lines’ congestions, and (3) nodal voltage fast fluctuations.
Operation of the BESS for grid control
The use of BESSs for the provision of only one service may or may not need, on a daily basis, their full capacity. This depends on the daily operational conditions such as weather, variability of grid’s frequency etc. In order to avoid “wasting” available capacity and to exploit optimally these assets, multiple services can be provided in parallel. Therefore, a control framework is developed for a BESS to, simultaneously, a) dispatch the operation of an active distribution feeder and b) provide primary frequency regulation (PFR) to the upper grid layer.
Every 24 hours, we solve a robust optimization problem. According to this problem, we identify a dispatch plan for the next 24 hours and the amount of power to provide the primary frequency regulation so that the exploitation of the BESS energy capacity is maximized. Also, the BESS energy and power limits shall be respected at any time in the next 24 hours and in the case of any scenario of feeder load and frequency deviation. These two pieced of information are then used in the BESS real-time control. In this phase, the power set-points for the dispatch and frequency regulation are computed independently and superimposed (Namor et al, 2018).
Dynamic grid model for distributed controller strategy
A novel data-driven, robust control design method was developed for decentralized device-level as well as distributed primary/secondary control. A frequency-domain modeling approach (Figure 1) is used to describe the transient dynamics of the grid. Unlike classical modeling techniques, the obtained transfer function models are well suited for control design. The same approach can be applied for dynamic phasor modeling of power flows, and the model also allows for sensitivity analysis (Kammer & Karimi, 2017).
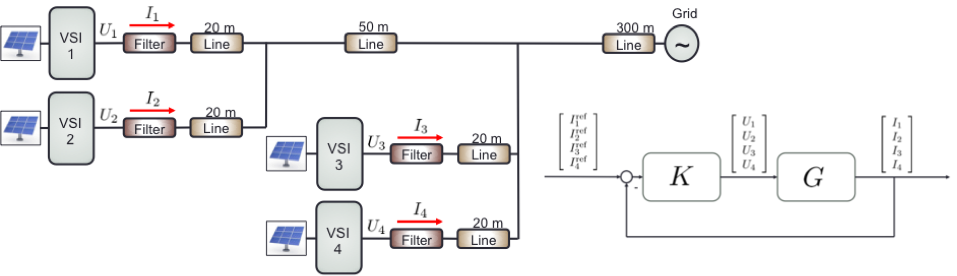
Figure 1: Frequency-domain modeling approach to describe grid dynamics and transfer function representation.
Ancillary services to the upper grid
This project is carried out in two stages. The first stage investigates the project from Transmission System Operator (TSO) perspective. It determines the required ancillary services from Regional Energy Networks (RENs) by TSO while modeling the RENs ideally. This means that they can provide ancillary services to the transmission system as far as the rated power limit of the substations connecting them to the transmission is not violated. The second stage investigates the project from DSO perspective. It determines the actual capability of each individual REN for provision of ancillary services to the transmission system by considering all flexibility resources located in it.
Aging analysis of the BESS
In 2017, the aim of this activity was to develop ageing models that allow the aging/cost analysis of the usage of a battery with specific chemistry and nominal parameters. As a next step, the models will be further improved based on additional data; and used to analyse the operation of the BESS in rural test are and provide its aging profile. The outcomes could be used for the reduction of the BESS ageing during operation, while keeping the discharged energy (and therefore economic benefits) at the same level (Torregrossa, et al, 2017).
Preliminary Results
Feeder operational limits
For the statistical characterization of the network nodal injections from loads and PV, it is assumed that the aggregate load or PV plant at the kth time interval of the day denoted hereafter by Lk is a random variable. The time aggregation horizon to perform the PLF is of 15 minutes. For each time interval, the available samples are observed after removing the outliers and the mean ((?k−?̅k). The QQ-plot of the zero-mean data for a specific time interval for a load in Onnens in winter are shown in Figure 1.
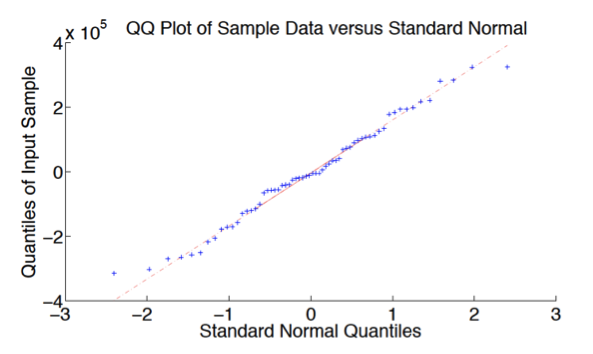
Figure 1: QQ-plots of zero-mean data for a load in the network. Data obtained for a specific time interval (15 minutes) of the day during the winter period. The dataset to infer this kind of plots is of 91 days
Temporal correlation of the random vectors ??,?=1,…,96 was taken into account. In this respect, it was assumed that the random vector (?−?̅)=(?1−?̅1,…,?96−?̅96) follows a multivariate Gaussian distribution (?−?̅)=?(0,Ω) where Ω is the covariance matrix that contains the whole information about the variance and covariance of the random variables (??−?̅?,?=1,…,96). The obtained distributions are used to generate scenarios using multivariate normal random numbers for each temporal bin.
Given that in the feeder there is one PV injection, the available data were used to generate the CDF used in the Monte Carlo simulation. The specific profiles of yearly aggregated load consumption and PV production that were used to infer the multivariate statistical distributions are presented in Figure 2.
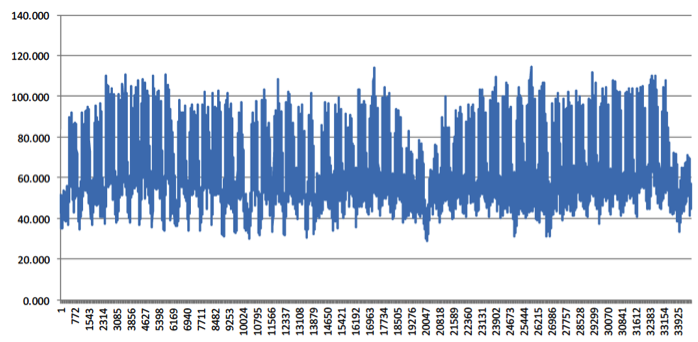
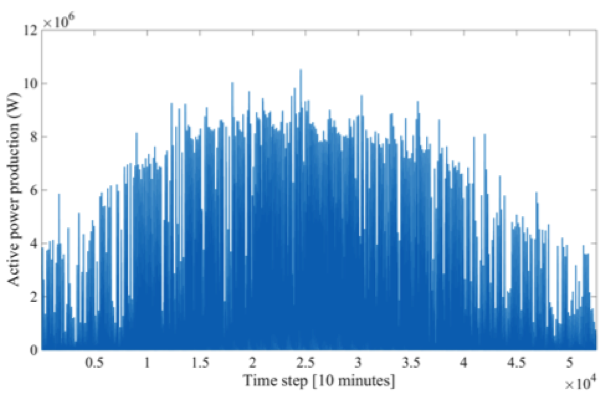
Figure 2: Yearly aggregated load consumption (up) and PV production (bottom) for the feeder. The data of the PV production has been generated using meteorological information of the irradiance, a transposition model of the PV panels and their model derived from DESL experience
The PLF was used to assess the steady-state security of the grid. The obtained Cumulative Distribution Function (CDF) of the nodal voltage-magnitudes and lines’ current for all the network nodes and lines are clustered for the four seasons of the year as illustrated on the Figure 3 and Figure 4.
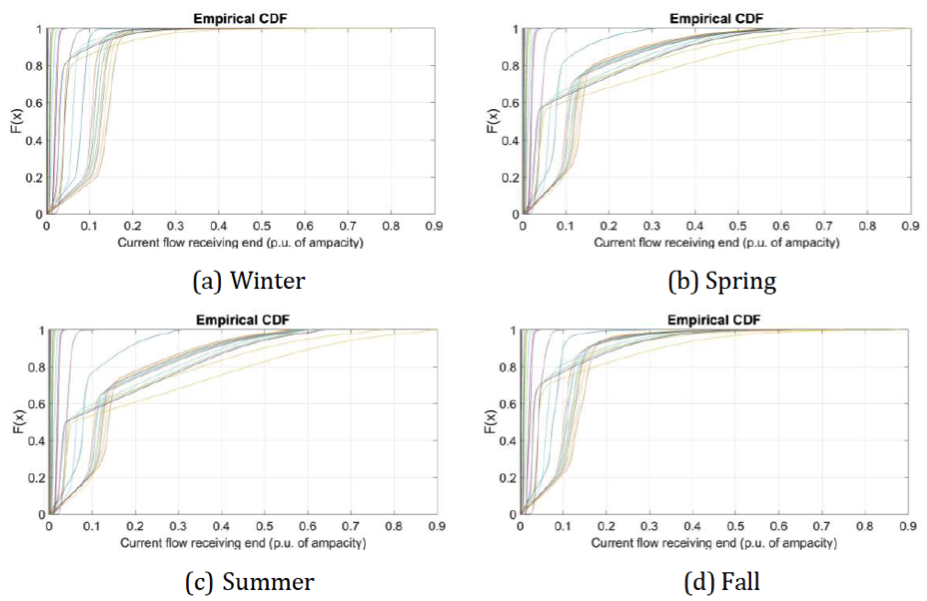
Figure 3: CDF of the lines’ current of the medium feeder
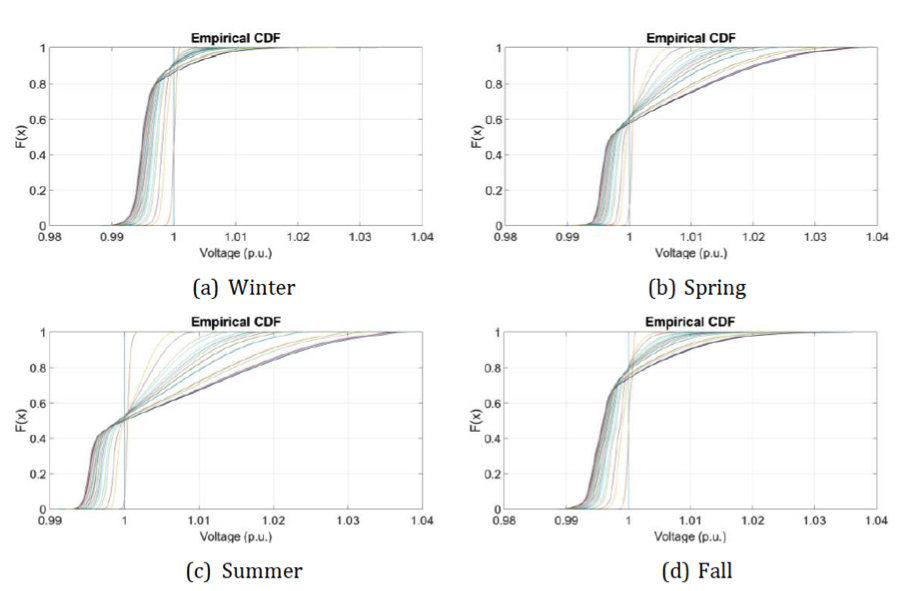
Figure 4: CDF of the nodal voltage magnitudes for feeder
As illustrated, the feeder faces over-voltages in 3 seasons: summer, spring and fall while the network lines operate close to their ampacity limits during spring and summer periods.
The second grid is composed by six low voltage systems on the site of Rolle. The lines’ current and nodal voltage-magnitudes of all the six low voltage grids are within the safe operational margins for all the simulated scenarios. Therefore, their analysis not reported here. The outcome of this analysis about the Rolle’s low votage power grids, allows to conclude that the controls deployed in this part of the demonstrator, do not need to account for the grid operational constraints. (Christakou et al, 2017)
Sizing and siting of BESS
This methodology has been applied in a test area, in Onnens, where the feeder is expected to face over-voltages and lines’ congestion when the 8.5 MW PV plant is fully operational.
Τhe model implementation resulted to the optimal location and size of the battery. The former is illustrated on the Figure 5 and the later is the following:
- Energy reservoir (MWh): 3 (for the local grid control) + 1.8 (for achieving the dispatchability of the feeder)
- Power rating (MVA): 3
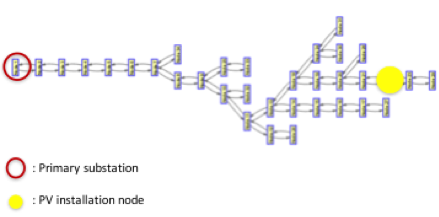
Figure 5: Topology of the 20kV feeder and identification of the optimal location of the BESS based on the model implementation
The effect of the BESS on the feeder voltages and line currents was studied by analysing the feeder behavior when the PV injection is maximized and the expected load minimized. This assessment is performed with a simulation time step of 15 minutes.
The following results were observed (see Figure 6):
- nodal voltage-magnitudes: <1.2 p.u.
- lines’ current: <90% of their respective ampacity limit
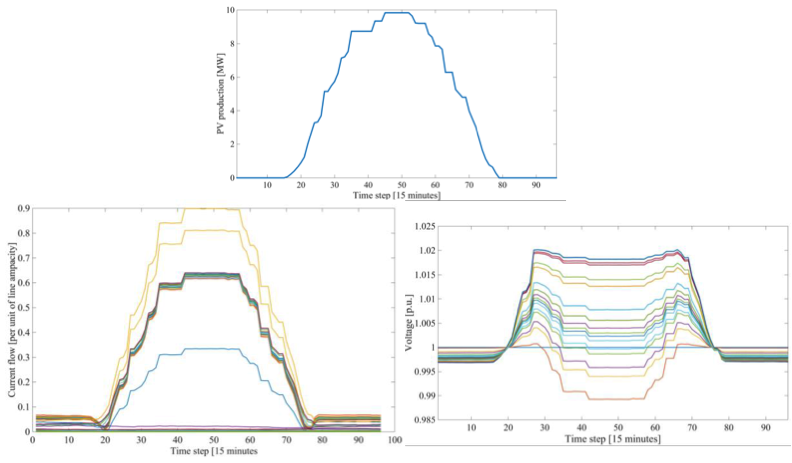
Figure 6: Highest expected PV injection in summer for the test feeder (top); Profiles of the node voltage magnitudes of the test feeder for these PV injection (bottom right); and Profiles of the lines’ current flow (in per unit of their respective ampacity) of the test feeder for these PV injection (bottom left)
Furthermore, the effect of the BESS on the test feeder voltages when there is fast voltage fluctuation due to rapid changes of the PV output was studied. A high-resolution (1 second) irradiance time series measured at the EPFL-DESL during a partial cloudy day was used and transformed in the power injection of the PV plant connected to the test feeder. The Onnens note voltage profiles with and without the action of the BESS are shown on the Figure 7 (Nick and Paolone, 2017).
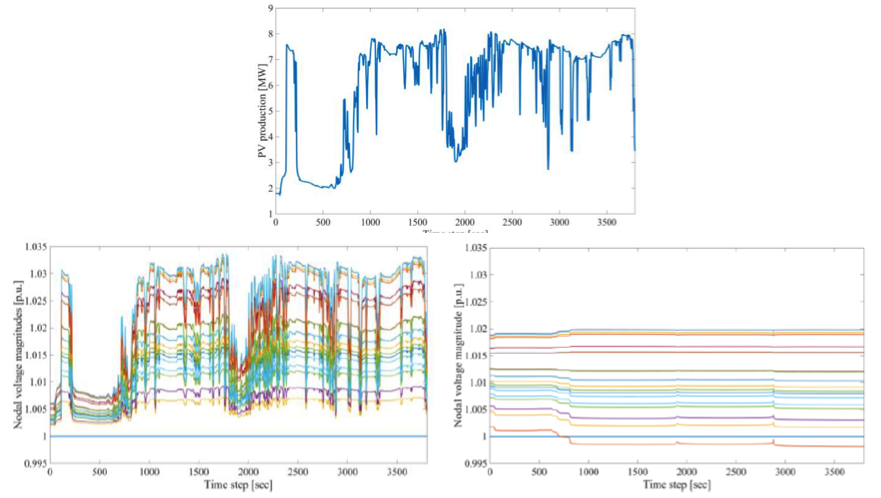
Figure 7: Profile of the fluctuating PV injections that might take place in the test feeder (top); Onnens node voltages obtained with the PV profile high intermittent PV output (each plot shows the profile for one node) without (bottom left) and with BESS (bottom right)
Operation of the BESS for grid control
This framework was tested on the 560 kWh installed at the EPFL campus and the BESS state of charge and power remain within adequate limits. Figure 8 shows these quantities during one day of operation.
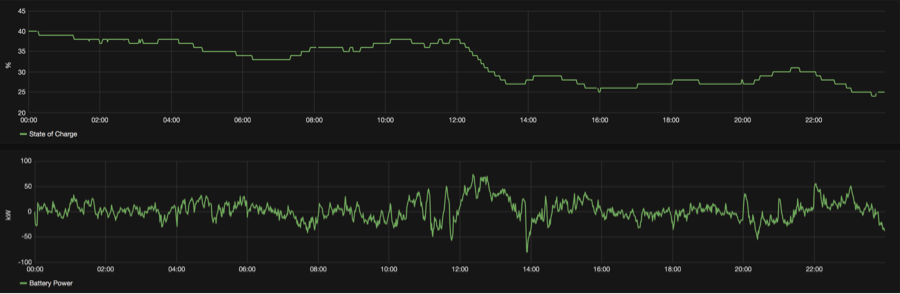
Figure 8: State of charge (top) and power (bottom) of the 560 kWh BESS installed at the EPFL campus
Long-term simulations of the proposed framework were performed. Figure 9 shows the stored energy during one month of simulation. The key outcomes are (Sossan et al, 2017):
- The capacity made available for dispatch and PFR corresponds every day to the full BESS capacity.
- The power provided to the PFR (red dots in the Figure 9), varies daily as a result of our optimisation problem
- We do not perform PFR in those days in which the uncertainty on the load forecast is too high (see for instance day 15, 19 and 20)
- We are able to manage to BESS state of energy so to achieve uninterrupted operation
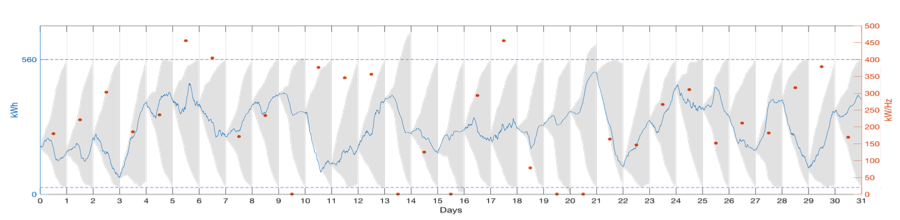
Figure 9: Simulation of the proposed framework
Dynamic grid model for distributed controller strategy
In 2017, parametric models were developed and validated in simulation. Based on these models, device-level and distributed primary/secondary robust control design has been demonstrated and validated in simulation. PHIL experiments of a current controller prove the usefulness of the approach in a realistic setup (see Figure 10).
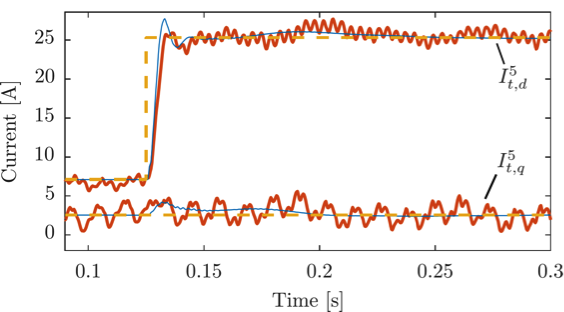
Figure 10: Performance evaluation in PHIL experiments of the current controller
Ancillary services to the upper grid
Until today, in regard to the first stage, a generic modeling framework for power system including RENs and generating companies units (GENCO-Units) was developed with the aim of providing frequency control services (FCSs) to the transmission system, as shown in Figure 11. Based on the proposed modeling framework and relying on a DC power flow model, the problem was formulated as a linear scenario-based stochastic optimization problem consisting on minimizing the cost of FCSs provision and deployment from all possible providers including RENs and GENCOs. Nodal and total Expected Load Not Served (ELNS) indices were used to measure the security of the transmission system against the scenarios. Finally, the IEEE 24-bus test system was considered as a case study to evaluate the effectiveness of the proposed approach.
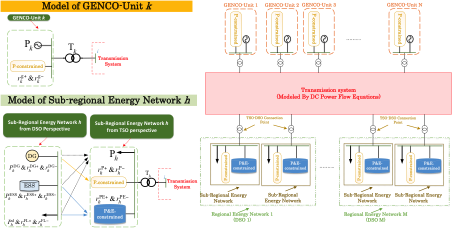
Figure 11: TSO-Perspective: Dimensioning the required active power reserve by TSO
The achieved results indicate that the proposed approach can help TSOs by giving them a clear perspective about their optimal needs to FCSs from different RENs or GENCOs.
Moreover, a preliminary framework was proposed for the second stage. The second stage of this project is a complex problem because it includes a large number of flexibility resources with different sizes and networks with different voltage levels and different characteristics (X/R) leading to a probable ill-conditioned network admittance matrix.
In order to mitigate the complexity of the problem, a hierarchical bottom up approach is adopted and the problem is decomposed into two sub-problems based on the general structure of the RENs, as shown in Figure 12. The first sub-problem, entitled ADN level optimization, determines the capability of each ADN located in the RENs. The second sub-problem, entitled sub-transmission level optimization, determines the capability of sub-transmission system (consequently RENs) considering the outputs of the first sub-problem.
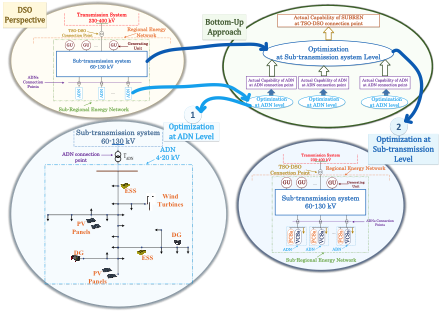
Figure 12: DSO-Perspective: Actual Capability of Regional Energy Networks for Provision of Ancillary Services
For the analysis of the aging process of BESS, numerical models have been developed. These are tailored to different battery chemistries such as LFP, NMC, and LTO, based on empirical data from research conducted by universities, research centers and battery manufacturers. The models are taking into consideration key factors that affect non-linearly the capacity loss over time namely C-rate (charge/discharge); Depth of Discharge (DoD); and Temperature. Moreover, the impact of C-rate on cycle efficiency (Peukert’s effect) and the capacity degradation for the updated DoD computation were integrated in the aging models.
Involved partners/Contacts
 |
BESS operation: Dr. Fabrizio Sossan (EPFL-DESL) Distributed contoller: Christoph Manuel Kammer (EPFL-LA) Ancillary services: Mohsen Kalantar Neyestanaki (EPFL-PWRS) |
References
Christakou, K., Nick, M. and Paolone, M. (2017) Study of targeted feeders’ (Onnens/Rolle) operational limits. REel Demo deliverable
Namor, E., Sossan, F., Cherkaoui, R., & Paolone, M. (2018). Control of Battery Storage Systems for the Simultaneous Provision of Multiple Services. IEEE Transactions on Smart Grid, (accepted for publication). https://infoscience.epfl.ch/record/253397?ln=en
Nick, M and Paolone, M. (2017) Sizing and siting of a utility scale distributed battery energy storage system (Romande Energie Demonstrator). REeL Demo deliverable
Sossan, F., Namor, E., and Paolone, M. (2017) Operation of the battery storage systems for grid control, feeder dispatching. REeL Demo deliverable
Kammer, C., & Karimi, A. (2017). Decentralized and distributed transient control for microgrids. IEEE Transactions on Control Systems Technology. https://infoscience.epfl.ch/record/228979?ln=en
Torregrossa, D., and Niederhäuser, E.L., (2017) Rooftop Photovoltaic Power Plant and Electrochemical Storage: Trend and Perspectives for Residential Buildings. In: ICESEE. October 2017, Budapest, Hungary. IEEE. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8294157