| Type | Master project |
| Split | 50% theory, 50% software |
| Knowledge | Programming skills (C++/ Python) |
| Subjects | Differential Geometry, Machine Learning, Robot Planning, Control Theory, |
| Supervision | Bernardo Fichera, Farshad Khadivar |
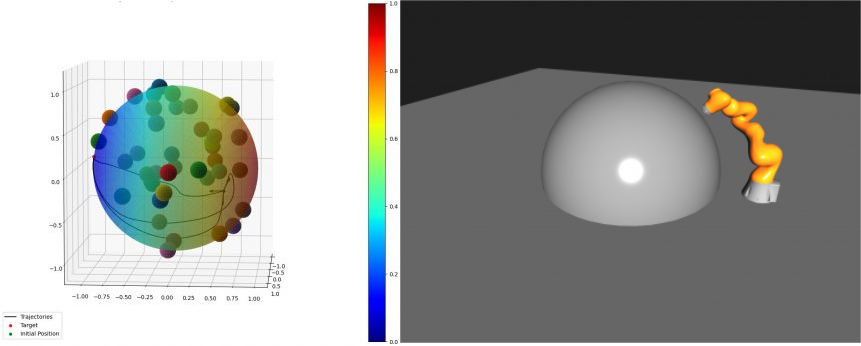
Dynamical System (DS) – based closed-loop control is a simple and effective way to generate reactive motion policies that well generalize to the robotic workspace while retaining stability guarantees. Lately, formalism has been expanded in order to handle arbitrary geometry curved spaces, namely manifolds, beyond the standard flat Euclidean space. Despite the many different ways proposed to handle DS on manifolds, it is still unclear how to apply such structures to real robotic systems. In this preliminary study, we propose a way to combine modern optimal control techniques with a geometry-based formulation of DS. The advantage of such an approach is two fold. First, it yields a torque-based control for compliant and adaptive motions; second, it generates dynamical systems consistent with the controlled system’s dynamics. The salient point of the approach is that the complexity of designing a proper constrained-based optimal control problem to ensure that dynamics move on a manifold while avoiding obstacles or self-collisions is “outsourced” to the geometric DS. Constraints are implicitly embedded into the structure of the space in which the DS evolves. The optimal control, on the other hand, provides a torque-based control interface and ensures the dynamical consistency of the generated output. The whole can be achieved with minimal computational overhead since most of the computational complexity is delegated to the closed-form geometric DS.
Approach
Coming up…
Expectation
Coming up…
References
Coming up….