Elastic Knots
A deployable structure built from a multistable elastic knot
- Project Overview
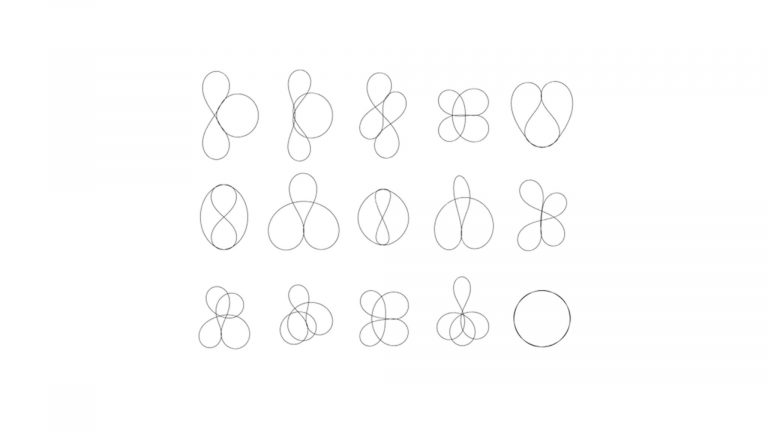
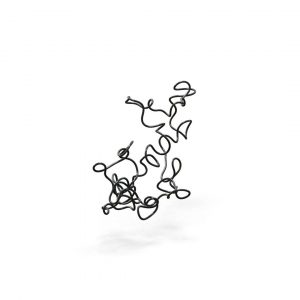
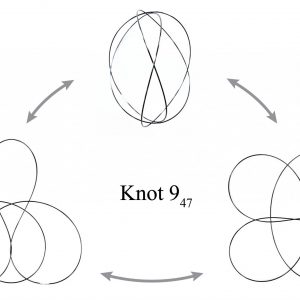
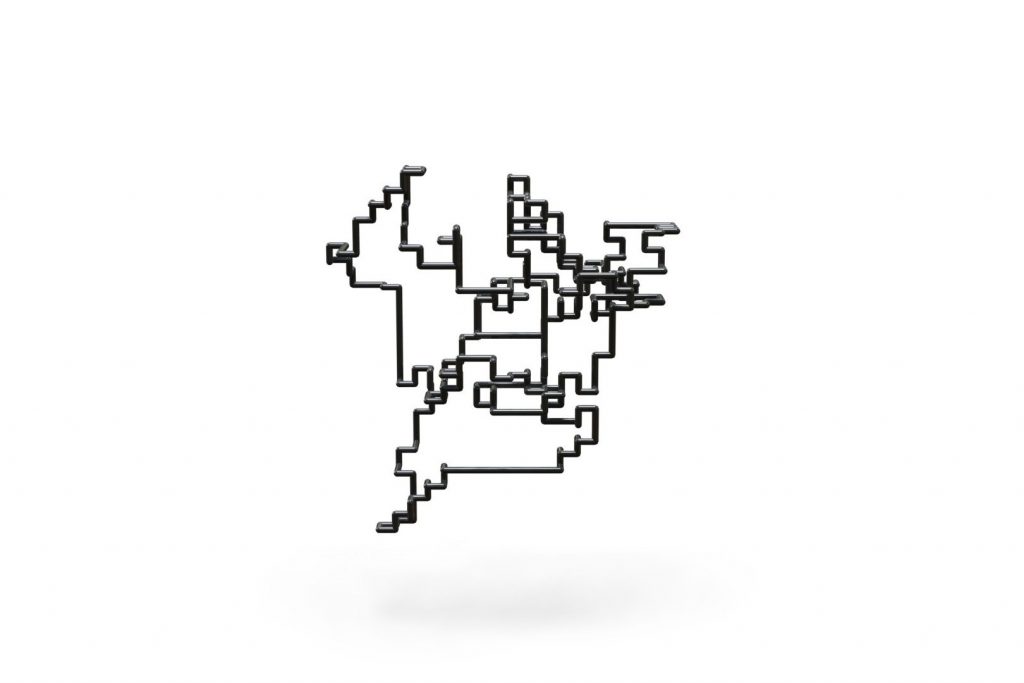
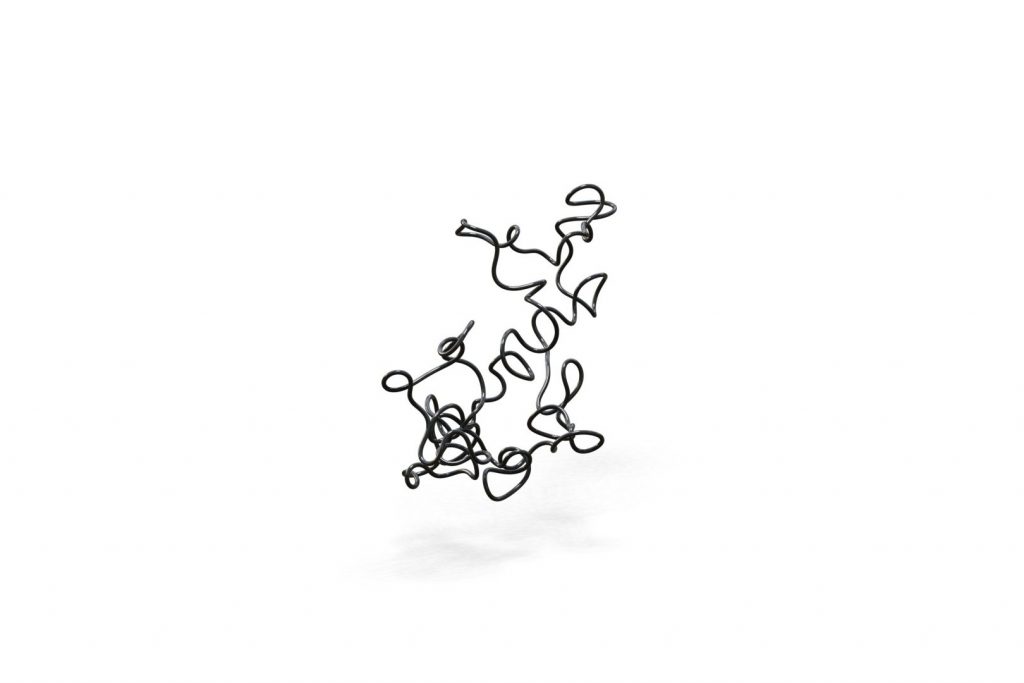
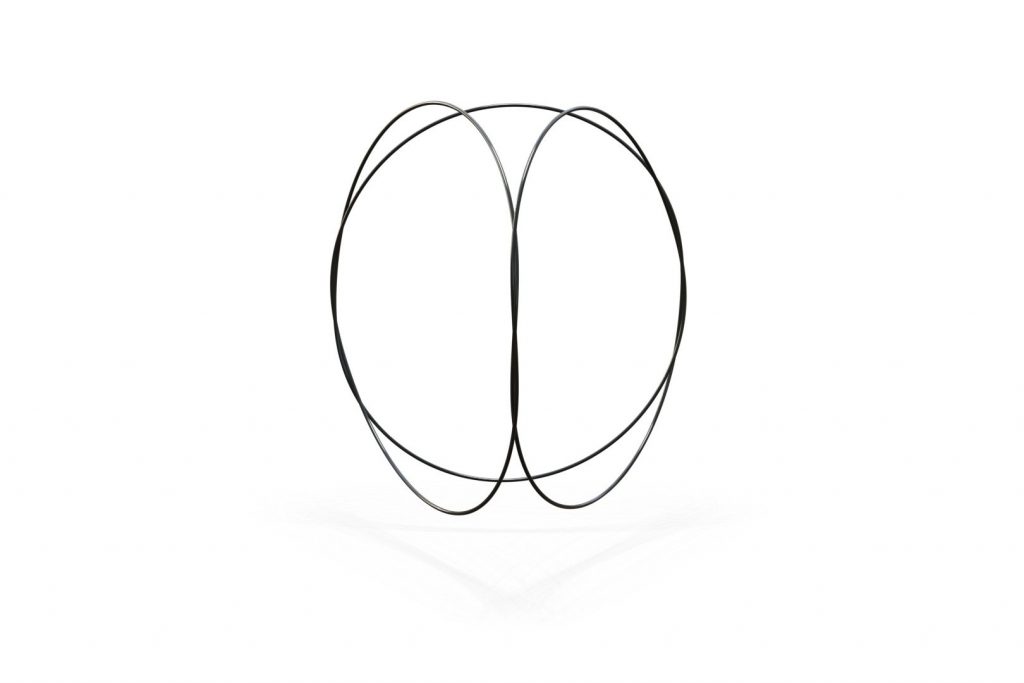
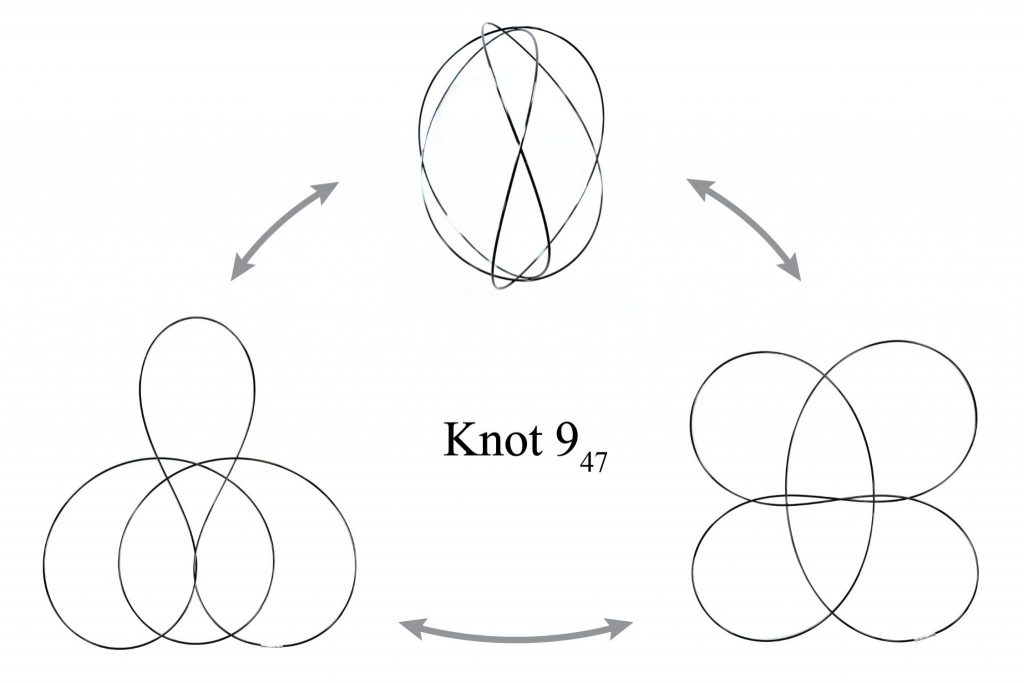
- Elastic knots are physical realizations of closed curves embedded in 3-space. When endowed with the material thickness and bending resistance of a physical wire, these knots settle into equilibrium states that balance the forces induced by elastic deformation and self-contacts of the wire. In general, elastic knots can have many distinct equilibrium states, i.e. they are multistable mechanical systems. We propose a computational pipeline that combines randomized spatial sampling and physics simulation to efficiently find stable equilibrium states of elastic knots. Leveraging results from knot theory, we run our pipeline on thousands of different topological knot types to create an extensive data set of multistable knots. By applying a series of filters to this data, we discover new transformable knots with interesting geometric and physical properties. A further analysis across knot types reveals geometric and topological patterns, yielding constructive principles that generalize beyond the currently tabulated knot types. We show how multistable elastic knots can be used to design novel deployable structures and engaging recreational puzzles. Several physical prototypes at di erent scales highlight these applications and validate our simulation.
A sample of 5’330 equilibrium states of the 85 knots with up to 9 crossings (~70MB)
All the 416’980 equilibrium states of the 2’978 knots with up to 12 crossings we computed (~6GB)
The 2’978 knots with up to 12 crossings as cubic lattice curves (~50MB)
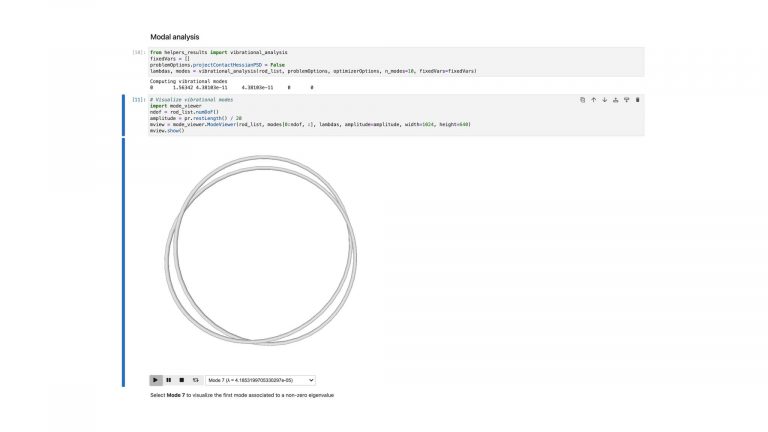
To compute equilibrium states of elastic knots we sample closed curves on the cubic lattice, simulate the relaxation of the corresponding elastic rod with self-contacts, and guarantee topology preservation throughout the process.
By building physical prototypes we validate the correctness of our simulation.
We design novel puzzles in which the user is challenged to deform an elastic knot and make it assume the prescribed equilibrium states.
Some of our knots can jump!
Publications
