Our goal is to improve a joint limits representation that has the following characteristics :
- captures intra- and inter-joint coupling,
- is easy to derive on the basis of live motion recordings,
- allows rapid determinant of the validity of a rotation.
Test-bed joints at the shoulder and upper arm level
 Joints at the upper arm level present both intra- and inter-joint coupling, and are therefore an ideal location for validating our joint limits representation. Intra-joint coupling is present at the gleno-humeral 3 degree-of-freedom (DOF) joint level (or “shoulder joint”) . Inter-coupling is present between the 2 DOF sterno-clavicular joint (or “clavicular” joint) and the shoulder joint, as well as between the latter and the elbow joint. The first coupling is purely due to joint geometry, whereas the second is not only due to anatomical reasons, but also to body part collision. Indeed, flexion of the elbow is limited for certain shoulder joint positions, as the presence of the thorax or head acts as a limiting factor.
Joints at the upper arm level present both intra- and inter-joint coupling, and are therefore an ideal location for validating our joint limits representation. Intra-joint coupling is present at the gleno-humeral 3 degree-of-freedom (DOF) joint level (or “shoulder joint”) . Inter-coupling is present between the 2 DOF sterno-clavicular joint (or “clavicular” joint) and the shoulder joint, as well as between the latter and the elbow joint. The first coupling is purely due to joint geometry, whereas the second is not only due to anatomical reasons, but also to body part collision. Indeed, flexion of the elbow is limited for certain shoulder joint positions, as the presence of the thorax or head acts as a limiting factor.
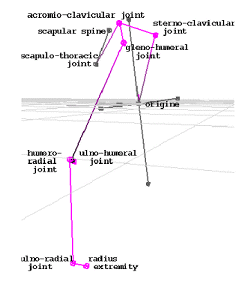
The shoulder joint complex can be graphically represented as per the Figure on the right, as taken from Walter Maurel’s PhD.
New parameterisation of joints
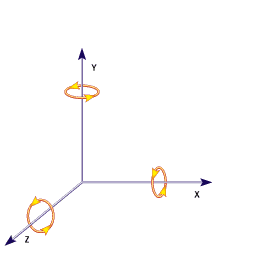 In all inventoried motion capture applications, joint limits have been represented as min/max ranges on Euler angle rotations, which is particularly problem in the case of 3 DOF joints, as:
In all inventoried motion capture applications, joint limits have been represented as min/max ranges on Euler angle rotations, which is particularly problem in the case of 3 DOF joints, as:
- the representation does not reflect realitz, as the rotation of a joint is decomposed into three successive rotations around the x,y,z axes (see Figure hereunder);
- it is mathematically flawed, leading to the Gimbal lock singularity;
- each 3D rotation has several Euler angles representations.
For a comparison of the various rotation representations, see Bobick N., “Rotating Objects Using Quaternions”, Game Developer, July 3, 1998, Vol. 2: Issue 26, that focuses on the quaternion representation.
Biomechanical constraints: automatic determination of joint limits
In order to automatically determine the joint limits, we propose to capture clavicle, shoulder and elbow motions using the Vicon optical motion capture system, where the subject tries to cover the complete space of attainable orientations. An example of such a motion can be seen in this video.
 From the 3D marker positions provided by the Vicon, we can infer the corresponding clavicle, shoulder and elbow rotations by constructing a local referential at each joint in each sequence frame (see Figure below). This idea originates from Prof. A. Hanson’s publications. We now have a path of rotating referentials.
From the 3D marker positions provided by the Vicon, we can infer the corresponding clavicle, shoulder and elbow rotations by constructing a local referential at each joint in each sequence frame (see Figure below). This idea originates from Prof. A. Hanson’s publications. We now have a path of rotating referentials.
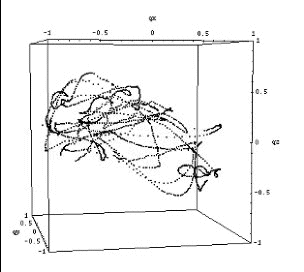
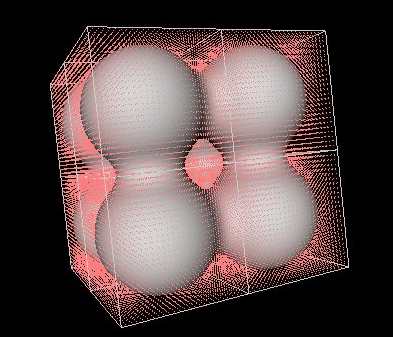
These paths can be expressed in unit quaternion space, this rotation representation overcoming the problems that hamper Euler angles. The unitary condition renders the scalar component redundant, and we can therefore visualise the unit quaternion rotations in 3D, as points within a sphere of radius 1.0 (see Figure bottom right).
For our shoulder motions captured with the Vicon (left image, below), we get a cloud of quaternions viewed in 3D such as the one depicted in the image below (right image, below).
To derive a notion of valid/invalid rotations, we would like to approximate the obtained data points by an envelope. The idea is therefore to wrap an implicit surface around them.
The data for the right clavicula, shoulder and elbow looks as in the Figure hereunder, from left to right. In order to fit this data to an implicit surface, we would in theory first need to extract its surface points. However, given that our data is not homogeneously dense, especially so around the borders, attempting to extract surface points has proven to be a vain enterprise.
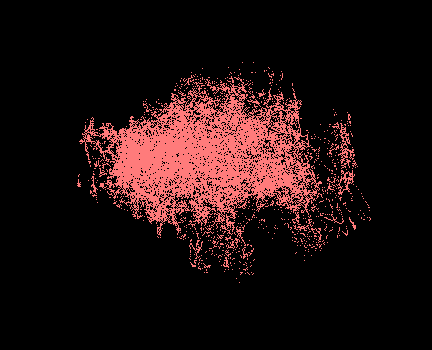

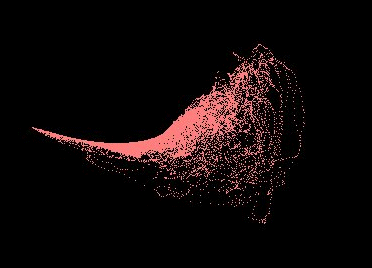
Instead, we approached the problem directly from the volumetric perspective. However, the clavicule and elbow quaternions were first converted to 2D Euler angles, as their surface-like shape would have been more difficult to handle. If it is true that for representing 3 DOF rotations, Euler angles are a bad choice, due to their singularity, this is not the case for 2 DOF rotations. The result of this conversion is shown in the image below, on the left and middle.
We approximate our 3D quaternions and 2D Euler angles by an implicit surface as follows: the data is voxelised with sufficient resolution in order to capture the details of the data shape. In each voxel belonging to the shape, we place a spherical primitive – or metaball – the definition of its field function being adapted from the article of Bittar, Tsingos and Cani’s algorithm. This concept is illustrated in the image below, on the right.
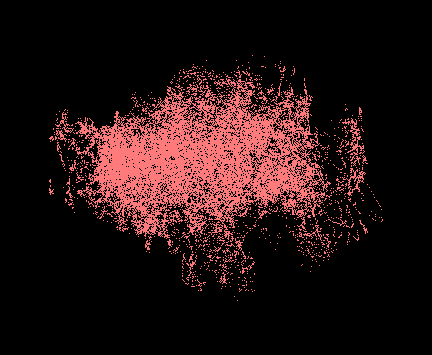
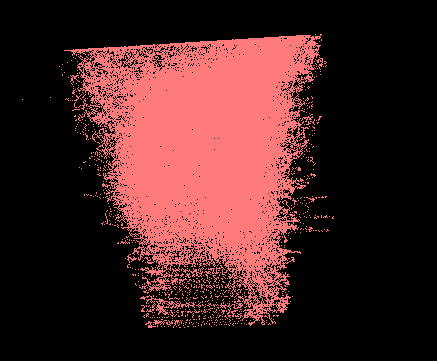
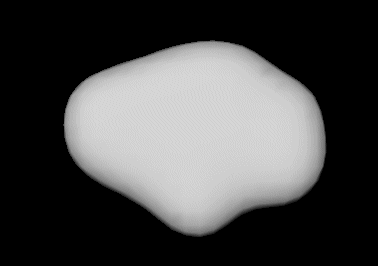
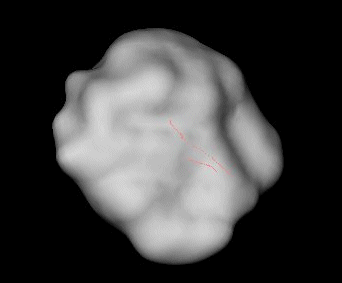
Once the metaballs positioned within each voxel, we just need to extract the iso-contour, thus obtaining a representation of the range of motion boundary, for each joint, as shown in the Figure hereunder, for the clavicle, shoulder and elbow rotations respectively.

We now have joint limits for each joint separately, but still have not captured the coupling that exists between their respective ranges of motion. To achieve this, we will re-use the voxelisation idea, applying a coarser voxelisation to the clavicle and shoulder joint data respectively, for each joint couple. Each voxel so defines a cluster of similar rotations. Having measured clavicle/shoulder and shoulder/elbow rotations simultaneously, the corresponding child joint rotations for each such parent joint cluster are immediately obtained. These data points are approximated in turn by an implicit surface, with the technique presented above. The general idea is laid out in the Figure below :
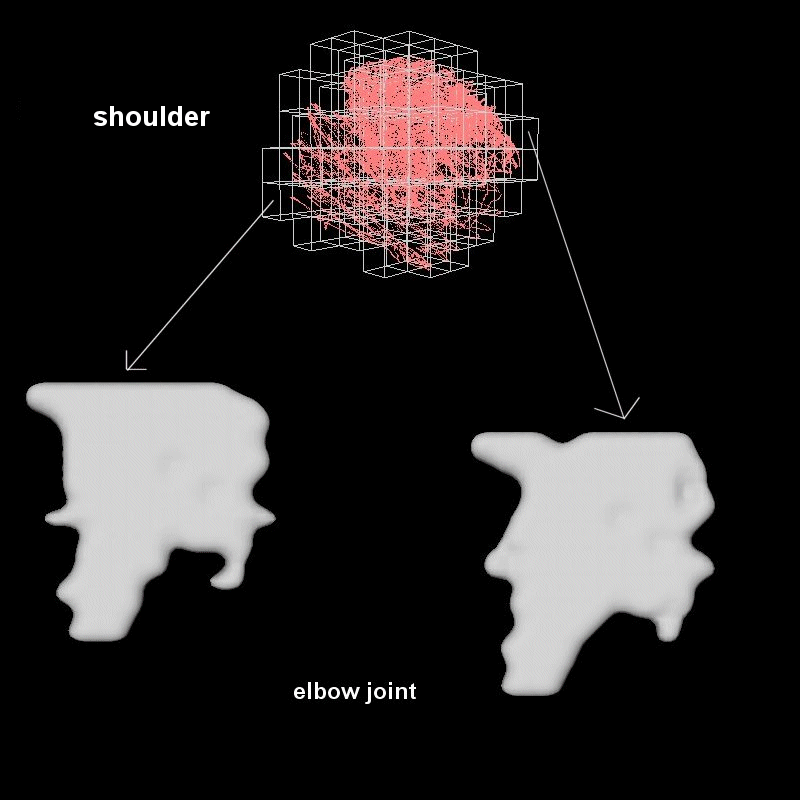
In order to obtain smoother transitions in child joint limits, we insert additional voxels at the parent joint level and obtain the corresponding child joint limits by morphing between the corresponding neighbour surfaces. The surfaces obviously being similar from one cluster to the next, simple linear interpolation between the primitives’ centres and radii is sufficient.
With this hierarachial joint limits set-up, we can enforce range of motion boundaries in character animation as well as in video motion capture.
In animation, the limits are enforced in the following manner. For each rotation set by the animator or defined by a keyframe sequence, it is converted to a unit quaternion and checked with respect to the implicit surface joint limits. If it is an incorrect position, we will clamp it to the closest valid position, by moving along the total gradient towards the surface of the implicit surface, the intersection with this ray being the new valid position, determined by dichotomy.
In video-based motion capture, the joint limits are enforced by damped least-squares with a task-priority scheme. When optimising the joint rotations of the model so that it matches the data, we define tasks of different priorities. Joint limits need to be enforced at all times, so they become the task of higher priority. In the case of coupled joints, the parent joint has the highest priority. The task of lowest priority then becomes the minimisation of the distance between the model and the data. This task-priority strategy can be read up in the publication of Paolo Baerlocher.
Character animation
An example of joint limits enforcement is shown below, and some videos can be viewed here :
- Flexion motion: without limits front/profile, same motion with limits front/profile)
- Abduction motion: without limits front/profile, same motion with limits front/profile)
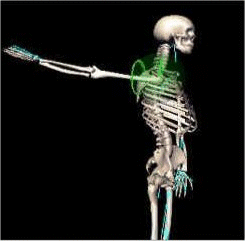
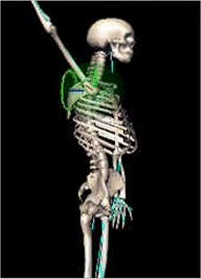
Applying the joint limits to random motion (on the right), where the original keyframe sequence was voluntarily modified with incorrect rotations (on the left) :
Video-based motion capture
We show several examples of posture recovery on the basis of stereo data extracted from video sequences. In the top row, in each case, we show the motion recovered without applying joint limits. The first video shows a projection of the recovered skeleton postures with the original video sequence. The second video shows the metaball-fleshed out body model superposed onto the stereo data, and the third video, just the skeleton once again with the stereo data. Finally, the fourth video shows the recovered motion applied to an anatomical skeleton model, so that the errors become more obvious to the eye. The recovered motion this time using constrained posture recovery is shown in the second row, for each case.
Clavicle and shoulder motion
Shoulder and elbow motion
Publications
Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.
Automatic Determination of Shoulder Joint Limits using Experimentally Determined Quaternion Field Boundaries
International Journal of Robotics Research. 2003. Vol. 22, num. 6, p. 419-436. DOI : 10.1177/0278364903022006005.Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.