Variant selection in red gold alloys during phase transformation under stress

Context of the project

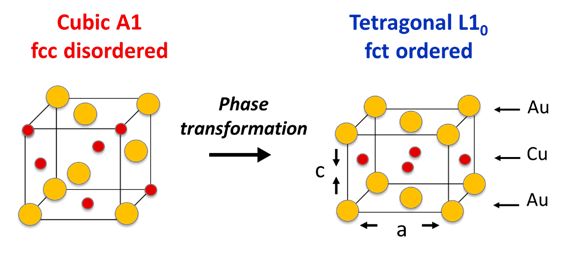
Red gold alloys are of high interest for the luxury industry for their attracting color and for their good mechanical properties. For specific compositions, red gold alloys undergo an order-disorder phase transformation around 400°C, which leads to an ordering of the atoms as well as to a tetragonal distortion from the f.c.c. to a f.c.t. lattice as shown in fig.1. The transformation implies a local diffusion of the atoms and is, thus, diffusive. However, the transformation also displays several features of a displacive transformation like surface relief, specific orientation relationship and shape memory effect. Yet, the displacive aspect of the transformation remains controversial.

The aforementioned shape memory effect must involve variant selection during the displacive transformation occurring under stress. This research project funded by an Innosuisse project aims at analyzing the variant selection in order to understanding the macroscopic behavior of red gold alloys and in particular the shape memory effect. In this work, we use an unconventional approach as we consider the displacive aspect of this transformation.

Latices before (cubic) and after phase transformation (tetragonal)
Fig.1. Schematic of the phase transformation

EBSD analysis

The transformation results in a complex microstructure formed by the arrangement of nano-scale ordered tetragonal domains. Therefore, it has mainly been studied by transmission electron microscopy (TEM) in the literature. In this project and for the first time, the variants could be analyzed by Electron Backscattered Diffraction (EBSD). The use of EBSD enables to make a statistical analysis of the variants among numerous grains on large areas.

A reference stress free sample fully transformed in the f.c.t. phase is shown in fig.2. The three colors, which are visible within the central parent f.c.c. grain on the EBSD map, represent three crystallographic orientations. Yet, our extensive study of the habit planes revealed that there were in fact 12 variants with very close orientations, which can be approximated in three groups of close orientations.

SEM image and EBSD map of a reference sample
Fig.2. Scanning electron microscopy image with secondary electrons (SE) and EBSD map of the tetragonal variants in a stress free reference sample, and schematic of the tetragonal variants

First results

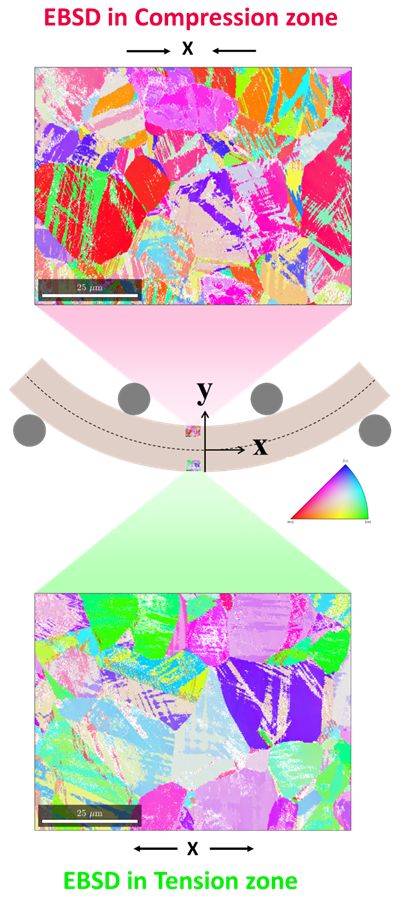
Four-point bent samples are heat treated to enable the phase transformation under stress in order to study the variant selection by EBSD. Several maps are acquired on both sides of the sample as shown in fig.3 in order to study a large number of grains. A first glance at the maps reveal that the crystallographic orientations on both sides are different. The inverse pole figure (IPF) colors of the maps give qualitative information on the variant selection.

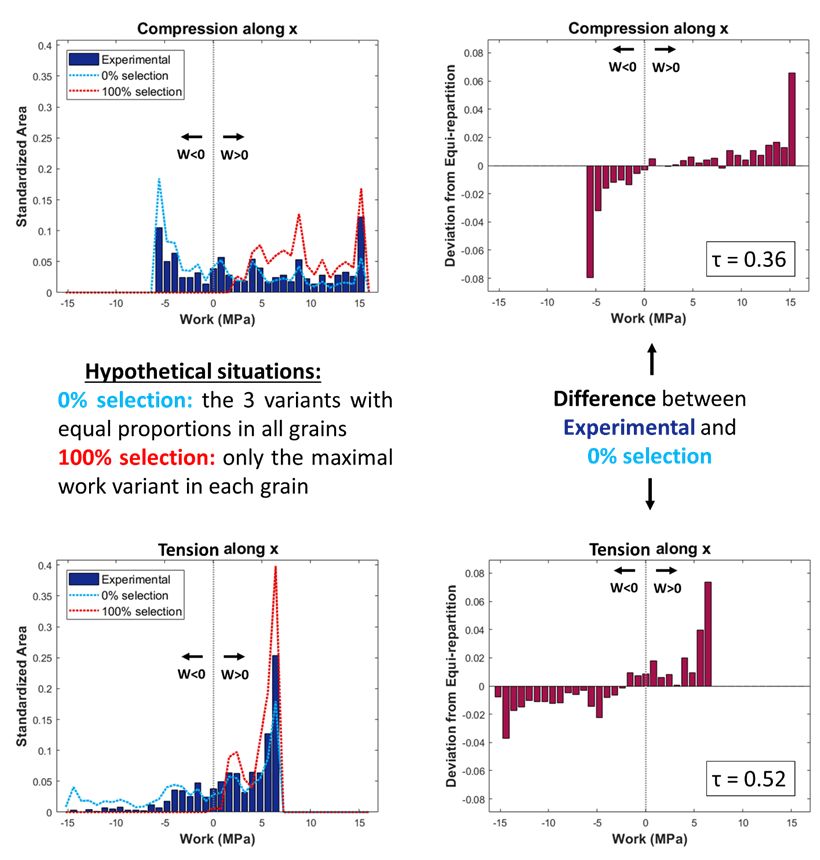
Our in-house Matlab code enables to quantify the variant selection using the maximal work criterion, which states that high work variants are preferentially formed. It computes the mechanical work of variant formation from the distortion matrix, which is calculated from the crystallographic orientation of the variant of the EBSD data. Histograms of work repartition of the variants in numerous grains are compared to the simulated hypothetical case of 0%-selection. As expected, variants with higher work are more numerous than the 0%-selection case as depicted in fig.4. The quantification of the variant selection is possible by the comparison with the calculated 0%-selection and the 100%-selection. The degree of selection τ is 0 of there is no selection and 1 if the variant selection is maximal.

EBSD map of areas under compression and tension
Fig.3. EBSD maps in compression and tension zones of the sample transformed under 4 point bending
Graphs of measured and simulated values
Fig.4. Experimental work distribution histogram compared with the simulated extremal cases

Reference:

Larcher, M. N. D., Cayron, C., Blatter, A., Soulignac, R. & Loge, R. E. (2019). J. Appl. Cryst. 52, 1202-1213.