Contexte du projet
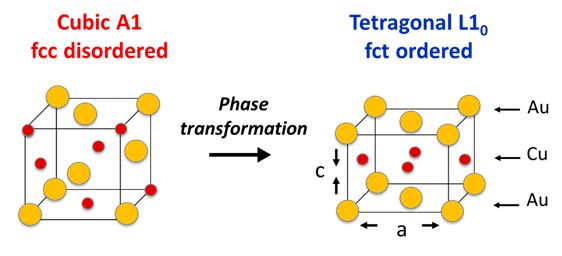
Les alliages d’or rouge sont d’un grand intérêt pour l’industrie du luxe pour leur couleur attirante et pour leurs bonnes propriétés mécaniques. Pour des compositions spécifiques, les alliages d’or rouge subissent une transformation de phase d’ordre-désordre autour de 400°C, ce qui conduit à une mise en ordre des atomes ainsi qu’à une distorsion tétragonale de la maille c.f.c. (cubique face centrée) en une maille t.f.c. (tétragonale face centrée) comme le montre la fig.1. La transformation implique une diffusion locale des atomes et est donc diffusive. Cependant, la transformation affiche également plusieurs caractéristiques d’une transformation displacive comme le relief de surface, des relations d’orientation spécifiques et un effet mémoire de forme. Pourtant, l’aspect displacif de la transformation reste controversé.
L’effet mémoire de forme susmentionné doit impliquer une sélection de variants pendant la transformation displacive se produisant sous contrainte. Ce projet de recherche financé par un projet Innosuisse vise à analyser la sélection des variants afin de comprendre le comportement macroscopique des alliages d’or rouge et en particulier l’effet mémoire de forme. Dans ce travail, nous utilisons une approche non conventionnelle en considérant l’aspect displacif de cette transformation.
Analyse EBSD
La transformation se traduit par une microstructure complexe formée par l’agencement de domaines tétragonaux ordonnés à l’échelle nanométrique. Par conséquent, il a été principalement étudié par microscopie électronique à transmission (MET) dans la littérature. Dans ce projet et pour la première fois, les variants ont pu être analysés avec un microscope électronique à balayage (MEB) par diffraction d’électrons rétrodiffusés (EBSD). L’utilisation d’EBSD permet de faire une analyse statistique des variants parmi de nombreux grains sur de grandes surfaces.
Un échantillon de référence sans contraintes, entièrement transformé en phase t.f.c. est montré dans la fig.2. Les trois couleurs, qui sont visibles dans le grain parent central c.f.c. sur la carte EBSD, représentent trois orientations cristallographiques. Pourtant, notre étude approfondie des plans d’habitat a révélé qu’il y avait en fait 12 variants avec des orientations très proches, qui peuvent être approximés par trois groupes d’orientations proches.

Premiers résultats
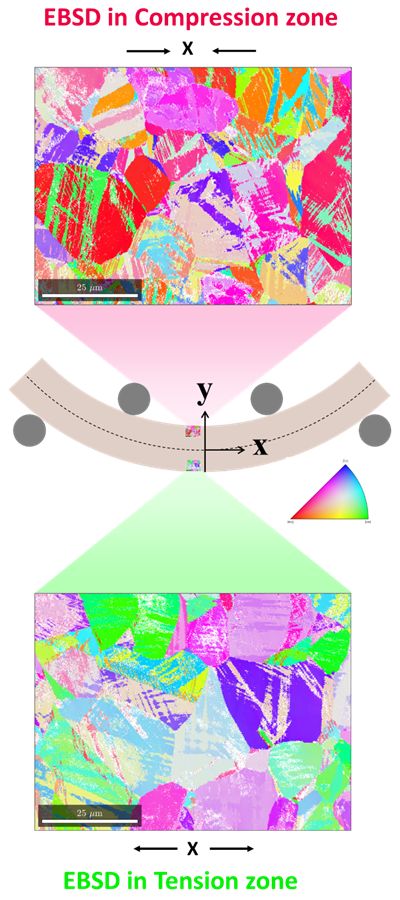
Les échantillons déformés en flexion quatre points sont traités thermiquement pour permettre la transformation de phase sous contrainte afin d’étudier la sélection des variants par EBSD. Plusieurs cartes sont acquises des deux côtés de l’échantillon comme le montre la fig.3 afin d’étudier un grand nombre de grains. Un premier coup d’œil sur les cartes révèle que les orientations cristallographiques des deux côtés sont différentes. Les couleurs de figures de pôles inverses (IPF ou inverse pole figure) sur les cartes donnent des informations qualitatives sur la sélection des variants.
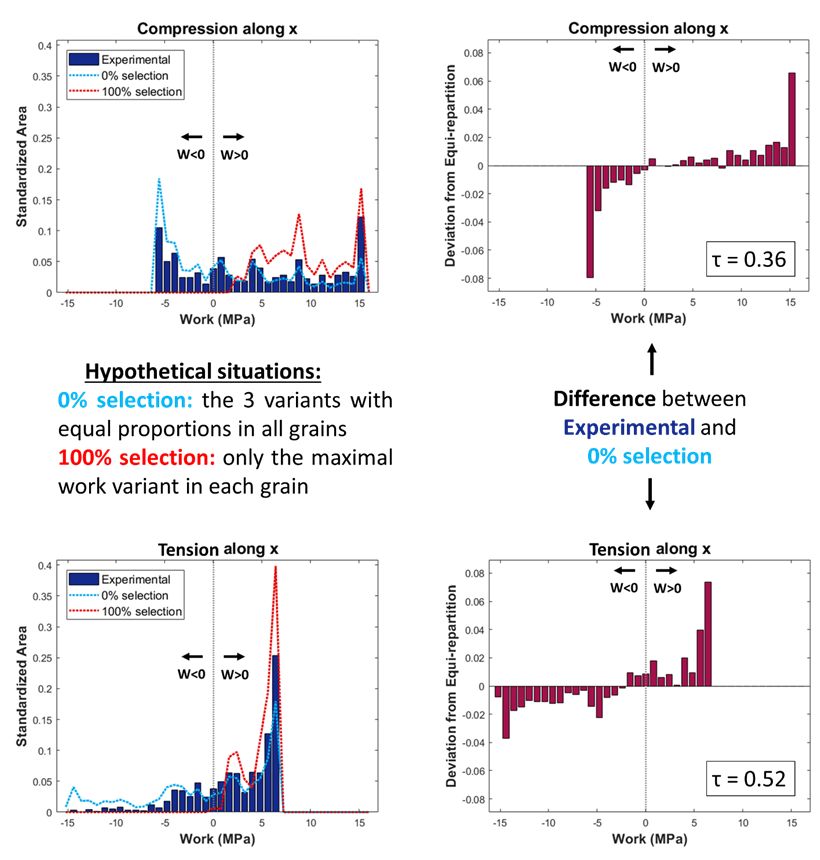
Notre code Matlab développé en interne permet de quantifier la sélection des variants en utilisant le critère de travail maximal, qui stipule que les variants à travail élevé sont formés préférentiellement. Il calcule le travail mécanique de formation de variants à partir de la matrice de distorsion, qui est calculée à partir de l’orientation cristallographique du variant tirée des données EBSD. Les histogrammes de répartition du travail des variants dans de nombreux grains sont comparés au cas hypothétique simulé avec 0% de sélection. Comme prévu, les variants avec un travail plus élevé sont plus nombreux que le cas 0% de sélection comme illustré dans la fig.4. La quantification de la sélection des variants est possible par la comparaison entre les cas calculés avec 0% de sélection et 100% de sélection. Le degré de sélection τ est 0 s’il n’y a pas de sélection et 1 si la sélection des variants est maximale.
Références
Larcher, M. N. D., Cayron, C., Blatter, A., Soulignac, R. & Loge, R. E. (2019). J. Appl. Cryst. 52, 1202-1213.