Understanding the mechanics of thin elastic rods under geometrically nonlinear configurations is a major thrust of our research. There is a recognized importance of filament-like structures across a wide range of length scales: from the coiling of nanotubes to transoceanic cables and pipelines. The postbuckling regime of slender elastic rods is typically underpinned by a complex energy landscape, hystheresis, and multistability. As such, closed analytical solutions are often out of reach and well-established computational techniques (e.g., the finite element method) can be limited in these scenarios. We seek to circumnavigate these challenges by gaining physical insight from precision model experiments with elastic rods, coupled with scaling analyses and numerical tools, the discrete elastic rod (DER) method, that we have ported from the Computer Graphics community in collaboration with Eitan Grinspun (Columbia University).
Topics that we have investigated on the mechanics of thin rods include: mechanics of elastic knots, coiling patterns of a thin rod deployed onto a rigid substrate, buckling of coiled tubing injected into horizontal wellbores, deformation and buckling of helical rods rotating in a viscous fluid and the mechanics of curly hair. A more detailed account of these examples and other problems is provided below.
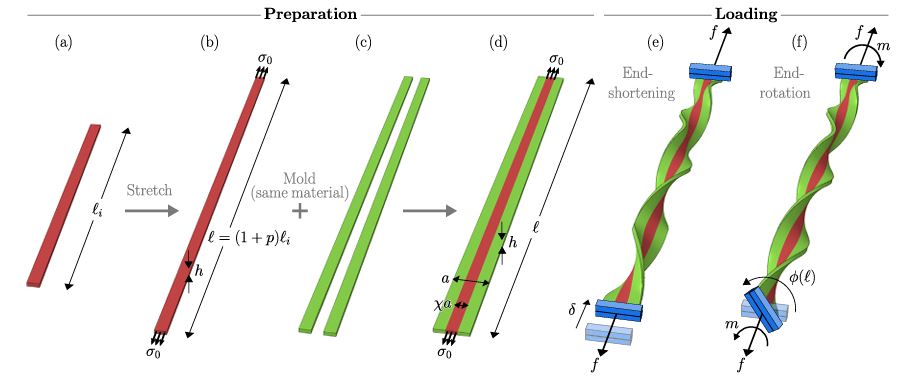
| Twisting instabilities in elastic ribbons with inhomogeneous pre-stress: A macroscopic analog of thermodynamic phase transition
with: Michael Gomeza and Basile Audoly |
 |
|
We study elastic ribbons subject to large, tensile pre-stress confined to a central region within the cross-section. These ribbons can buckle spontaneously to form helical shapes, featuring regions of alternating chirality (phases) that are separated by so-called perversions (phase boundaries). This instability cannot be described by classical rod theory, which incorporates pre-stress through effective natural curvature and twist; these are both zero due to the mirror symmetry of the pre-stress. Using dimension reduction, we derive a one-dimensional (1D) ‘rod-like’ model from a plate theory, which accounts for inhomogeneous pre-stress as well as finite rotations. The 1D model successfully captures the qualitative features of torsional buckling under a prescribed end-to-end displacement and rotation, including the co-existence of buckled phases possessing opposite twist. It is in good quantitative agreement with the results of numerical (finite-element) simulations and model experiments on elastomeric samples. Our model system provides a macroscopic analog of phase separation and pressure–volume–temperature state diagrams, as described by the classical thermodynamic theory of phase transitions. Publications: |
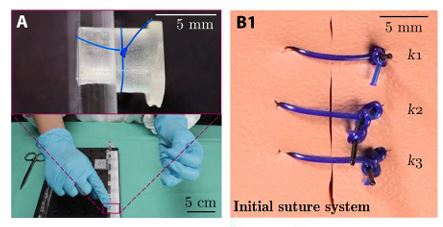
| The strength of surgical knots involves a critical interplay between friction and elastoplasticity
with: Paul Johanns,Changyeob Baek,Paul Grandgeorge, Samia Guerid, and Shawn A. Chester |
 |
|
Knots are the weakest link in surgical sutures, serving as mechanical ligatures between filaments. Exceeding their safe operational limits can cause fatal complications. The empirical nature of present guidelines calls for a predictive understanding of the mechanisms underlying knot strength. We identify the primary ingredients dictating the mechanics of surgical sliding knots, highlighting the previously overlooked but critical effect of plasticity and its interplay with friction. The characterization of surgeon-tied knots reveals the relevant ranges of tightness and geometric features. Using model experiments coupled with finite element simulations, we uncover a robust master curve for the target knot strength versus the tying pre-tension, number of throws, and frictional properties. These findings could find applications in the training of surgeons and robotic-assisted surgical devices. Publications: |
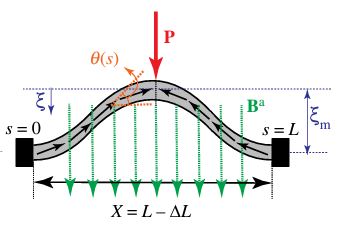
| Snap buckling of bistable beams under combined mechanical and magnetic loading
with: Arefeh Abbasi, Tomohiko G. Sano, and Dong Yan |
 |
|
We investigate the mechanics of bistable, hard-magnetic, elastic beams through a combination of experiments, finite-element modeling (FEM), and a reduced-order theory. The beam, constructed from a hard magnetorheological elastomer, consists of two segments with antiparallel magnetization along the centerline and is induced into a bistable curved configuration by imposing end-to-end shortening. Reversible snapping is achievable between these two stable states. Firstly, we experimentally characterize the critical field strength for the onset of snapping at different levels of end-to-end shortening. Secondly, we conduct three-dimensional FEM simulations using the Riks method to analyze high-order deformation modes during snapping. Thirdly, we develop a reduced-order centerline-based beam theory to rationalize the observed magneto-elastic response. The theory and simulations are validated against experiments, demonstrating excellent quantitative agreement. Finally, we explore the case of combined magnetic loading and poking force, examining how the applied field influences bistability and quantifying the maximum load-bearing capacity. Our work furnishes a set of predictive tools for the rational design of one-dimensional, bistable, magneto-elastic structural elements. Publications: |
| Indentation and stability of woven domes
with: Samuel Poincloux, Célestin Vallat, Tian Chen, and Tomohiko G. Sano |
 |
|
Discrete domes are doubly curved structures comprising a network of beam-like elements. We study the mechanics of discrete domes made of ribbons woven in a pentagonal triaxial pattern. Experiments and finite element simulations are performed to characterize the mechanical response of each woven dome under indentation. The observed nonlinear response features force maxima, snap-through inversion, and non-monotonic evolution, leading to additional stable configurations. The dome’s rest shape can be tuned continuously by designing the in-plane curvature of the ribbons and is then perturbed by adjustable clamped boundary conditions at their extremities. These control parameters are leveraged to smoothly and selectively modify the nonlinear features of the mechanical response, including multi-stability. Finally, we suggest a simplified model based on an elastica approximation to predict the stability of the inverted state successfully. The strong geometrical constraints imposed by the weaving pattern and the ribbons enable us to rationalize and tune the indentation response of these intriguing discrete structures. Publications: |
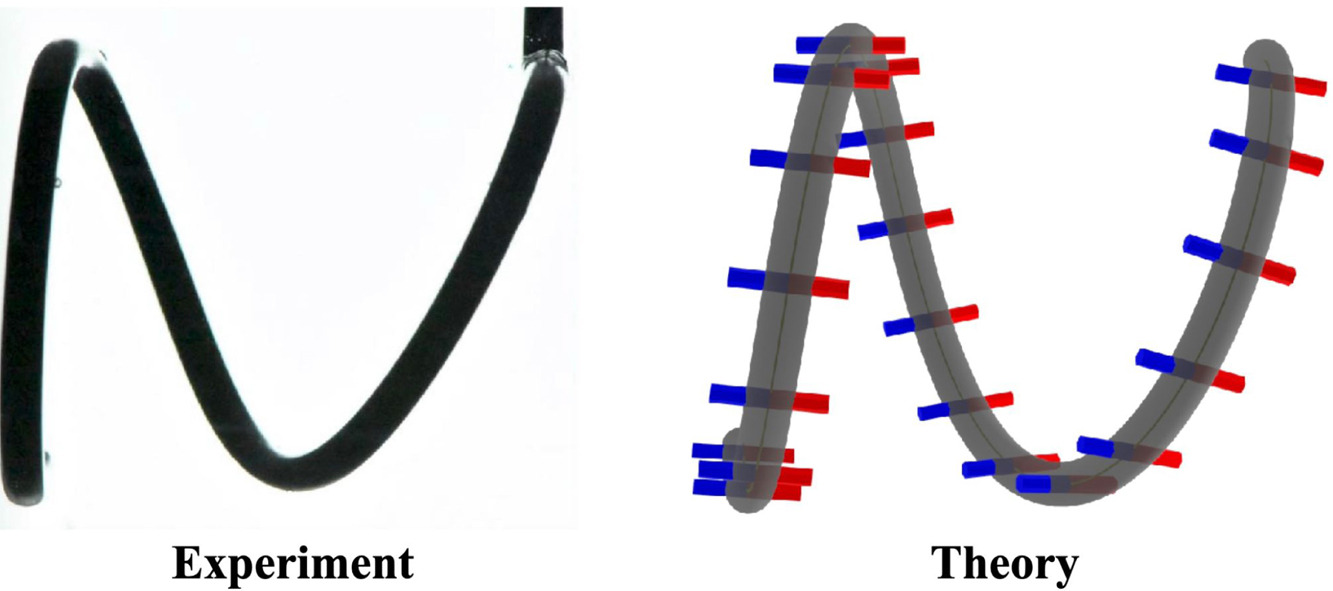
| A Kirchhoff-like theory for hard magnetic rods under geometrically nonlinear deformation in three dimensions
with: Tomohiko G. Sano and Matteo Pezzulla |
 |
|
Magneto-rheological elastomers (MREs) are functional materials that can be actuated by applying an external magnetic field. MREs comprise a composite of hard magnetic particles dispersed into a nonmagnetic elastomeric (soft) matrix. Hard MREs have been receiving particular attention because the programmed magnetization remains unchanged upon actuation. Motivated by a new realm of applications, there have been significant theoretical developments in the continuum (three-dimensional) description of hard MREs. In this paper, we derive an effective theory for MRE rods (slender, mono-dimensional structures) under geometrically nonlinear deformation in three dimensions. Our theory is based on reducing the three-dimensional magneto-elastic energy functional for the hard MREs into an one-dimensional Kirchhoff-like description (centerline-based). Restricting the theory to two dimensions, we reproduce previous works on planar deformations. For further validation in the general case of three-dimensional deformation, we perform precision experiments with both naturally straight and curved rods under either constant or constant-gradient magnetic fields. Our theoretical predictions are in excellent agreement with both discrete simulations and precision-model experiments. Finally, we discuss some limitations of our framework, as highlighted by the experiments, where long-range dipole–dipole interactions, which are neglected in the theory, can play a role. Publications: |
| A comprehensive framework for hard-magnetic beams: Reduced-order theory, 3D simulations, and experiments
with: Dong Yan and Arefeh Abbasi |
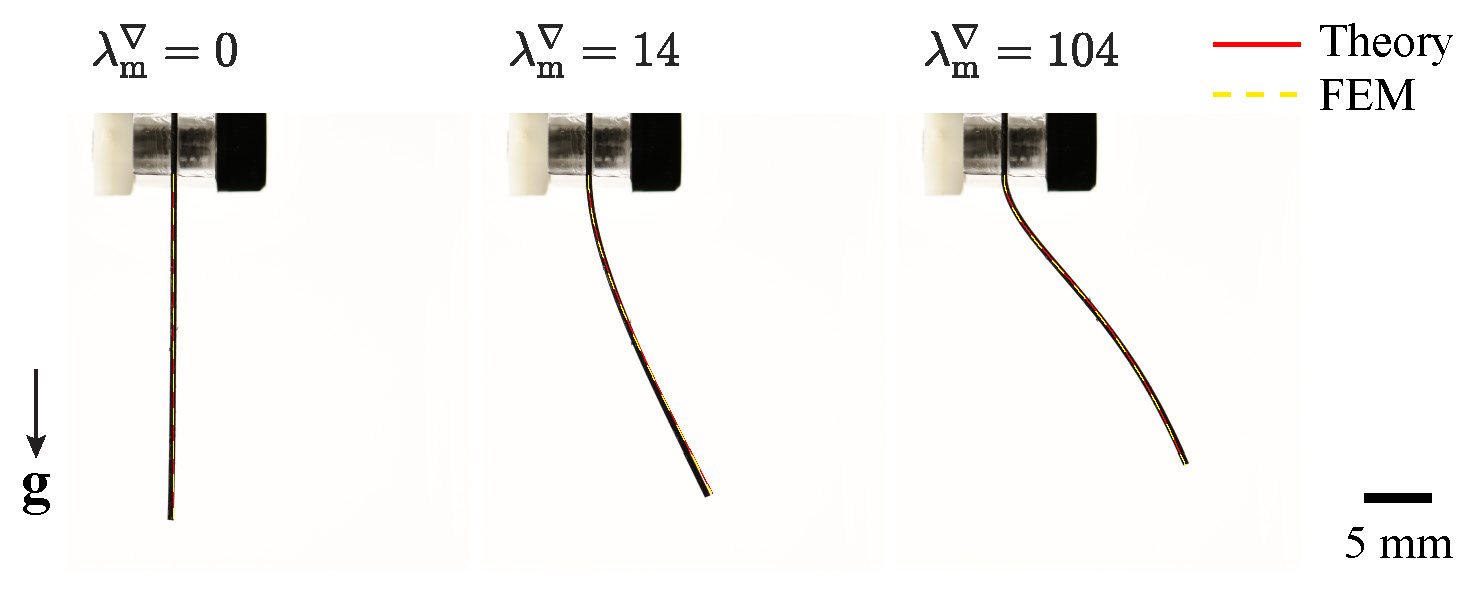 |
|
Thin beams made of magnetorheological elastomers embedded with hard-magnetic particles (hard-MREs) are capable of large deflections under an applied magnetic field. We propose a comprehensive framework, comprising a beam model and 3D finite element modeling (FEM), to describe the behavior of hard-MRE beams under both uniform and constant gradient magnetic fields. First, based on the Helmholtz free energy of bulk (3D) hard-MREs, we perform dimensional reduction to derive a 1D description and obtain the equilibrium equation of the beam through variational methods. In parallel, we extend the existing 3D continuum theory for hard-MREs to the general case of non-uniform fields by incorporating the magnetic body force induced by the field gradient and implementing it in FEM. Then, we validate the beam model and FEM using experiments on a cantilever beam in either a uniform or a constant gradient field, and identify the dimensionless parameters governing the magneto-elastic coupling. Further, a set of comparative numerical studies for different field configurations and magnetization profiles yields additional insight into the beam response. Our study builds on previous work on hard-MRE beams, while providing a more complete framework, both in terms of the methodologies used and the broader range of configurations considered, serving as a valuable predictive toolbox for the rational design of beam-like hard-magnetic structures. Publications: |
| Smooth triaxial weaving with naturally curved ribbons
with: Changyeob Baek, Alison G. Martin, Samuel Poincloux, and Tian Chen |
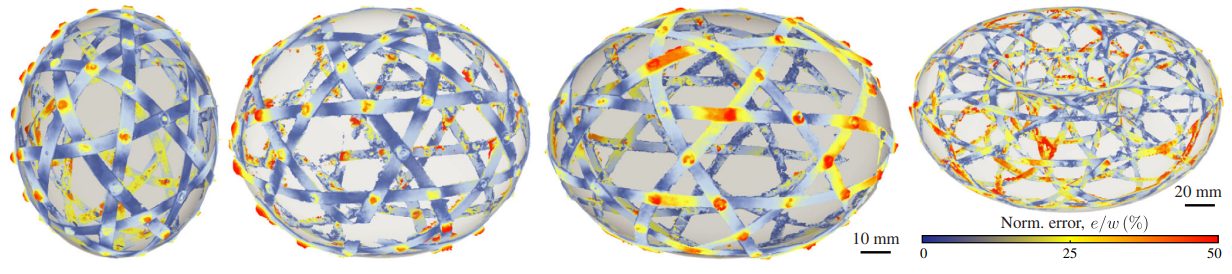 |
|
Triaxial weaving is a handicraft technique that has long been used to create curved structures using initially straight and flat ribbons. Weavers typically introduce discrete topological defects to produce nonzero Gaussian curvature, albeit with faceted surfaces. We demonstrate that, by tuning the in-plane curvature of the ribbons, the integrated Gaussian curvature of the weave can be varied continuously, which is not feasible using traditional techniques. Further, we reveal that the shape of the physical unit cells is dictated solely by the in-plane geometry of the ribbons, not elasticity. Finally, we leverage the geometry-driven nature of triaxial weaving to design a set of ribbon profiles to weave smooth spherical, ellipsoidal, and toroidal structures. Publications: |
| Exploring the inner workings of the clove hitch knot
with: Tomohiko G. Sano, Paul Johanns, Paul Grandgeorge, and Changyeob Baek |
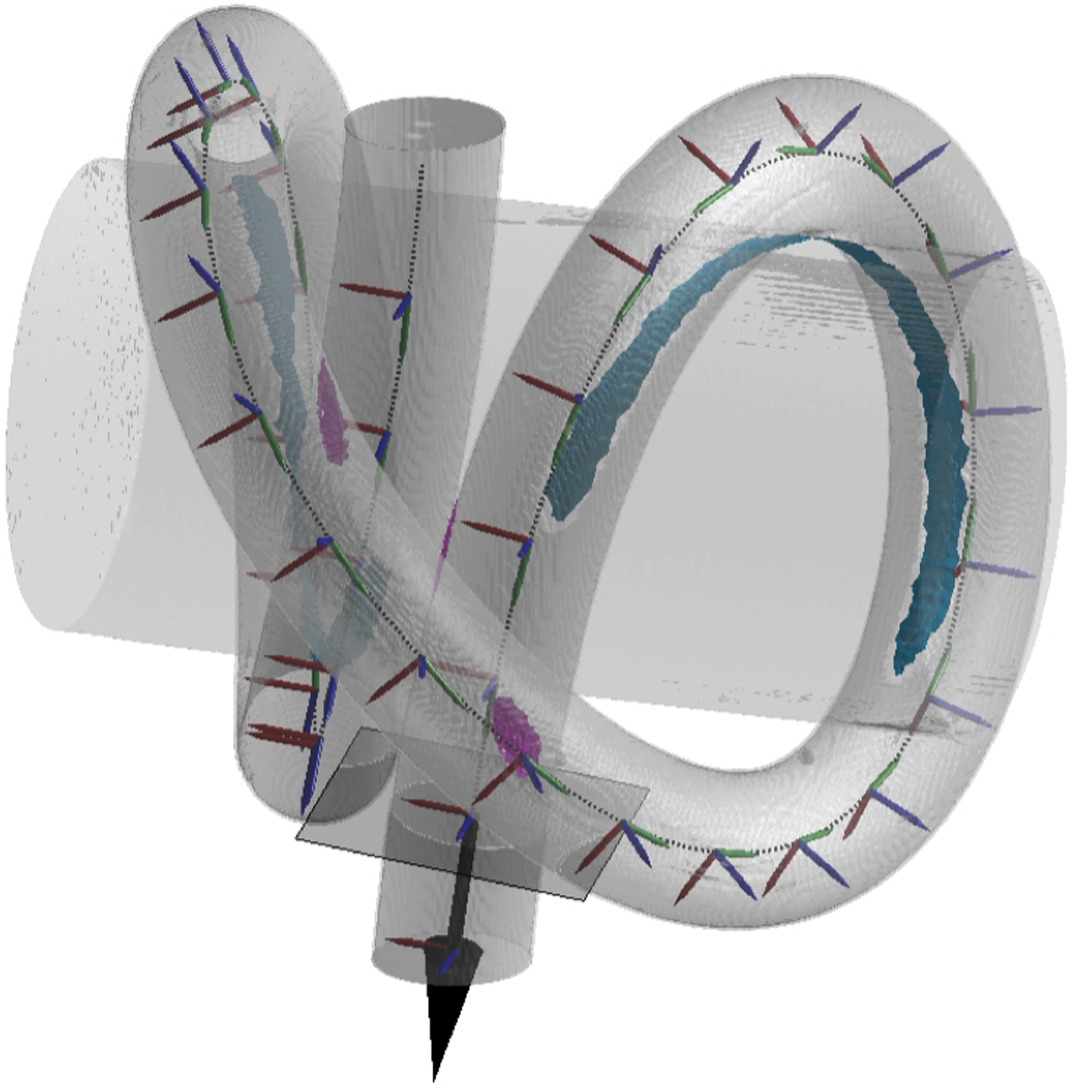 |
|
We perform a combined experimental and computational investigation of the clove hitch knot. We develop a physical model for the clove hitch by tying an elastic rod onto a rigid cylinder. In the experiments, we characterize the mechanical performance, geometry, and stability conditions of the knot. X-ray tomography allows us to characterize the 3D geometry of the rod centerline. These results also serve to validate our finite element modeling (FEM), which we use to quantify the tension profile, not accessible experimentally, along the knotted rod. We find that the clove hitch comprises alternating segments with two types of contact regions: one where the rod is in single frictional contact with the cylinder, and another with rod self-contact (where a rod segment pinches another against the cylinder). In the first region, the internal tension decays exponentially (akin to the capstan configuration), whereas, in the second, the pinch (nip) regions lead to discontinuous tension drops. We analyze these nip regions with an even simpler model system where an elastic rod is pinched between two rigid cylinders. Despite the complex contact geometry of this pinching experiment, we find that the frictional behavior of our model systems still obeys the classic Amontons-Coulomb law. Ultimately, we can regard the clove hitch knot, if tied correctly, as a functional structure enabling to drop high tension at one extremity of a filament secured onto a rigid post, all the way to zero at the other extremity. Publications: |
| An elastic rod in frictional contact with a rigid cylinder
with: Paul Grandgeorge and Tomohiko G. Sano |
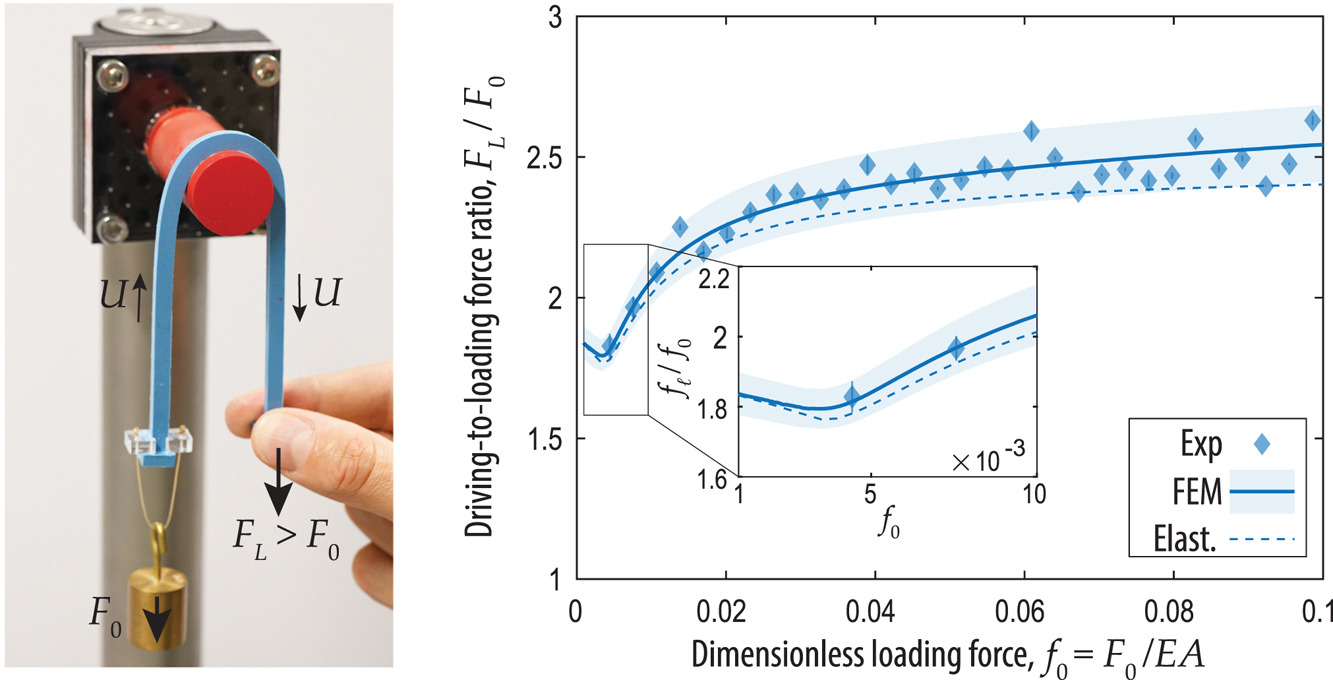 |
|
We investigate the load transmission along an elastic rod of finite cross-section in contact with a rigid cylinder, as system often referred to as the generalized capstan problem. In the presence of friction, the idealized classic capstan equation predicts that the tension along a perfectly thin and flexible filament increases exponentially along the contact region. In practical applications, however, the validity of the idealized capstan equation is compromised due to the interplay between finite rod thickness, bending stiffness, and the forces applied at the rod extremities. Here, we combine precision model experiments, finite element simulations, and theoretical modeling to investigate the contact mechanics and the force transmission along an elastic rod in frictional contact with a rigid cylinder. We study two cases when the rod is either static or sliding. First, we focus on the static case, in the absence of friction, by considering equal loads at both extremities of the rod. We show that as the loading force is increased, the nature of contact transitions from a localized region to an extended band at the surface of the cylinder. The latter is characterized by double-peaked contact force distribution. In the sliding case, friction is activated by inducing a relative motion between the rod and the cylinder. We applied a fixed loading force at one rod extremity while pulling the other extremity at a constant velocity. The driving force is monitored during sliding. For increasing loading forces, we find that the force ratio is non-monotonic and displays a local minimum, in contradiction with the constant ideal capstan prediction. This minimum force ratio coincides with the transition from a single contact point to an extended contact region. A theoretical analysis based on Euler’s elastica serves to rationalize the results from the physical and numerical experiments. In addition to predicting the nature of the contact region (single point versus extended line), our model provides quantitative predictions for the wrapping angle and the driving-to-loading force ratio. Finally, we leverage our mechanics-based framework to predictively understand the force ratio at the ends of two commercially available engineering belts (spring-steel and polyurethane) in sliding contact with a steel cylinder. Publications: |
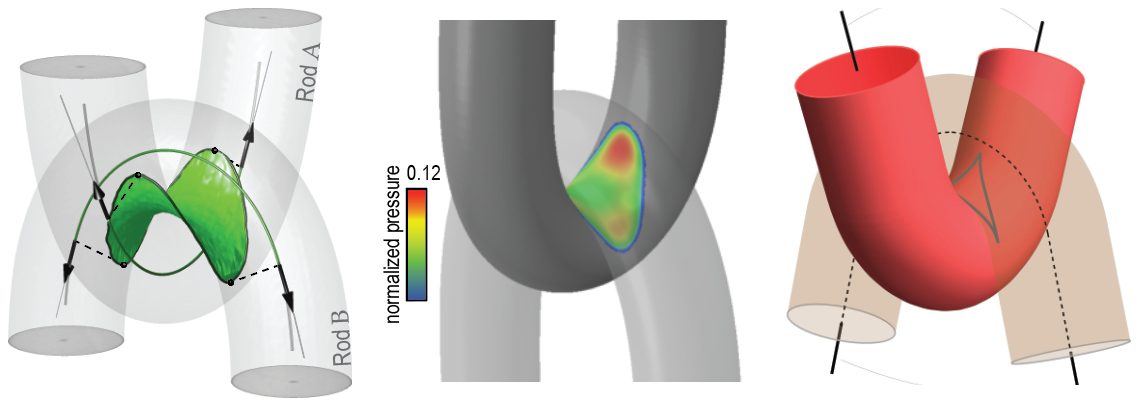
| Mechanics of two filaments in tight orthogonal contact
with: Paul Grandgeorge, Changyeob Baek, Harmeet Singh, Paul Johanns, Tomohiko G. Sano, Alastair Flynn, and John H. Maddocks |
 |
|
Networks of flexible filaments often involve regions of tight contact. Predictively understanding the equilibrium configurations of these systems is challenging due to intricate couplings between topology, geometry, large nonlinear deformations, and friction. Here, we perform an in-depth study of a simple, yet canonical, problem that captures the essence of contact between filaments. In the orthogonal clasp, two filaments are brought into contact, with each centerline lying in one of a pair of orthogonal planes. Our data from X-ray tomography (μCT) and mechanical testing experiments are in excellent agreement with finite element method (FEM) simulations. Despite the apparent simplicity of the physical system, the data exhibit strikingly unintuitive behavior, even when the contact is frictionless. Specifically, we observe a curvilinear diamond-shaped ridge in the contact-pressure field between the two filaments, sometimes with an inner gap. When a relative displacement is imposed between the filaments, friction is activated, and a highly asymmetric pressure field develops. These findings contrast to the classic capstan analysis of a single filament wrapped around a rigid body. Both the μCT and FEM data indicate that the cross-sections of the filaments can deform significantly. Nonetheless, an idealized geometrical theory assuming undeformable tube cross-sections and neglecting elasticity rationalizes our observations qualitatively and highlights the central role of the small, but nonzero, tube radius of the filaments. We believe that our orthogonal clasp analysis provides a building block for future modeling efforts in frictional contact mechanics of more complex filamentary structures. Publications: |
| The shapes of physical trefoil knots
with: Paul Johanns, Paul Grandgeorge, Changyeob Baek, Tomohiko G. Sano, and John H. Maddocks |
 |
|
We perform a compare-and-contrast investigation between the equilibrium shapes of physical and ideal trefoil knots, both in closed and open configurations. Ideal knots are purely geometric abstractions for the tightest configuration tied in a perfectly flexible, self-avoiding tube with an inextensible centerline and undeformable cross-sections. Here, we construct physical realizations of tight trefoil knots tied in an elastomeric rod, and use X-ray tomography and 3D finite element simulation for detailed characterization. Specifically, we evaluate the role of elasticity in dictating the physical knot’s overall shape, self-contact regions, curvature profile, and cross-section deformation. We compare the shape of our elastic knots to prior computations of the corresponding ideal configurations. Our results on tight physical knots exhibit many similarities to their purely geometric counterparts, but also some striking dissimilarities that we examine in detail. These observations raise the hypothesis that regions of localized elastic deformation, not captured by the geometric models, could act as precursors for the weak spots that compromise the strength of knotted filaments. Publications: |
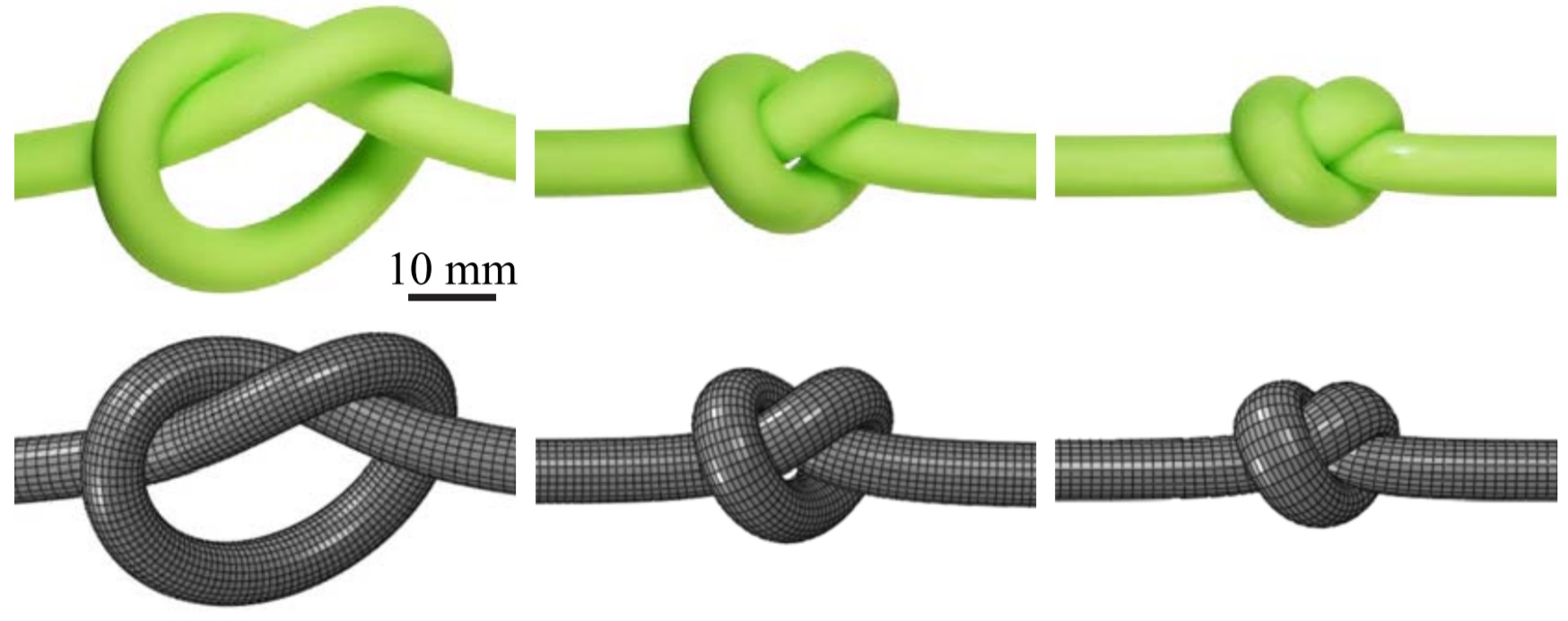
| Finite element modeling of tight elastic knots
with: Changyeob Baek, Paul Johanns, Tomohiko G. Sano, and Paul Grandgeorge |
 |
|
We present a methodology to simulate the mechanics of knots in elastic rods using geometrically nonlinear, full three-dimensional (3D) finite element analysis. We focus on the mechanical behavior of knots in tight configurations, for which the full 3D deformation must be taken into account. To setup the topology of our knotted structures, we apply a sequence of prescribed displacement steps to the centerline of an initially straight rod that is meshed with 3D solid elements. Self-contact is enforced with a normal penalty force combined with Coulomb friction. As test cases, we investigate both overhand and figure-of-eight knots. Our simulations are validated with precision model experiments, combining rod fabrication and X-ray tomography. Even if the focus is given to the methods, our results reveal that 3D deformation of tight elastic knots is central to their mechanical response. These findings contrast to a previous analysis of loose knots, for which 1D centerline-based rod theories sufficed for a predictive understanding. Our method serves as a robust framework to access complex mechanical behavior of tightly knotted structures that are not readily available through experiments nor existing reduced-order theories. Publications: |
| Compressible and electrically conducting fibers for large-area sensing of pressures
with: Andreas Leber, Alexis Gérald Page, Dong Yan, Yunpeng Qu, Shahrzad Shadman, and Fabien Sorin |
 |
|
Flexible pressure sensors offer a wide application range in health monitoring and human–machine interaction. However, their implementation in functional textiles and wearable electronics is limited because existing devices are usually small, 0D elements, and pressure localization is only achieved through arrays of numerous sensors. Fiber‐based solutions are easier to integrate and electrically address, yet still suffer from limited performance and functionality. An asymmetric cross‐sectional design of compressible multimaterial fibers is demonstrated for the detection, quantification, and localization of kPa‐scale pressures over m2‐size surfaces. The scalable thermal drawing technique is employed to coprocess polymer composite electrodes within a soft thermoplastic elastomer support into long fibers with customizable architectures. Thanks to advanced mechanical analysis, the fiber microstructure can be tailored to respond in a predictable and reversible fashion to different pressure ranges and locations. The functionalization of large, flexible surfaces with the 1D sensors is demonstrated by measuring pressures on a gymnastic mat for the monitoring of body position, posture, and motion. Publications: |
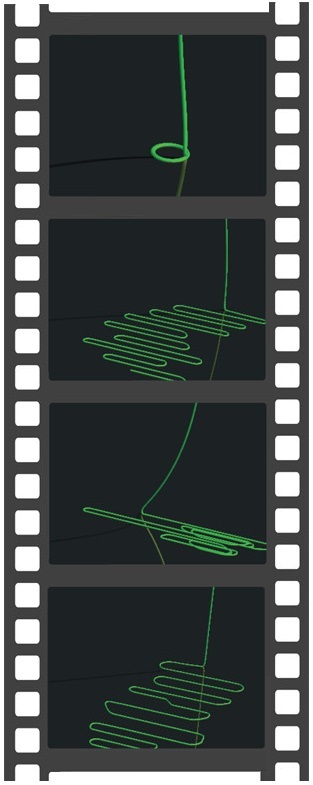
| Patterns of carbon nanotubes by flow-directed deposition on substrates with architectured topographies
with: M. K. Jawed, N. G. Hadjiconstantinou and D. M. Parks |
|
|
We develop and perform continuum mechanics simulations of carbon nanotube (CNT) deployment directed by a combination of surface topography and rarefied gas flow. We employ the discrete elastic rods method to model the deposition of CNT as a slender elastic rod that evolves in time under two external forces, namely, van der Waals (vdW) and aerodynamic drag. Our results confirm that this self-assembly process is analogous to a previously studied macroscopic system, the “elastic sewing machine”, where an elastic rod deployed onto a moving substrate forms nonlinear patterns. In the case of CNTs, the complex patterns observed on the substrate, such as coils and serpentines, result from an intricate interplay between van der Waals attraction, rarefied aerodynamics, and elastic bending. We systematically sweep through the multidimensional parameter space to quantify the pattern morphology as a function of the relevant material, flow, and geometric parameters. Our findings are in good agreement with available experimental data. Scaling analysis involving the relevant forces helps rationalize our observations. Publications: |
| Instabilities of a flexible helical rod rotating in a viscous fluid
with: Khalid Jawed |
|

|
We combine experiments with simulations to investigate the fluid-structure interaction of a flexible helical rod rotating in a viscous fluid, under low Reynolds number conditions. Our analysis takes into account the coupling between the geometrically nonlinear behavior of the elastic rod with a nonlocal hydrodynamic model for the fluid loading. We quantify the resulting propulsive force, as well as the buckling instability of the originally helical filament that occurs above a critical rotation velocity. A scaling analysis is performed to rationalize the onset of this instability. A universal phase diagram is constructed to map out the region of successful propulsion and the corresponding boundary of stability is established. Comparing our results with data for flagellated bacteria suggests that this instability may be exploited in nature for physiological purposes. We also consider the case when the helical filament is simultaneously subjected to an axial flow. Under axial flow, and in the absence of rotation, the initially helical rod is extended. Above a critical flow speed its configuration comprises a straight portion connected to a localized helix near the free end. When the rod is also rotated about its helical axis, propulsion is only possible in a finite range of angular velocity, with an upper bound that is limited by buckling of the soft helix arising due to viscous stresses. A systematic exploration of the parameter space allows us to quantify regimes for successful propulsion for a number of specific bacteria. Publications: |
| The interplay between the mechanics and topology of elastic knots
with: Khalid Jawed, Peter Dieleman and Basile Audoly |
|

|
We combine experiments and theory to study the mechanics of overhand knots in slender elastic rods under tension. The equilibrium shape of the knot is governed by an interplay between topology, friction, and bending. We use precision model experiments to quantify the dependence of the mechanical response of the knot as a function of the geometry of the self-contacting region, and for different topologies as measured by their crossing number. An analytical model based on the nonlinear theory of thin elastic rods is then developed to describe how the physical and topological parameters of the knot set the tensile force required for equilibrium. Excellent agreement is found between theory and experiments for overhand knots over a wide range of crossing numbers. Publications: Press Coverage: |
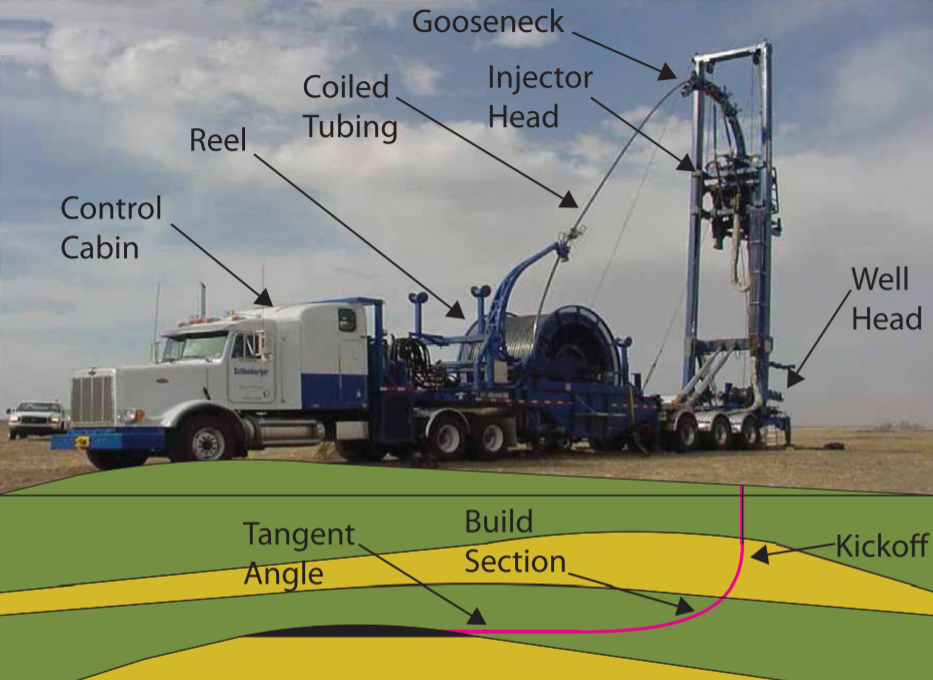
| Buckling of a rod inside a cylindrical constraint: Applications to coiled tubing operations
with: Jay Miller, Jahir Prabon and Nathan Wicks |
|
|
We present results of an experimental investigation of a new mechanism for extending the reach of an elastic rod injected into a horizontal cylindrical constraint, prior to the onset of helical buckling. This is accomplished through distributed, vertical vibration of the constraint during injection. A model system is developed that allows us to quantify the critical loads and resulting length scales of the buckling configurations, while providing direct access to the buckling process through digital imaging. In the static case (no vibration), we vary the radial size of the cylindrical constraint and find that our experimental results are in good agreement with existing predictions on the critical injection force and length of injected rod for helical buckling. When vertical vibration is introduced, reach can be extended by up to a factor of four, when compared to the static case. The injection speed (below a critical value that we uncover), as well as the amplitude and frequency of vibration, are studied systematically and found to have an effect on the extent of improvement attained. Image courtesy of Schlumberger-Doll Research. Publications: Press Coverage: |
| Coiling ‘spaghetti’ onto rigid substrates
with: Eitan Grinspun |
|

|
The deployment of a rodlike structure onto a moving substrate is commonly found in a variety engineering applications, from the fabrication of nanotube serpentines to the laying of submarine cables and pipelines. Predictively understanding the resulting coiling patterns is challenging given the nonlinear geometry of deposition. In this study, we combine precision model experiments with computer simulations tools and explore the mechanics of coiling. In particular, the natural curvature of the rod is found to dramatically affect the coiling process. We have introduced a computational framework that is widely used in computer animation into engineering, as a predictive tool for the mechanics of filamentary structures. This work was done in close collaboration with Eitan Grinspun’s Computer Graphics Group (Columbia University). [Introductory video about this study] Publications: Press Coverage: |
| The Mechanics of Curly Hair
with: Jay Miller, Arnaud Lazarus and Basile Audoly |
|


|
We tackle the deceivingly simple problem of a suspended naturally curved rod, which we consider as an analogue for curly hair, to predict its resulting shapes. The role of natural curvature in the mechanics of rods, as a control parameter, has been largely overlooked in the literature. In this study we seek to understand how natural curvature affects the configuration of a thin elastic rod suspended under its own weight. We combine precision desktop experiments, numerics, and theoretical analysis to explore the equilibrium shapes set by the coupled effects of elasticity, natural curvature, nonlinear geometry, and gravity. A phase diagram is constructed in terms of the control parameters of the system, namely the dimensionless curvature and weight, where we identify three distinct regions: planar curls, localized helices, and global helices. We analyze the stability of planar configurations, and describe the localization of helical patterns for long rods, near their free end. The observed shapes and their associated phase boundaries are then rationalized based on the underlying physical ingredients. Our framework is applicable to a variety of natural and engineered rodlike structures, over many length scales. Publications: Press Coverage: |
| Geometrically nonlinear configurations of thin elastic rods
with: Arnaud Lazarus and Jay Miller |
|

|
We have developed a novel continuation method to calculate the equilibria of elastic rods under large geometrically nonlinear displacements and rotations. To describe the kinematics we exploit the synthetic power and computational efficiency of quaternions. The energetics of bending, stretching and torsion are all taken into account to derive the equilibrium equations which we solve using an asymptotic numerical continuation method. This provides access to the full set of analytical equilibrium branches (stable and unstable), a.k.a bifurcation diagrams. This is in contrast with the individual solution points attained by classical energy minimization or predictor-corrector techniques. |
|
We challenge our numerics for the specific problem of an extremely twisted naturally curved rod and perform a detailed comparison against a precision desktop-scale experiments. The quantification of the underlying 3D buckling instabilities and the characterization of the resulting complex configurations are in excellent agreement between numerics and experiments. |
|
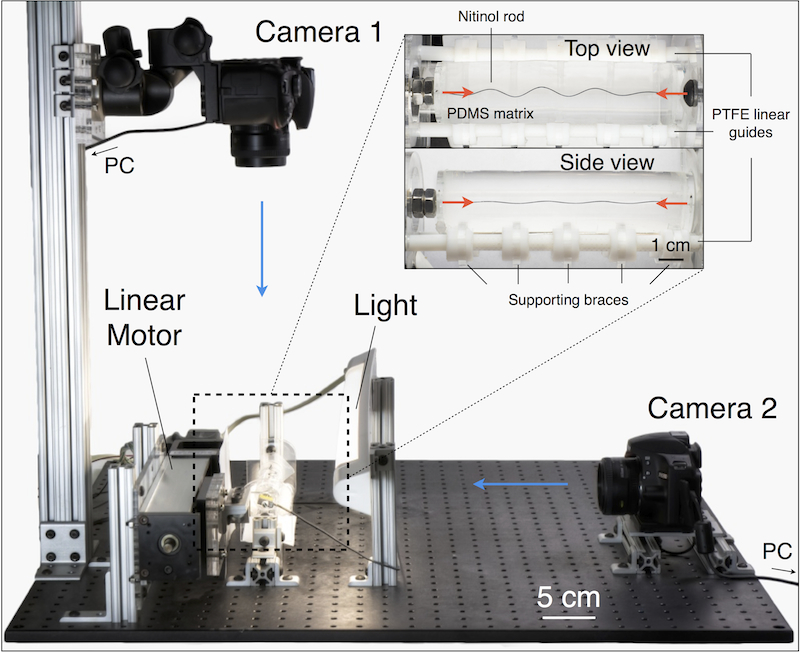
|
We have also studied the buckling of a slender rod embedded in a soft elastomeric matrix. In our experiments, depending on the control parameters, both planar wavy (2D) or non-planar coiled (3D) configurations are observed in the post-buckling regime. Our analytical and numerical results indicate that the rod buckles into 2D configurations when the compression forces associated to the two lowest critical modes are well separated. In contrast, 3D coiled configurations occur when the two buckling modes are triggered at onset, nearly simultaneously. We show that the separation between these two lowest critical forces can be controlled by tuning the ratio between the stiffness of the matrix and the bending stiffness of the rod, thereby allowing for specific buckling configurations to be target by design. Publications: |
