From viral capsids to architectural domes, slender shells are ubiquitous in natural and engineered structures. Their Mechanics is tightly intertwined with the underlying geometry and the onset for instability is a classic problem in structural Mechanics. At the flexLab, we have revived this old field by an innovative experimental approach that focuses on the postbuckling regime, where strong geometric nonlinearities and energy focusing can emerge. Central to this effort, we have devised a robust, versatile,and precise fabrication mechanism to rapid prototype thin shells in a lab setting. We are also interested in problems involving the large deformation of elastic plates, for example when loaded under aerodynamic or hydrodynamic conditions.
Topics that we have investigated on plates and shells include: predicting knock-down factor in the buckling of pressurized shells, periodic patterning of shell-substrate systems, form-finding in gridhells, stress-focusing in buckled shells and tearing of thin sheets. A more detailed account of these examples and other problems is provided below.
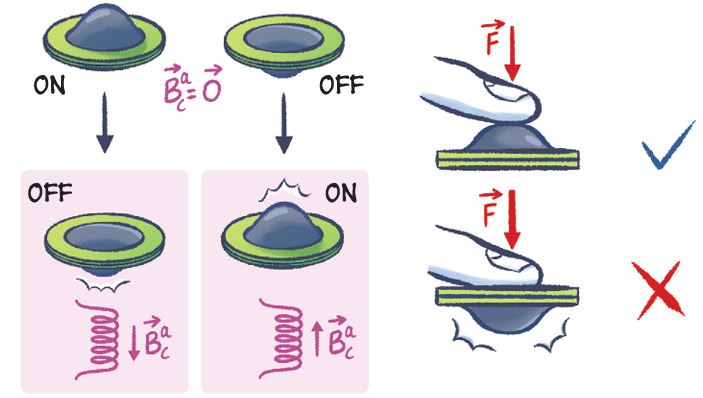
Leveraging the Snap Buckling of Bistable Magnetic Shells to Design a Refreshable Braille Dot
| with: Arefeh Abbasi, Tian Chen, and Bastien F. G. Aymon, |
 |
|
A design concept is proposed for the building block, a dot, of programmable Braille readers utilizing bistable shell buckling, magnetic actuation, and pneumatic loading. The design process is guided by Finite Element simulations, which are initially validated through precision experiments conducted on a scaled-up, single-shell model system. Then, the simulations are leveraged to systematically explore the design space, adhering to the standardized geometric and physical specifications of Braille systems. The findings demonstrate the feasibility of selecting design parameters that satisfy both geometric requirements and blocking forces under moderate magnetic fields, facilitated by pneumatic loading to switch between the two stable states. While the study is focused on experimentally validated numerical simulations, it also identifies several manufacturing challenges that need to be resolved for future physical implementations. Publications: |
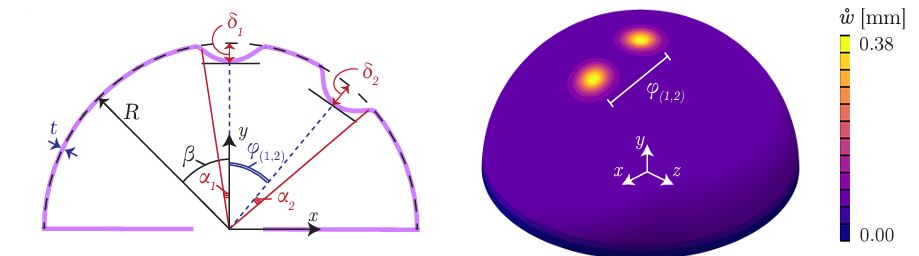
Defect-Defect Interactions in the Buckling of Imperfect Spherical Shells
| with: Fani Derveni, and Arefeh Abbasi |
 |
|
We perform finite element simulations to study the impact of defect-defect interactions on the pressure-induced buckling of thin, elastic, spherical shells containing two dimpled imperfections. Throughout, we quantify the critical buckling pressure of these shells using their knockdown factor. We examine cases featuring either identical or different geometric defects and systematically explore the parameter space, including the angular separation between the defects, their widths and amplitudes, and the radius-to-thickness ratio of the shell. As the angular separation between the defects is increased, the buckling strength initially decreases, then increases before reaching a plateau. Our primary finding is that the onset of defect-defect interactions, as quantified by a characteristic length scale associated with the onset of the plateau, is set by the critical buckling wavelength reported in the classic shell-buckling literature. Beyond this threshold, within the plateau regime, the buckling behavior of the shell is dictated by the largest defect. Publications: |
Probabilistic buckling of imperfect hemispherical shells containing a distribution of defects
| with: Fani Derveni, William Gueissaz, and Dong Yan |
 |
|
The buckling of spherical shells is highly sensitive to imperfections. Traditionally, imperfect shells are empirically characterized by the knockdown factor, which represents the ratio between the measured buckling strength and the predicted strength for a perfect shell. Recent advancements have shown that predicting the knockdown factor for a shell with a single imperfection is possible with detailed a priori knowledge of the defect geometry. However, addressing a similar issue for a shell with multiple defects remains an open question. In this study, we utilize finite element simulations, validated against precise experiments, to explore hemispherical shells containing a well-defined distribution of imperfections. Our objective is to analyze the statistics of the resulting knockdown factors. Initially, we focus on shells with only two defects, revealing non-trivial interaction regimes that echo findings in cylindrical shells. Subsequently, we create statistical ensembles of imperfect shells, with defect amplitudes sampled from a log-normal distribution. Our findings indicate that a 3-parameter Weibull distribution excellently describes the measured statistics of knockdown factors. This suggests that shell buckling can be viewed as an extreme-value statistics phenomenon. Publications: |
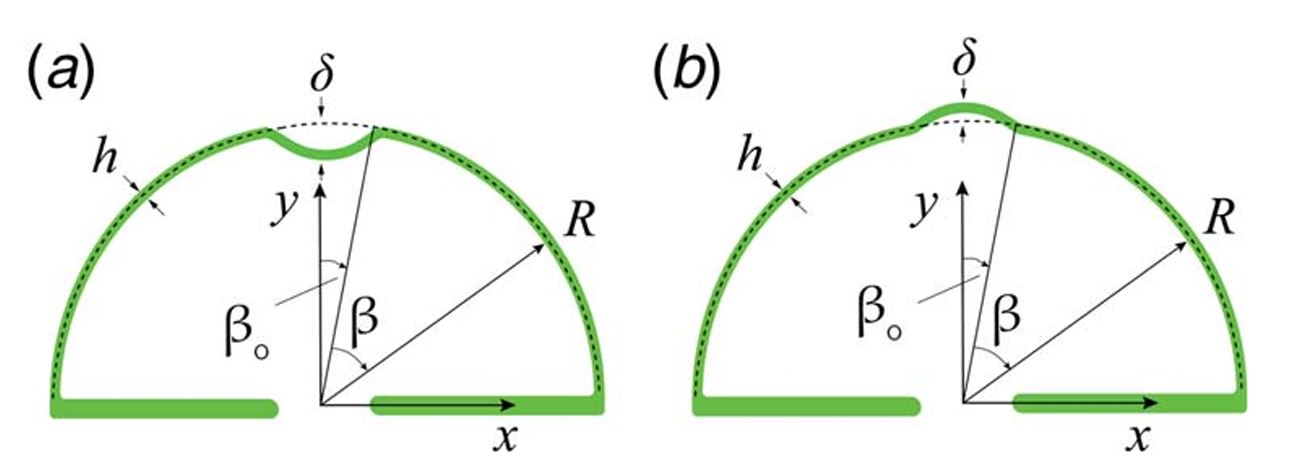
Comparing the Buckling Strength of Spherical Shells With Dimpled Versus Bumpy Defects
| with: Arefeh Abbasi, and Fani Derveni |
 |
|
We investigate the effect of defect geometry, indicating the sensitivity of the critical buckling conditions of spherical shells under external pressure loading. Specifically, we perform a comparative study between shells containing dimpled (inward) and bumpy (outward) Gaussian defects. The former has become the standard shape in many recent shell-buckling studies, whereas the latter has remained mostly unexplored. We employ finite-element simulations, previously validated against experiments, to compute the knockdown factors for the two cases. We systematically explore the parameter space of the defect geometry. For the same magnitudes of the amplitude and angular width of the defect, we find that shells containing bumpy defects consistently exhibit significantly higher knockdown factors than shells with the more classic dimpled defects. Furthermore, the relationship of the knockdown as a function of the amplitude and the width of the defect is qualitatively different between the two cases, which also exhibit distinct post-buckling behavior. A speculative interpretation of the results is provided based on the qualitative differences in the mean-curvature profiles of the two cases. Publications: |
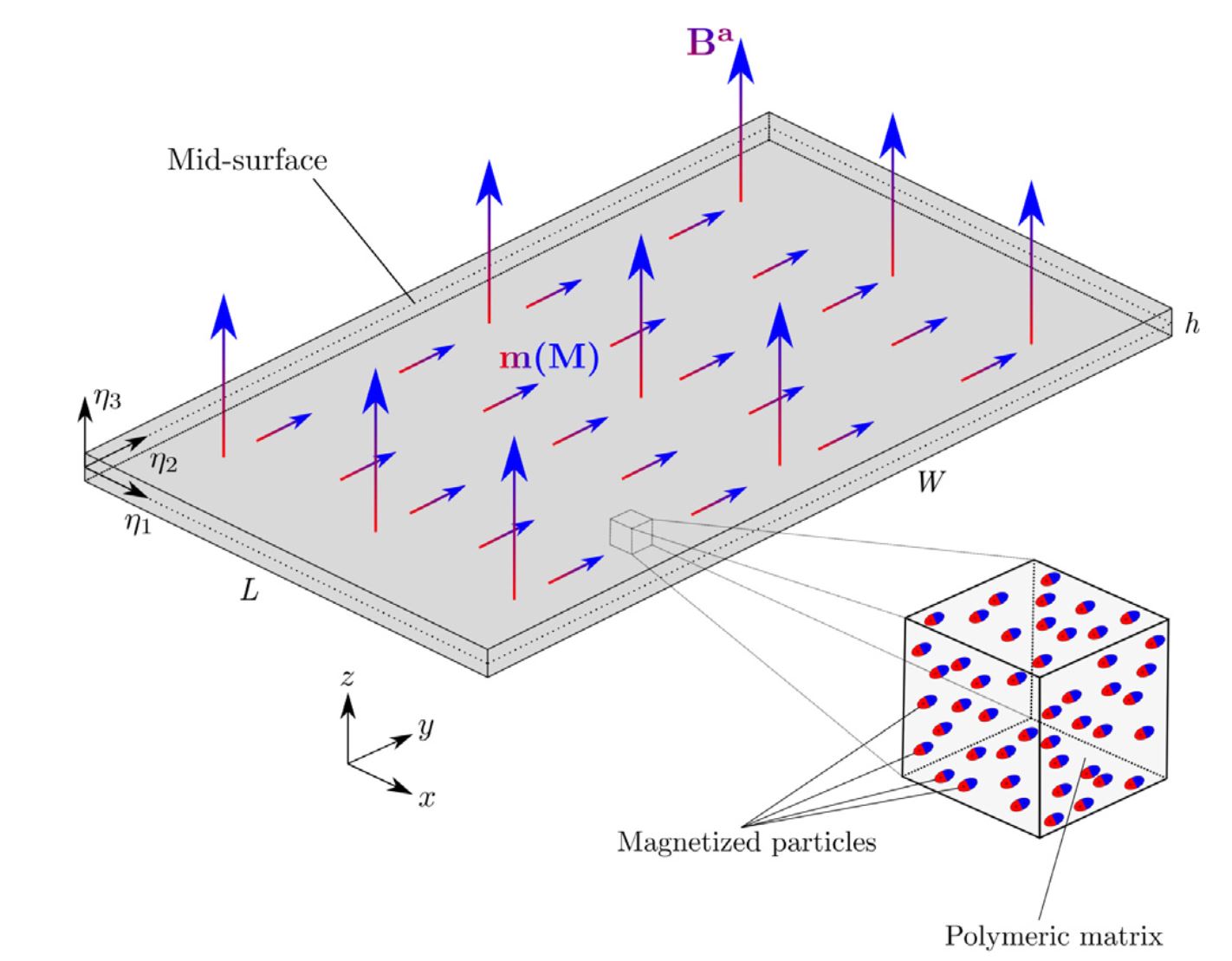
A reduced-order, rotation-based model for thin hard-magnetic plates
| with: Dong Yan and Bastien F. G. Aymon |
 |
|
We develop a reduced-order model for thin plates made of hard magnetorheological elastomers (hard-MREs), which are composed of hard-magnetic particles embedded in a polymeric matrix. First, we propose a new magnetic potential, as an alternative to an existing torque-based 3D continuum theory of hard-MREs, obtained by reformulating the remnant magnetization of a deformed hard-MRE body. Specifically, the magnetizations in the initial and current configurations are related by the rotation tensor decomposed from the deformation gradient, independently of stretching deformation, motivated by recently reported observations in microscopic homogenization simulations. Then, we derive a 2D plate model through the dimensional reduction of our proposed rotation-based 3D theory. For comparison, we also provide a second plate model derived from the existing 3D theory. Finally, we perform precision experiments to thoroughly evaluate the proposed 3D and 2D models on hard-magnetic plates under various magnetic and mechanical loading conditions. We demonstrate that our rotation-based modification of the magnetic potential is crucial in correctly capturing the behavior of plates subjected to an applied field aligned with the magnetization, and undergoing in-plane stretching. In all the tested cases, our rotation-based 3D and 2D models yield predictions in excellent quantitative agreement with the experiments and can thus serve as predictive tools for the rational design of hard-magnetic plate structures. Publications: |
| A geometrically exact model for thin magneto-elastic shells
with: Matteo Pezzulla and Dong Yan |
 |
|
We develop a reduced model for hard-magnetic, thin, linear-elastic shells that can be actuated through an external magnetic field, with geometrically exact strain measures. Assuming a reduced kinematics based on the Kirchhoff–Love assumption, we derive a reduced two-dimensional magneto-elastic energy that can be minimized through numerical analysis. In parallel, we simplify the reduced energy by expanding it up to the second order in the displacement field and provide a physical interpretation. Our theoretical analysis allows us to identify and interpret the two primary mechanisms dictating the magneto-elastic response: a combination of equivalent magnetic pressure and forces at the first order, and distributed magnetic torques at the second order. We contrast our reduced framework against a three-dimensional nonlinear model by investigating three test cases involving the indentation and the pressure buckling of shells under magnetic loading. We find excellent agreement between the two approaches, thereby verifying our reduced model for shells undergoing nonlinear and non-axisymmetric deformations. We believe that our model for magneto-elastic shells will serve as a valuable tool for the rational design of magnetic structures, enriching the set of reduced magnetic models. Publications: |
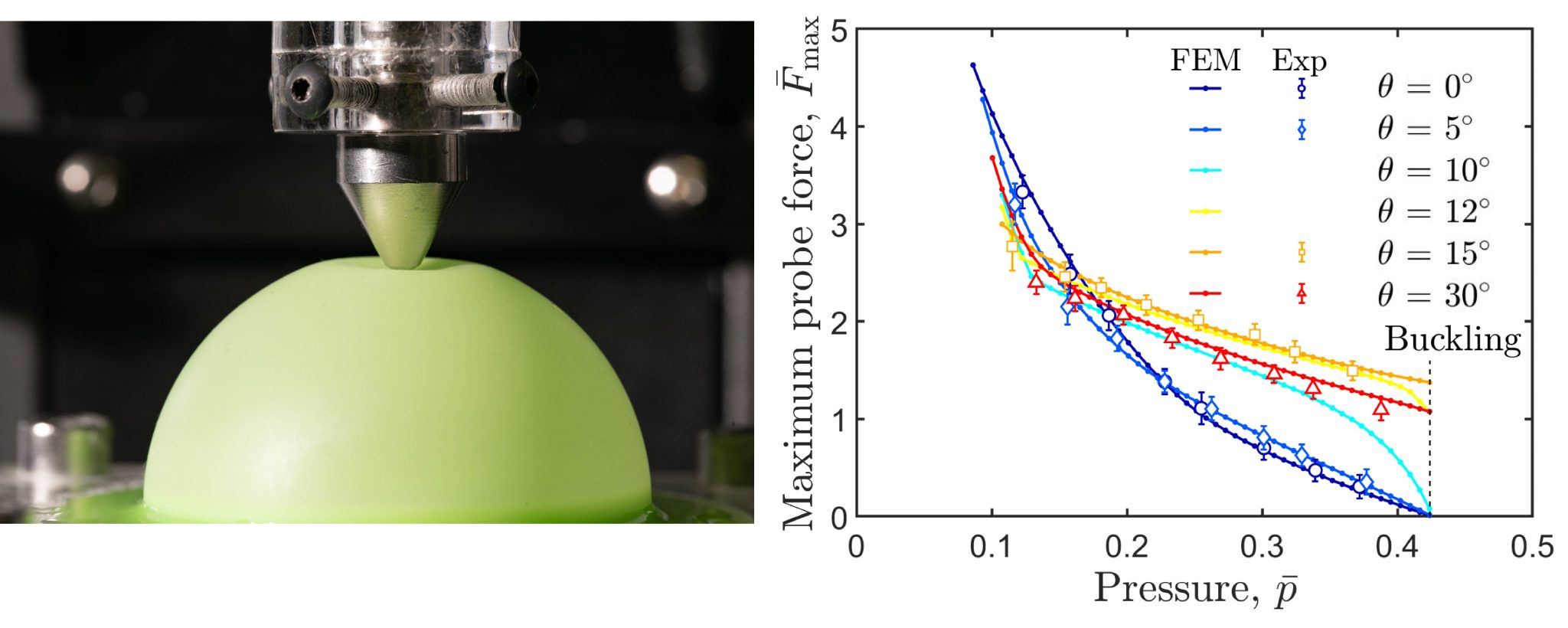
| Probing the buckling of pressurized spherical shells
with: Arefeh Abbasi and Dong Yan |
 |
|
The prediction of the critical buckling conditions of shell structures is plagued by imperfection sensitivity. Non-destructive testing through point-load probing has been recently proposed to map the stability landscape of cylindrical shells. However, the counterpart procedure for spherical shells is still debatable. Here, we focus on the mechanical response of pressurized spherical shells containing a single dimple-like defect to a point probe. Combining experiments, finite element modeling, and existing results from classic shell theory, we characterize the nonlinear force-indentation response of imperfect shells at different pressurization levels. From these curves, we seek to identify the critical buckling pressure of the shell. In particular, the indentation angle is varied systematically to examine its effect on the probing efficacy. We find that the critical buckling point can be inferred non-destructively by tracking the maxima of the indentation force–displacement curves, if the probe is implemented sufficiently close to the defect. When probing further away from the defect, the test fails in predicting the onset of buckling since the deformation due to indentation remains localized in the vicinity of the probe. Using FEM simulations and shallow shell theory, we quantify the characteristic length associated with this localized deformation due to indentation, both in the linear and nonlinear regimes. Our results demonstrate the limiting conditions of applicability for the usage of probing as a non-destructive technique to assess the stability of spherical shells. Publications: |
| Bending response of a book with internal friction
with: Samuel Poincloux, Tian Chen, and Basile Audoly |
 |
|
We study the bending of a booklike system, comprising a stack of elastic plates coupled through friction. The behavior of this layered system is rich and nontrivial, with a nonadditive enhancement of the apparent stiffness and a significant hysteretic response. A dimension reduction procedure is employed to develop a centerline-based theory describing the stack as a nonlinear planar rod with internal shear. We consider the coupling between the nonlinear geometry and the elasticity of the stacked plates, treating the interlayer friction perturbatively. This model yields predictions for the stack’s mechanical response in three-point bending that are in excellent agreement with our experiments. Remarkably, we find that the energy dissipated during deformation can be rationalized over 3 orders of magnitude, including the regimes of a thick stack with large deflection. This robust dissipative mechanism could be harnessed to design new classes of low-cost and efficient damping devices. Publications: |
| Magneto-active elastic shells with tunable buckling strength
with: Dong Yan, Matteo Pezzulla, Lilian Cruveiller, and Arefeh Abbasi |
 |
|
Shell buckling is central in many biological structures and advanced functional materials, even if, traditionally, this elastic instability has been regarded as a catastrophic phenomenon to be avoided for engineering structures. Either way, predicting critical buckling conditions remains a long-standing challenge. The subcritical nature of shell buckling imparts extreme sensitivity to material and geometric imperfections. Consequently, measured critical loads are inevitably lower than classic theoretical predictions. Here, we present a robust mechanism to dynamically tune the buckling strength of shells, exploiting the coupling between mechanics and magnetism. Our experiments on pressurized spherical shells made of a hard-magnetic elastomer demonstrate the tunability of their buckling pressure via magnetic actuation. We develop a theoretical model for thin magnetic elastic shells, which rationalizes the underlying mechanism, in excellent agreement with experiments. A dimensionless magneto-elastic buckling number is recognized as the key governing parameter, combining the geometric, mechanical, and magnetic properties of the system. Publications: |
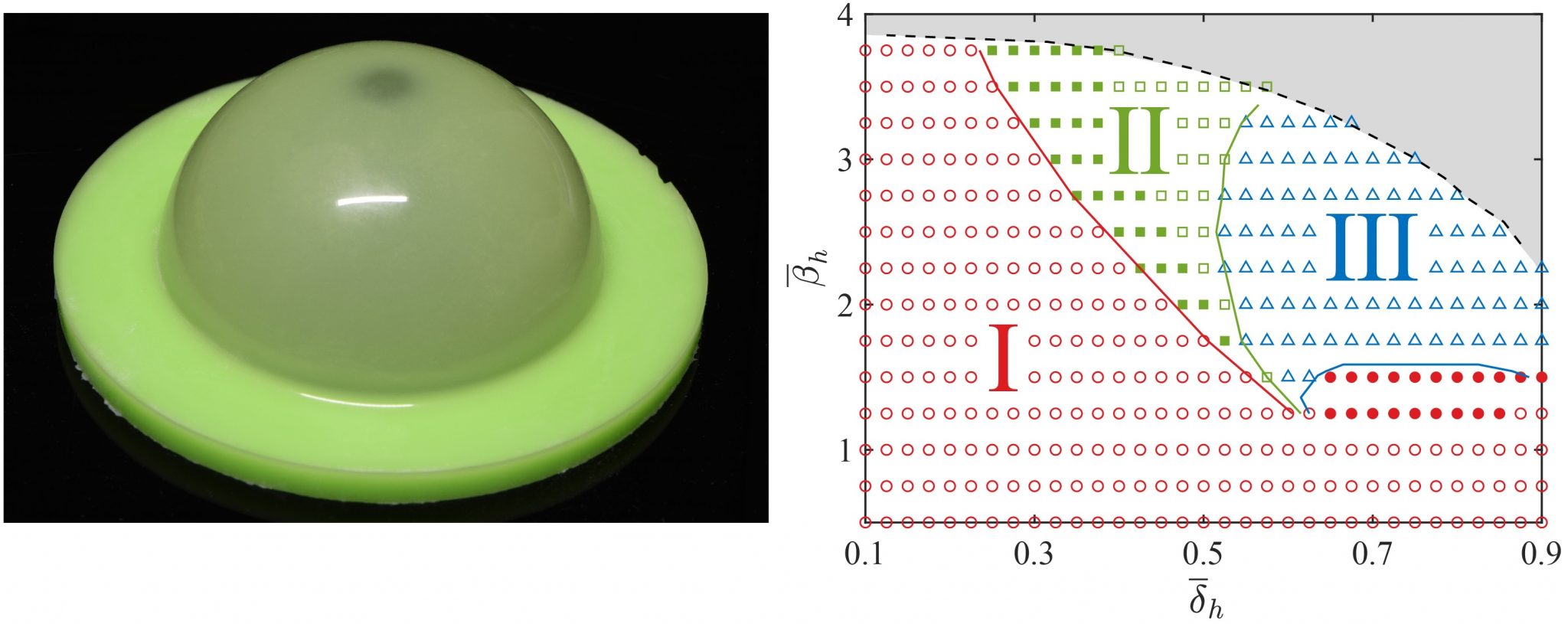
| Buckling of pressurized spherical shells containing a through-thickness defect
with: Dong Yan and Matteo Pezzulla |
 |
|
We present a study on the pressure buckling of thin, elastic spherical shells containing a thickness defect. Methodologically, we combine precision model experiments, finite element simulations, and a reduced axisymmetric shell model. We observe qualitatively different buckling behavior by varying the geometry of the defect: either one buckling event or two events comprising local buckling at the defect and global buckling of the entire shell. We systematically analyze the loading path for the imperfect shell under prescribed pressure or volume change and identify three buckling regimes. We then explore a wide parameter space to study the dependence of the buckling regimes on the defect geometry, thus obtaining a phase diagram with quantitative relationships between critical buckling pressures and defect geometry. We find that the global buckling becomes insensitive to the defect beyond a critical value of its amplitude, and we demonstrate that the buckling regimes are governed by the three geometric parameters of the defect, namely its width, amplitude and the width of the transition region across the edge of the defect. Publications: |
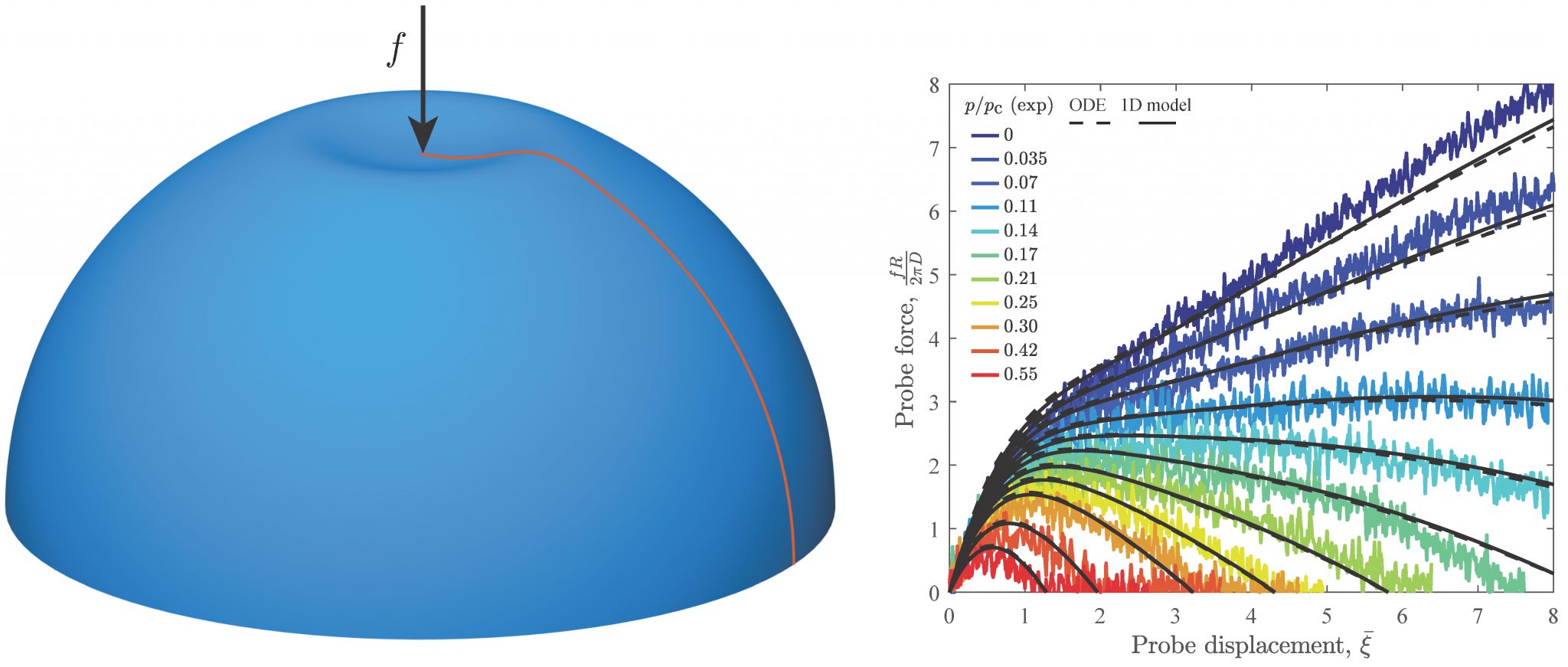
| A weak form implementation of nonlinear axisymmetric shell equations
with: Matteo Pezzulla |
 |
|
We present a weak form implementation of the nonlinear axisymmetric shell equations. This implementation is suitable to study the nonlinear deformations of axisymmetric shells, with the capability of considering a general mid-surface shape, non-homogeneous (axisymmetric) mechanical properties and thickness variations. Moreover, given that the weak balance equations are arrived to naturally, any external load that can be expressed in terms of an energy potential can, therefore, be easily included and modeled. We validate our approach with existing results from the literature, in a variety of settings, including buckling of imperfect spherical shells, indentation of spherical and ellipsoidal shells, and geometry-induced rigidity (GIR) of pressurized ellipsoidal shells. Whereas the fundamental basis of our approach is classic and well established, from a methodological view point, we hope that this brief note will be of both technical and pedagogical value to the growing and dynamic community that is revisiting these canonical but still challenging class of problems in shell mechanics. Publications: |
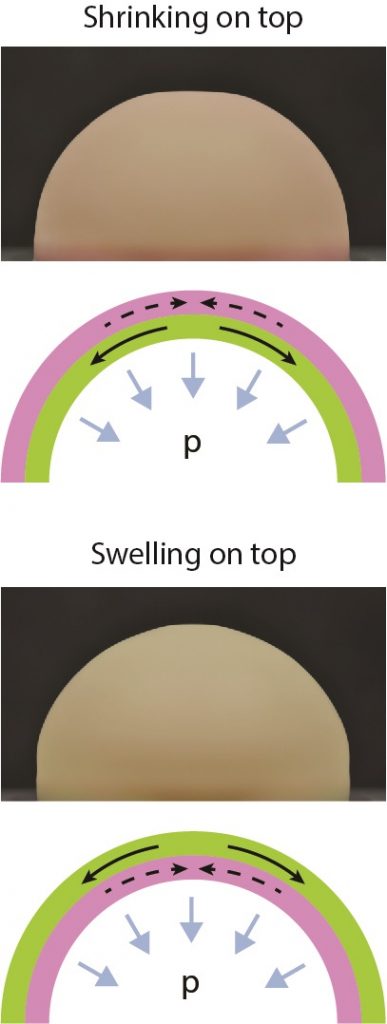
| Evolution of critical buckling conditions in imperfect bilayer shells
with: Anna Lee, Dong Yan, Matteo Pezzulla, and Douglas P. Holmes |
|
|
We propose and investigate a minimal mechanism that makes use of differential swelling to modify the critical buckling conditions of elastic bilayer shells, as measured by the knockdown factor. Our shells contain an engineered defect at the north pole and are made by two layers of different crosslinked polymers that exchange free molecular chains. Depending on the size of the defect and the extent of swelling, we can observe either a decreasing or increasing knockdown factor. FEM simulations are performed using a reduced model for the swelling process to aid us in rationalizing the underlying mechanism, providing a qualitative agreement with experiments. We believe that the working principle of our mechanism can be extended to bimetallic shells undergoing variations in temperature and to shells made by pH-responsive gels, where the change in knockdown factor could be changed dynamically. Publications: |
| Form finding in elastic gridshells
with: Changyeob Baek, Andrew O. Sageman-Furnas, and Mohammad K. Jawed |
|

|
Elastic gridshells comprise an initially planar network of elastic rods that are actuated into a shell-like structure by loading their extremities. The resulting actuated form derives from the elastic buckling of the rods subjected to inextensibility. We study elastic gridshells with a focus on the rational design of the final shapes. Our precision desktop experiments exhibit complex geometries, even from seemingly simple initial configurations and actuation processes. The numerical simulations capture this nonintuitive behavior with excellent quantitative agreement, allowing for an exploration of parameter space that reveals multistable states. We then turn to the theory of smooth Chebyshev nets to address the inverse design of hemispherical elastic gridshells. The results suggest that rod inextensibility, not elastic response, dictates the zeroth-order shape of an actuated elastic gridshell. As it turns out, this is the shape of a common household strainer. Therefore, the geometry of Chebyshev nets can be further used to understand elastic gridshells. In particular, we introduce a way to quantify the intrinsic shape of the empty, but enclosed regions, which we then use to rationalize the nonlocal deformation of elastic gridshells to point loading. This justifies the observed difficulty in form finding. Nevertheless, we close with an exploration of concatenating multiple elastic gridshell building blocks. We have also studied what sets the rigidity of elastic gridshells under point load indentation, finding scaling law in terms of the dimension of the structure and the number of the rods it contains, as well as the geometric and material properties of the individual rods. Our proposed empirical relation for the rigidity also points to the underlying nonlocal nature of the mechanical response of gridshells, in contrast to the local response of isotropic continuum shells. We further assess this nonlocality by quantifying the resulting radial displacement field as well as inspecting the effect of the location of the indentation point on the rigidity Publications: • C. Baek and P.M. Reis, “Rigidity of hemispherical elastic gridshells under point load indentation” Journal of the Mechanics and Physics of Solids, 124, 411-426 (2019). [html, pdf]. |
| Buckling patterns in biaxially pre-stretched bilayer shells
with: Rashed Al-Rashed, Francisco López Jiménez, and Joel Marthelot |
|
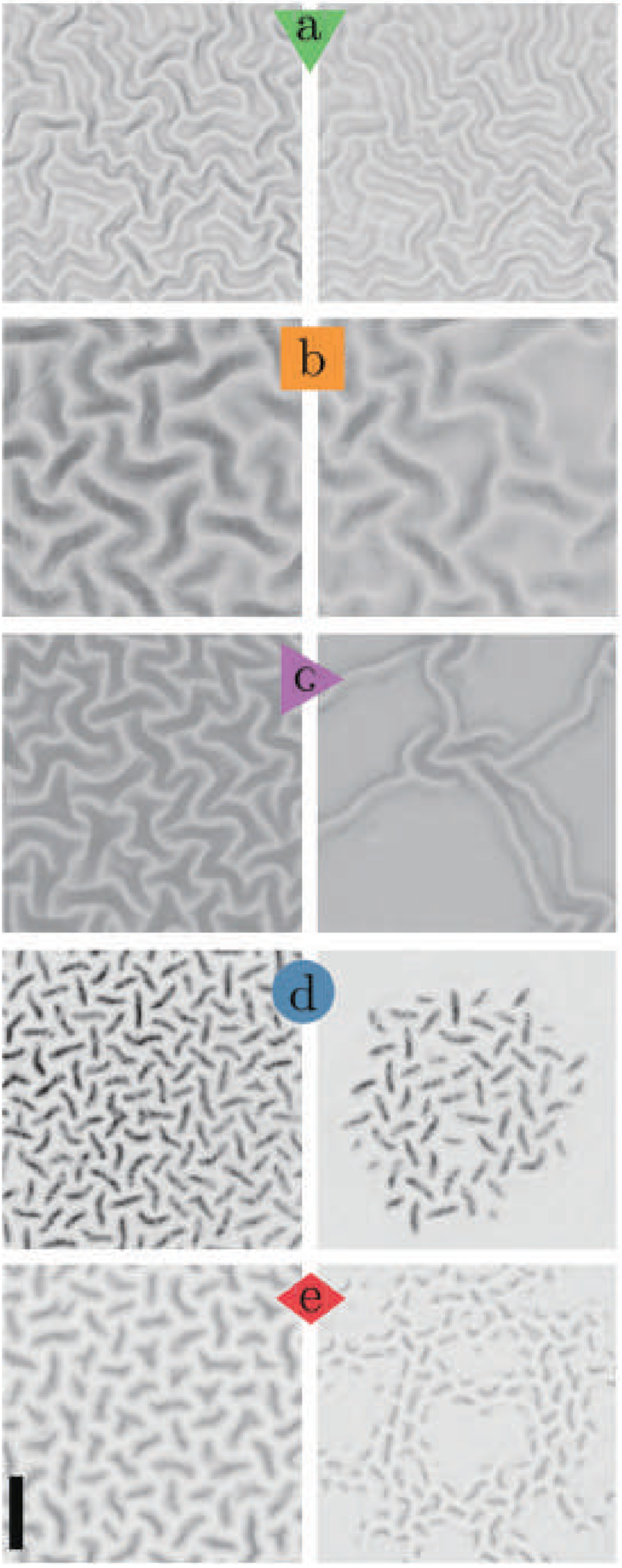
|
We introduce a new experimental system to study the effects of pre-stretch on the buckling patterns that emerge from the biaxial compression of elastomeric bilayer shells. Upon fabrication of the samples, releasing the pre-stretch in the substrate through deflation places the outer film in a state of biaxial compression and yields a variety of buckling patterns. We systematically explore the parameter space by varying the pre-stretch of the substrate and the ratio between the stiffness of the substrate and film. The phase diagram of the system exhibits a variety of buckling patterns: from the classic periodic wrinkle to creases, folds, and high aspect ratio ridges. Our system is capable of readily transitioning between these buckling patterns, a first for biaxial systems. We focus on the wrinkle to ridge transition. In the latter, we find that pre-stretch plays an essential role and that the ridge geometry (width, height) remains nearly constant throughout their formation process. For the localized ridged patterns, we find that the propagation of the ridge tip depends strongly on both strain and stiffness ratio, in a way that is akin to hierarchical fracture. We have also studied what sets the rigidity of elastic gridshells under point load indentation, finding scaling law in terms of the dimension of the structure and the number of the rods it contains, as well as the geometric and material properties of the individual rods. Our proposed empirical relation for the rigidity also points to the underlying nonlocal nature of the mechanical response of gridshells, in contrast to the local response of isotropic continuum shells. We further assess this nonlocality by quantifying the resulting radial displacement field as well as inspecting the effect of the location of the indentation point on the rigidity Publications: |
| Reversible patterning of spherical shells through constrained buckling
with: Joel Marthelot, Pierre-Thomas Brun, and Francisco López Jiménez |
|


|
Recent advances in active soft structures envision the large deformations resulting from mechanical instabilities as routes for functional shape-morphing. Numerous such examples exist for filamentary and plate systems. However, examples with double-curved shells are rarer, with progress hampered by challenges in fabrication and the complexities involved in analyzing their underlying geometrical nonlinearities. We show that on-demand patterning of hemispherical shells can be achieved through constrained buckling. Their post-buckling response is stabilized by an inner rigid mandrel. Through a combination of experiments, simulations and scaling analyses, our investigation focuses on the nucleation and evolution of the buckling patterns into a reticulated network of sharp ridges. The geometry of the system, namely the shell radius and the gap between the shell and the mandrel, is found to be the primary ingredient to set the surface morphology. This prominence of geometry suggests a robust, scalable, and tunable mechanism for reversible shape-morphing of elastic shells. Videos that summarize this project can be found in the following links [Video1] [Video2]. Publications: |
| Imperfection sensitivity: Critical buckling pressure of precisely imperfect shells
with: Anna Lee, Francisco López Jiménez, Joel Marthelot, and John W. Hutchinson |
|


|
We study the effect of a dimplelike geometric imperfection on the critical buckling load of spherical elastic shells under pressure loading. This is a canonical problem in Structural Mechanics that has been longstanding for more than 50 years. Our investigation combines precision experiments, finite element modeling, and numerical solutions of a reduced shell theory, all of which are found to be in excellent quantitative agreement. In the experiments, the geometry and magnitude of the defect can be designed and precisely fabricated through a customizable rapid prototyping technique. Our primary focus is on predictively describing the imperfection sensitivity of the shell to provide a quantitative relation between its knockdown factor and the amplitude of the defect. In addition, we find that the buckling pressure becomes independent of the amplitude of the defect beyond a critical value. The level and onset of this plateau are quantified systematically and found to be affected by a single geometric parameter that depends on both the radius-to-thickness ratio of the shell and the angular width of the defect. To the best of our knowledge, this is the first time that experimental results on the knockdown factors of imperfect spherical shells have been accurately predicted, through both finite element modeling and shell theory solutions. A video that summarizes this project can be found in the following link [Video]. This project was done in collaboration with John Hutchinson (Harvard University). Publications: |
| Rapid fabrication of slender elastic shells
with: Anna Lee, Pierre-Thomas Brun, Joel Marthelot, Gioele Balestra, and François Gallaire |
|

|
Various manufacturing techniques exist to produce double-curvature shells, including injection, rotational and blow molding, as well as dip coating. However, these industrial processes are typically geared for mass production and are not directly applicable to laboratory research settings, where adaptable, inexpensive and predictable prototyping tools are desirable. In this project we have studied the rapid fabrication of hemispherical elastic shells by coating a curved surface with a polymer solution that yields a nearly uniform shell, upon polymerization of the resulting thin film. We experimentally characterize how the curing of the polymer affects its drainage dynamics and eventually selects the shell thickness. The coating process is then rationalized through a theoretical analysis that predicts the final thickness, in quantitative agreement with experiments and numerical simulations of the lubrication flow field. This robust fabrication framework should be invaluable for future studies on the mechanics of thin elastic shells and their intrinsic geometric nonlinearities. A video that summarizes this project can be found in the following link [Video]. This project was done in collaboration with the group of François Gallaire at EPFL (Switerzland). Publications: Press coverage: |
| Mechanics of thin elastic shells: Geometry-Induced Rigidity and Localization
with: Arnaud Lazarus, Bastiaan Florijn, Amin Ajdari and Ashkan Vaziri |
|
|
We have introduced a predictive framework for the rigidity of thin elastic shells which can also account for the situation when the shell is over-pressurized. Our concept of Geometry-Induced Rigidity can be used in reverse, as a precision non-destructive tool, to measure parameters of a shell (e.g. thickness) upon knowing the geometry of the underlying surface and the local mechanical response. The scale-invariance of Geometry-Induced Rigidity suggests that our framework should find uses across length scales: from the mechanical testing of viral capsids through Atomic Force Microscopy, to ocular tonometry procedures or in the design of architectural shells. All this work was inspired by the remarkable physics of an elegant eggshell! |
|

|
More recently, we have been studying the emergence and evolution of point and linear-like loci of localization on thin shells indented well into the nonlinear regime. For large enough indentation, sharp points of localized curvature form, which we refer to as ‘s-cones’ (for shell-cones), in contrast with their developable cousins in plates, ‘d-cones’. Through experiments and FEM, e have found that the shape of the indenter has a significant effect on the mechanical response and that there is a qualitative different between sharp and blunt indenters. Given the importance of geometry and the scale-invariance of this problem, our results should find uses at the microscale, e.g. for AFM, where it is crucial to understand how the curvature of the tip, relative to the object being indented, affects the mechanical response. Videos of S-cones of a thin shell under indentation: [Experiments, FEM Simulations] Publications: Press coverage: |
| The Buckliball and Buckligami: buckling-induced encapsulation and soft Actuation
with: Jongmin Shim, Elizabeth Chen, Claude Perdigou and Katia Bertoldi |
|

|
We introduce a class of continuum shell structures, the Buckliball, which undergoes folding induced by buckling under pressure loading. The geometry of the Buckliball consists of a spherical shell patterned with a regular array of circular voids. Topological constraints set that the possible number and arrangement of these voids are found to be restricted to five and only five specific configurations. Below a critical internal pressure, the narrow ligaments between the voids buckle, leading to a cooperative buckling cascade of the skeleton of the ball. This leads to closure of the voids and a reduction of the total volume of the shell by up to 54\%, while remaining spherical, thereby opening the possibility of encapsulation. Mechanical instabilities, which are often associated with failure in engineering, are here turned into an asset for functionality. |

|
In a separate study, we have introduced a new class of soft actuators based on the auxetic behavior of patterned cylindrical shells containing a layout of voids that can be designed to reversibly achieve flexural or twisting motion. Depressurizing our samples allows for tunable and controllable motion. Given that the deformation is primarily governed by the geometry of the design, coupled to the buckling of the thin ligaments of the pattern, the resulting modes of actuation should be readily scalable. Publications: Press coverage: |
| Wrinklons as Building-blocks in Wrinkling Cascades: From Curtains to Graphene Sheets |
|

|
We show that thin sheets under boundary confinement spontaneously generate a universal self-similar hierarchy of wrinkles. From simple geometry arguments and energy scalings, we develop a formalism based on wrinklons (the transition zones in the merging of two wrinkles) as building-blocks of the global pattern. Contrary to the case of crumpled paper where elastic energy is focused, this transition is described as smooth in agreement with a recent numerical work by B. Davidovich et al. This formalism is validated through experiments from hundreds of nm for graphene sheets to meters for ordinary curtains, which shows the universality of our description. We finally describe the effect of an external tension to the distribution of the wrinkles. Publications: Press coverage: |
| Rolling of Flexible Ribbons
with: Pascal Raux, John Bush and Christophe Clanet |
|
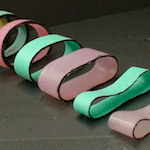
|
Galileo’s study of rigid spheres rolling down an inclined ramp is often considered as the starting point of modern physics, since it involves both theory and experiment. In this study we consider a variant of Galileo’s problem in which the ramp is rigid but the rolling body, an elastic cylindrical shell, is thin, flexible and therefore deformable. Particular attention is given to characterizing the steady shapes that arise in static and dynamic rolling configurations. In both cases, above a critical value of the forcing (either gravitational or centrifugal), the ribbon assumes a two-lobed peanut shape. Our theoretical model allows us to rationalize the observed shapes through consideration of the ribbon’s bending and stretching in response to the applied forcing. This dynamical elastic problem presents some common features with the rolling of a liquid drop on a hydrophobic surface or a lubricated ramp. Publications: Press coverage: |
| Delamination of thin films from an elastic substrate
with: Dominic Vella, Benoit Roman, José Bico and Arezki Boudaoud |
|

|
The wrinkling and delamination of stiff thin films adhered to a polymer substrate have important applications in `flexible electronics’. The resulting periodic structures, when used for circuitry, have remarkable mechanical properties since stretching or twisting of the substrate is mostly accommodated through bending of the film, which minimizes fatigue or fracture. To date, applications in this context have used substrate patterning to create an anisotropic substrate-film adhesion energy, thereby producing a controlled array of delamination `blisters’. However, even in the absence of such patterning, blisters appear spontaneously, with a characteristic size. Here, we perform well-controlled experiments at macroscopic scales to study what sets the dimensions of these blisters in terms of the material properties and explain our results using a combination of scaling and analytical methods. As well as pointing to a novel method for determining the interfacial toughness our analysis suggests a number of design guidelines for the thin films used in flexible electronic applications. Crucially, we show that to avoid the possibility that delamination may cause fatigue damage, the thin film thickness must be greater than a critical value, which we determine. [Video here] Publications: Press coverage: |

