When quantum effects are important and must be included in calculations, the computational time grows enormously. Efficient numerical algorithms are therefore essential. We have achieved speedups by orders of magnitude compared to simpler methods in the following areas:
Imaginary-time nonuniform mesh method for solving the multidimensional Schroedinger equation: Fermionization and melting of quantum Lennard-Jones crystals
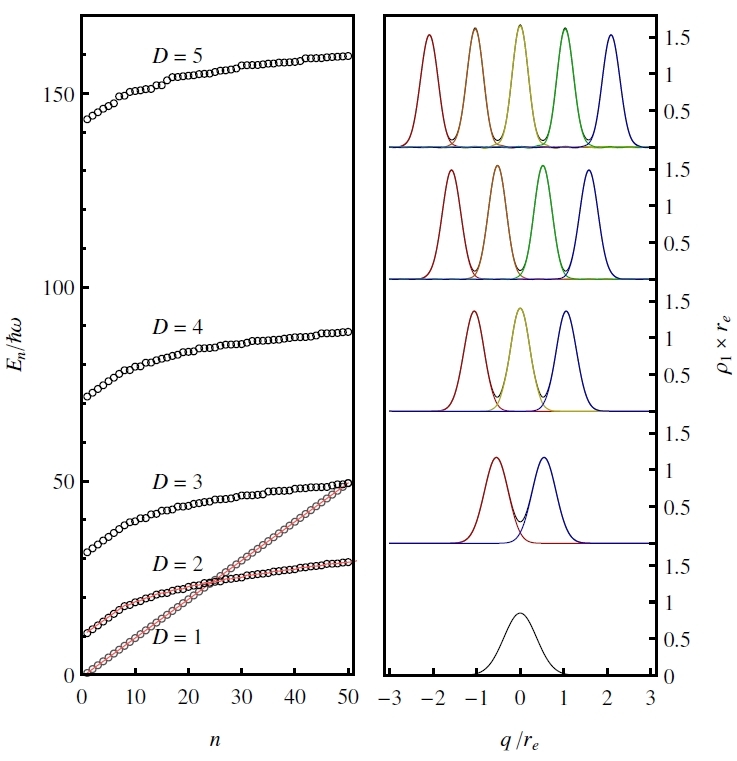
An imaginary-time nonuniform mesh method is presented and used to find the first 50 eigenstates and energies of up to five strongly interacting spinless quantum Lennard-Jones particles trapped in a one-dimensional harmonic potential. We show that the use of tailored grids reduces drastically the computational effort needed to diagonalize the Hamiltonian and results in a favorable scaling with dimensionality. Solutions to both bosonic and fermionic counterparts of this strongly interacting system are obtained, the bosonic case clustering as a Tonks-Girardeau crystal exhibiting the phenomenon of fermionization. The numerically exact excited states are used to describe the melting of this crystal at finite temperature.
|
|
This Figure shows the first 50 states of an ensemble of up to five Lennard-Jones (LJ) spinless particles trapped in a one-dimensional harmonic potential in the Tonks-Girardeau regime (Hernando and Vanicek 2013). Other systems—as ligh nucleii in molecules or quantum particles in porous media—can be also solved by our method, where the high number of excited states obtained can be used to solve dynamical problems with experimental and industrial interest. |
Role of sampling in evaluating classical time autocorrelation functions
Trajectory-based methods for computing time correlation function may become too expensive in many-dimensional systems. Yet, dimensionality-independent algorithms have been found for special correlation functions, such as classical and semiclassical fidelity. We explore how these correlations functions can be computed more efficiently in general. In a recent work (Zimmermann and Vanicek 2013), we proposed a sampling weight for which the number of trajectories needed for convergence of any classical autocorrelation function is independent of dimensionality of both the phase space and of the studied observable.
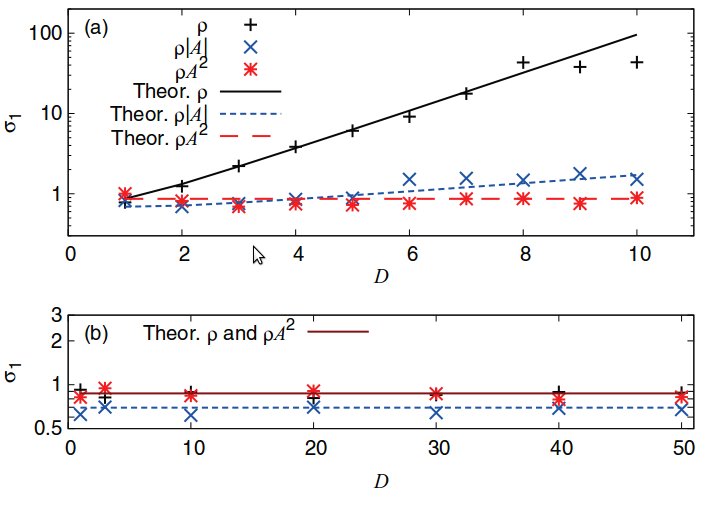
The above figure shows the expected statistical error per trajectory of the autocorrelation function of a function A in a D-dimensional. (a) A=q1q2···qD. Statistical error is independent of dimensionality for the algorithm with weight W=ρA2 and grows exponentially with D for the standard weight W=ρ as well for W=ρ|A|. In (b) A=μ·q, where μ is a D-dimensional vector. Statistical error is independent of dimensionality for all three weights.
Semiclassical method scaling independently of dimensionality
There is a controversy about scaling of semiclassical methods with dimensions: some believe that it is polynomial, while others have demonstrated an exponential scaling in special cases. We have proven rigorously that a semiclassical method can actually scale independently of dimensions (Mollica and Vanicek 2011). More precisely, we have shown that the expected number of trajectories required for the convergence of the Dephasing Representation is independent of the number of degrees of freedom (Mollica and Vanicek 2011). We do not know of any other semiclassical method with this property. This is demonstrated in the figure below showing the dependence of the statistical error on the number D of dimensions. The analytical predictions are compared with numerical tests for the DR as well as four classical (CL) methods (which are discussed in more detail below):
 |
We have further accelerated the method by combining it with the idea of Heller’s Cellular Dynamics and obtained the so-called Cellular Dephasing Representation (Sulc and Vanicek 2012).
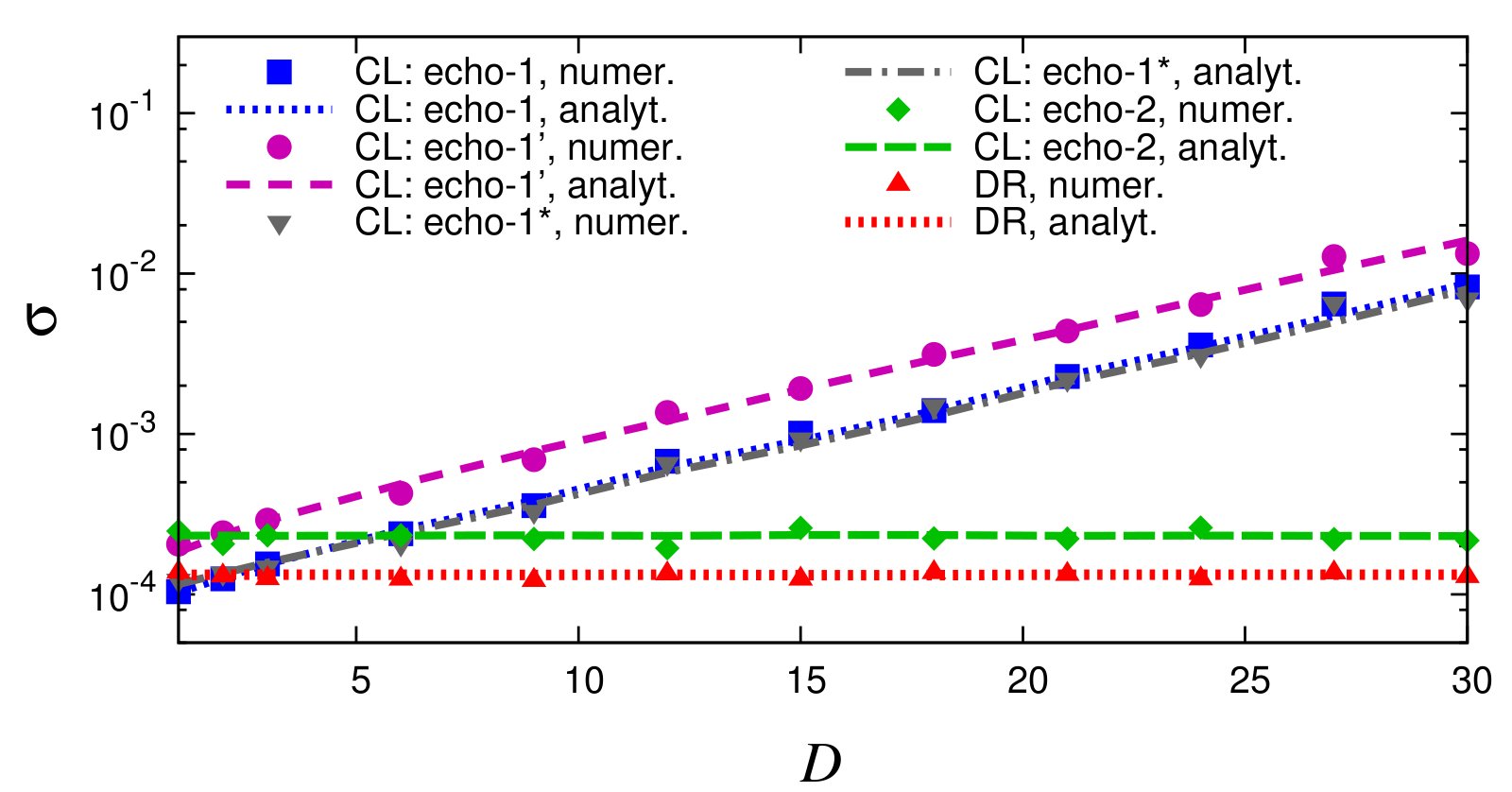
Classical fidelity algorithm scaling independently of dimensionality
We have shown that the number of trajectories required in all previously used algorithms for classical fidelity scales exponentially with the number of degrees of freedom. Then we have derived an algorithm for which the number of trajectories is independent of dimensionality and proven this property analytically [25]. The figure above shows the dependence of the statistical error on the number D of dimensions for three algorithms scaling exponentially with D (echo-1, echo-1′, and echo-1*) as well as our new algorithm (echo-2) scaling independently of D.
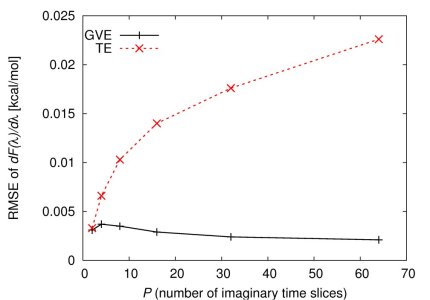
Efficient estimators in path integral calculations
In the area of chemical kinetics and thermodynamics, we are interested in full quantum calculations of of the equilibrium and kinetic isotope effects. The methods used are path integral Monte Carlo (PIMC) and path integral molecular dynamics (PIMD). In both methods, as one approaches the quantum limit, it is necessary to increase the number P of imaginary time slices in the path integral. In both PIMC and PIMD simulations, the statistical error of a computed quantity depends in general on P and the estimator. We have achieved significant speedups in both applications, by using the generalized virial estimator (GVE) instead of the thermodynamic estimator (TE) (Vanicek and Miller 2007,Zimmermann and Vanicek 2009). The figure below, from Ref. (Zimmerman and Vanicek 2009) gives a justification: it shows that the RMS error of the GVE (for a free energy derivative) is independent of P, making it easier to reach the quantum limit.