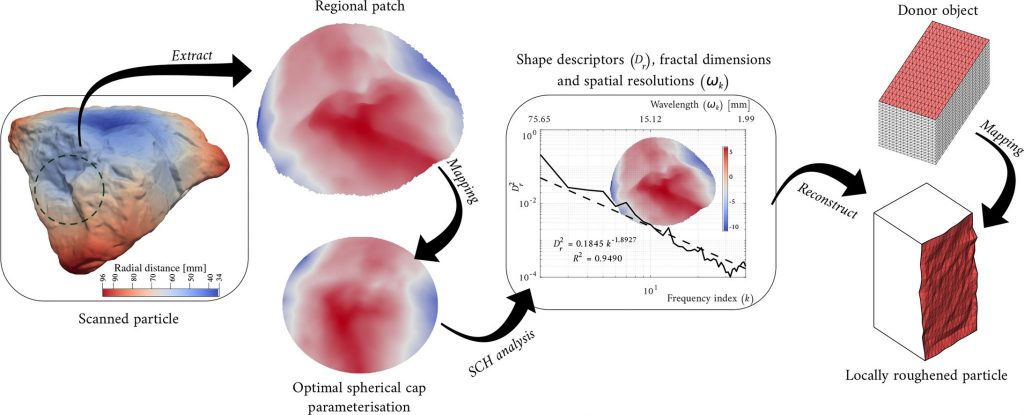
The field of granular material mechanics delves into the interactions among particles under diverse loading conditions, where factors such as particle shape, size, and material properties exhibit significant variability. Due to this complexity, numerical models are frequently employed to explore the influence of particle morphology and the resulting microstructures on a material’s mechanical behavior. Analogous challenges arise in structural engineering, particularly in the modeling of microstructures, such as in concrete aggregates or the constituent stones in stone masonry elements. Here, the shape and surface texture of the particles play a pivotal role in determining the properties of the composite matrices. In this study, we introduce a novel approach for analyzing the morphology of open surface patches using Spherical Cap Harmonics (SCH), with a particular focus on nominally flat patches, such as those where the global curvature radius approaches infinity. Our newly developed Spherical Cap Harmonic Analysis (SCHA) method enables the examination of the structure of any arbitrary surface patch more efficiently than traditional Spherical Harmonic Analysis (SHA). It achieves faster convergence, scales to varying levels of detail, and maintains reasonable computational complexity. This method is not only effective for reconstructing surfaces and altering the morphology of digital twins of real surfaces but also proves valuable in the numerical investigation of contact problems, including friction. Moreover, the use of orthogonal basis functions in our approach permits power spectral analyses of the coefficients derived from SCHA, facilitating the estimation of the fractal dimensions of the surfaces.
- Article:
- Spherical cap harmonic analysis (SCHA) for characterising the morphology of rough surface patches [journal link]
- Source code: [source code link]
- Dataset: [dataset link]
- Funding: This work was partially funded by the Swiss National Science Foundation.