Modeling of dynamic failure and fragmentation in brittle and quasi-brittle materials is still a challenge since it highly depends on the material micro-structure. Indeed, to be able to model flaws at the micro-structure scale, a fine description of the material is needed, and thus powerful and effective numerical methods. The finite elements method with dynamic insertion of cohesive elements is used, in order to take advantage of a higher computational efficiency than that of particle methods. Interaction among fragments is then handled by means of contact detection and contact laws algorithms.
Depending on the loading rate and on material parameters, convergence may constitute a numerical challenge. Simulations on very fine meshes require high amount of memory and efficiency, that only a parallel implementation of the algorithms together with high performance computing can supply.
All the code developed for this project is contained in our C++ library Akantu.
Dynamic failure
Failure of a civil engineering concrete structure under dynamic loading is a phenomenon which highly depends on the heterogeneous material composition. Concrete is a brittle like material which fractures via the nucleation, propagation and coalescence of local microcracks. Furthermore the rough surfaces of the generated macrocracks might enter in contact being responsible for the shear forces which can be transferred between the two cracks determining a part of the strength of the macrostructure.
The material microstructure of concrete plays then an important role in the failure processes. The wide kaleidoscope of sizes of the ingredients presents in the mixture defines the mechanical behavior. Concrete can be then modeled using a meso-mechanical approach in which aggregates and mortar are represented explicitly. Both continuum phases are considered to behave elastically, while nucleation, coalescence and propagation of cracks are modeled using the cohesive-element approach. Using a rigorous and scalable three-dimensional approach, the evolution of microcracks is simulated in a realistic manner.
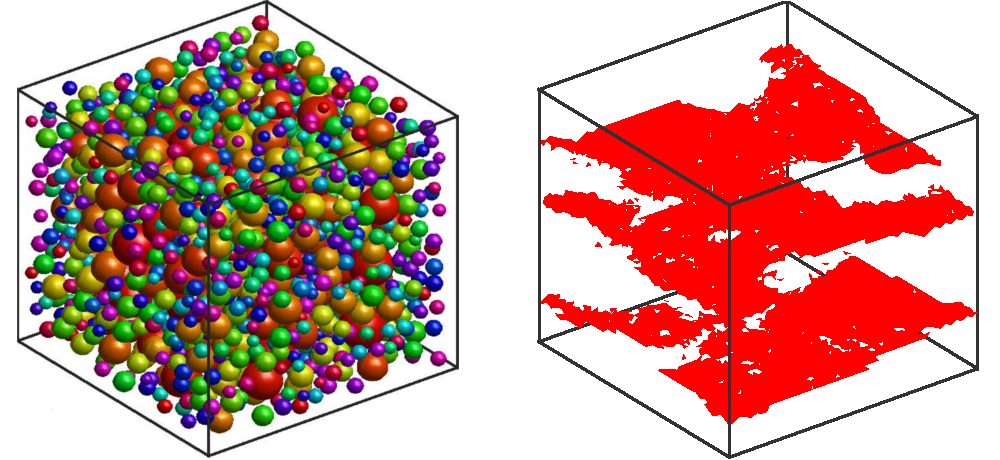
Figure: A cubic concrete model at the mesoscale and crack formation under tensile loading with a strain rate 10 /s.
Fragmentation
Fragmentation is a topic of major industrial (blast protection, mining, tunneling) as well as astrophysics (asteroid impacts) interest. Our focus is on fragmentation due to impacts, high-strain rate loads, and internal residual stresses. We conduct massively parallel simulations aiming at representing accurately cracks initiation, propagation, branching and interaction, as well as providing a detailed description of fragment sizes and velocities. Such simulations give us access to rapidly evolving fields and values (such as kinetic, potential, and dissipated energies) that cannot be accurately monitored during experimental tests, thus facilitating the understanding of the fragmentation process. Also, fragment statistics (their sizes, masses, velocities) can be derived. From these outputs, we can investigate the fragment mass and velocity global distributions and understand their correlations.

Figure: Fragments identified by fully damaged cohesive elements in two tempered glass plates 8 mm thick with different residual stress values.
Figure: Fragments identified by fully damaged cohesive elements in two tempered glass plates 8 mm thick with different residual stress values.
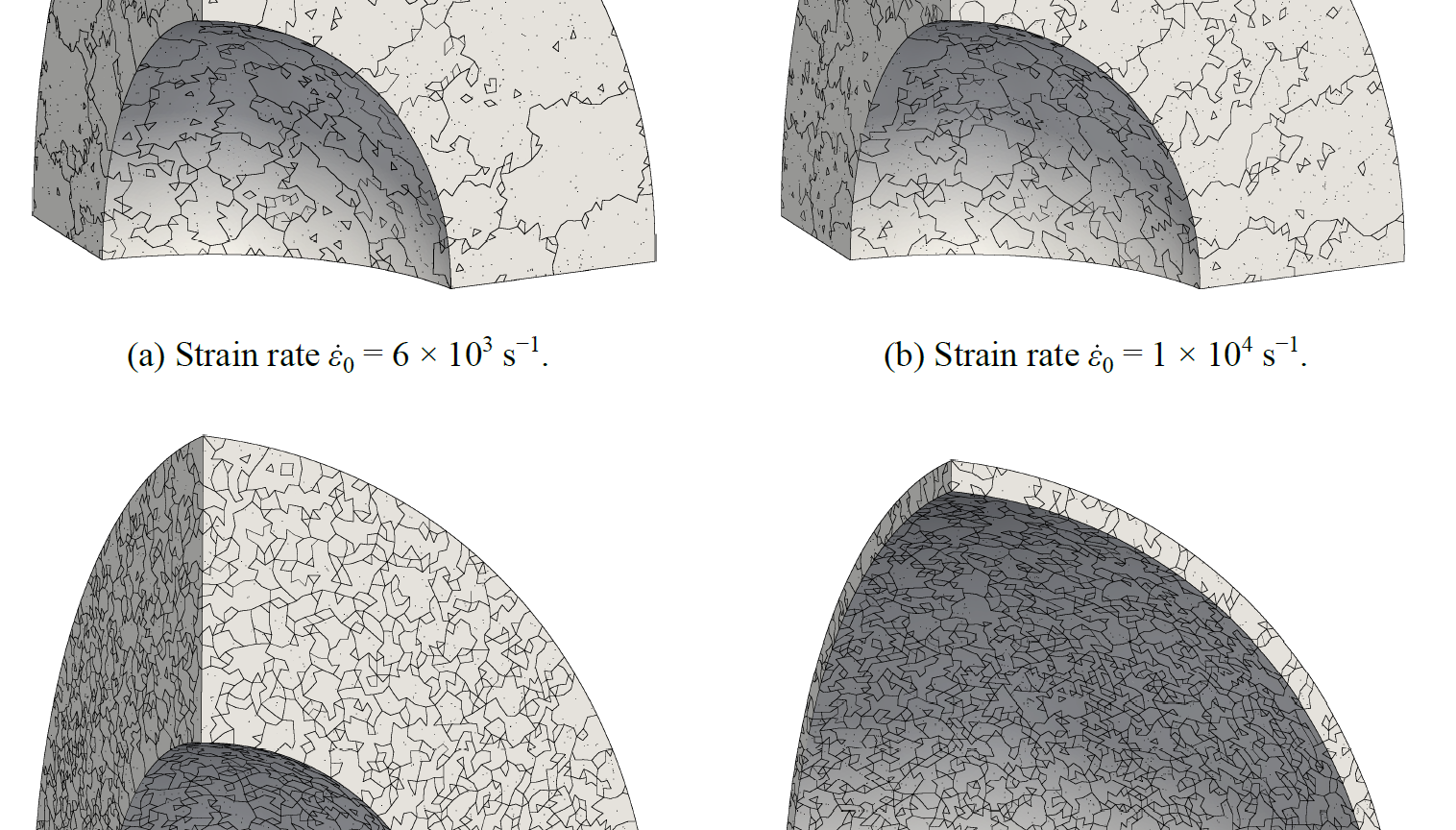
Figure: Dome subjected to radial expansion: borders of the fragments for different strain rates.