The research activities in the Chair focuses on the development, analysis and application of high-order accurate computational methods for time-dependent partial differential equations with a particular emphasis on linear and nonlinear wave problems. This has and continues to included research activities in discontinuous Galerkin and spectral methods, certificed reduced basis methods, methods for uncertainty quantification, methods for multiscale problems in time and space, efficient multilevel solvers and fractional differential equations. A major recent activity is the use of machine learning techniques in computational science with an emphasis on methods that preserve physical characteristics or the use of local neural networks to accelerate existing methods rather than replacing them.
While the emphasis in on the development and analysis of new methods and algorithms, the research is application driven and we generally maintain a strong focus on tying the theoretical developments to real applications, ranging from electromagnetics and plasma physics to geoscience and combustion. There is also a sustained interest in the development of methods and algorithms for parallel computing, GPU accelerated computing and the development of resilient algorithms, to support the development and use of large scale computational tool to enable predictive similation science.
 Spectral and Discontinuous Galerkin methods and applications All aspects of high-order, spectral and discontinuous Galerkin methods and their application are being considered. The emphasis is on nodal techniques and approached that enable efficient and accurate implementations on large scale computational platforms. Activities include efficient solvers and preconditioning, efficient time-stepping methods, and limiting in problems with shocks. Applications has included water waves, electromagnetics, plasma physics, and geophysics.
Spectral and Discontinuous Galerkin methods and applications All aspects of high-order, spectral and discontinuous Galerkin methods and their application are being considered. The emphasis is on nodal techniques and approached that enable efficient and accurate implementations on large scale computational platforms. Activities include efficient solvers and preconditioning, efficient time-stepping methods, and limiting in problems with shocks. Applications has included water waves, electromagnetics, plasma physics, and geophysics.
 Certified reduced basis methods While computational techniques continue to improve, the challenges associated with the rapid solution of parameterized partial differential equations remains a major computational bottleneck. However, such techniques are essential for the practical solution of many types of problems found in optimization, design, and real time control. We focus on techniques for which a rigorous and tight error can be computed during the online computation, resulting in a certified reduced basis methods. Recent efforts involve the combination of reduced basis methods with techniques from machine learning to accelerate reduced basis methods for nonlinear and/or time-dependent problems.
Certified reduced basis methods While computational techniques continue to improve, the challenges associated with the rapid solution of parameterized partial differential equations remains a major computational bottleneck. However, such techniques are essential for the practical solution of many types of problems found in optimization, design, and real time control. We focus on techniques for which a rigorous and tight error can be computed during the online computation, resulting in a certified reduced basis methods. Recent efforts involve the combination of reduced basis methods with techniques from machine learning to accelerate reduced basis methods for nonlinear and/or time-dependent problems.
 Precision algorithms through machine learning Many algorithms have nonlinear elements or parameters that need to be set to optimise the overall performance. However, this is known to be difficult to do across different applications. Furthermore, many methods have computational bottlenecks in which a majority of the computational effort is spend. We explore the use of machine learning techniques to replace such elements in existing algorithms to secure improved performance, ie rather than seeking to replace existing techniques we explore the use of machine learning techniques in a collaborative fashion. This also involves the development of machine learning techniques which respect physical constraints.
Precision algorithms through machine learning Many algorithms have nonlinear elements or parameters that need to be set to optimise the overall performance. However, this is known to be difficult to do across different applications. Furthermore, many methods have computational bottlenecks in which a majority of the computational effort is spend. We explore the use of machine learning techniques to replace such elements in existing algorithms to secure improved performance, ie rather than seeking to replace existing techniques we explore the use of machine learning techniques in a collaborative fashion. This also involves the development of machine learning techniques which respect physical constraints.
 Fractional differential equations The extention of classic calculus to fractional orders is an essential tool in the description of a variety of problems, eg problems with memory or, more generally, problems exhibiting non-Markovian behavior. We develop and analyse high-order accurate spectral and discontinuous Galerkin methods for the solution of fractional differential and partial differential equations with an emphasis on accuracy and efficiency of the methods.
Fractional differential equations The extention of classic calculus to fractional orders is an essential tool in the description of a variety of problems, eg problems with memory or, more generally, problems exhibiting non-Markovian behavior. We develop and analyse high-order accurate spectral and discontinuous Galerkin methods for the solution of fractional differential and partial differential equations with an emphasis on accuracy and efficiency of the methods.
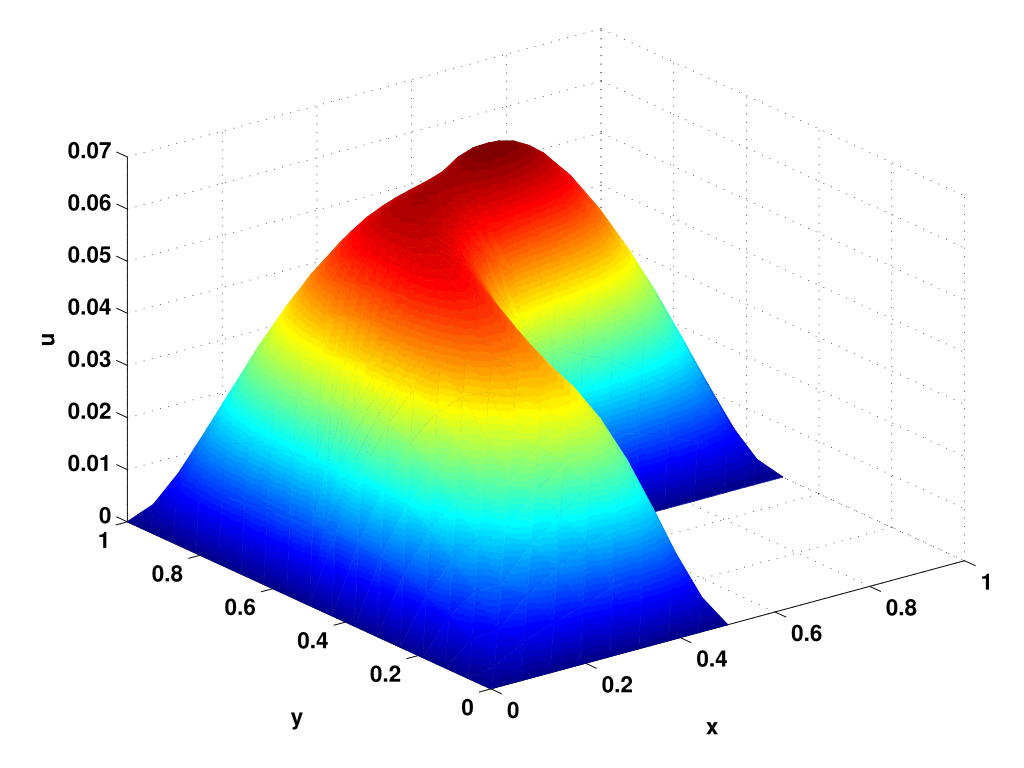 Multiscale methods in space and time Computational modeling of problems exhibiting multiscale behvaior is challenged by the need to accurately resolve the finest scales of the problem, often rendering the direct modeling infeasible, We study a variety of computational and analytic techniques to overcome this bottleneck, including numerical homogenization, multi-scale finite element methods, and integration methods for very stiff differential equations. Applications include sound propagation in the human lung, material modeling and multi-scale techniques in plasma turbulence.
Multiscale methods in space and time Computational modeling of problems exhibiting multiscale behvaior is challenged by the need to accurately resolve the finest scales of the problem, often rendering the direct modeling infeasible, We study a variety of computational and analytic techniques to overcome this bottleneck, including numerical homogenization, multi-scale finite element methods, and integration methods for very stiff differential equations. Applications include sound propagation in the human lung, material modeling and multi-scale techniques in plasma turbulence.
 High-dimensional problems and uncertainty quantification As computational techniques for solving deterministic problems mature, the uncertainty and randomness associated with large scale realistic problems present limits to how accurate such problems can be solved. We focus on the development of efficient computational techniques to deal with such situations, often leading high-dimensional parametrized problems. We consider chaos expansions, AVOVA based techniques for parameter compression, reduced models for efficient sampling, and other methods from statistics and probability. Applications are drawn from electromagnetic scattering, EMC/EMI problems and structural health monitoring.
High-dimensional problems and uncertainty quantification As computational techniques for solving deterministic problems mature, the uncertainty and randomness associated with large scale realistic problems present limits to how accurate such problems can be solved. We focus on the development of efficient computational techniques to deal with such situations, often leading high-dimensional parametrized problems. We consider chaos expansions, AVOVA based techniques for parameter compression, reduced models for efficient sampling, and other methods from statistics and probability. Applications are drawn from electromagnetic scattering, EMC/EMI problems and structural health monitoring.
 Computational electromagnetics and plasma physics High-order accurate and discontinuous Galerkin methods continue are being pursue to enable the accurate and efficient solution of large scale wave dominated problems in time-domain electromagnetics and kinetic plasma physics. The emphasis is on maturing such techniques to enable to the solution of large scale geometrically complex applications with a strong interaction between geometries, materials, fields and particles.
Computational electromagnetics and plasma physics High-order accurate and discontinuous Galerkin methods continue are being pursue to enable the accurate and efficient solution of large scale wave dominated problems in time-domain electromagnetics and kinetic plasma physics. The emphasis is on maturing such techniques to enable to the solution of large scale geometrically complex applications with a strong interaction between geometries, materials, fields and particles.
 Geophysical flows Many geophysical flows are characterized by being highly complex multi-physics, multi-scale phenomena, requiring the use of advanced computational techniques to enable the accurate modeling of such problems.We develop and analysis of high-order adaptive accurate methods for problems including magma flow in the mantel, the formation of volcanos and global models for tsunami predictions.
Geophysical flows Many geophysical flows are characterized by being highly complex multi-physics, multi-scale phenomena, requiring the use of advanced computational techniques to enable the accurate modeling of such problems.We develop and analysis of high-order adaptive accurate methods for problems including magma flow in the mantel, the formation of volcanos and global models for tsunami predictions.
 High-performance and GPU accelerated computing For many of the application being considered, the use of high-performance computing is a necessity, including the development of robust software for parallel computing environments. A recent development is the use of Graphics Processing Units (GPU’s) with the potential to truly transform the types of problems we consider and the algorithmic choices most suitable for such highly parallel architectures. Impressive accelerations have been demonstrated by using GPU’s, in particular for high-order accurate methods where the high arithmetic density is well suited for GPU’s.
High-performance and GPU accelerated computing For many of the application being considered, the use of high-performance computing is a necessity, including the development of robust software for parallel computing environments. A recent development is the use of Graphics Processing Units (GPU’s) with the potential to truly transform the types of problems we consider and the algorithmic choices most suitable for such highly parallel architectures. Impressive accelerations have been demonstrated by using GPU’s, in particular for high-order accurate methods where the high arithmetic density is well suited for GPU’s.