Humans and animals learn even in the absence of rewards: e.g., tourists like to explore a new city and children like to explore a new toy. What is the drive for doing this and what is happening in the brain during reward-free learning?
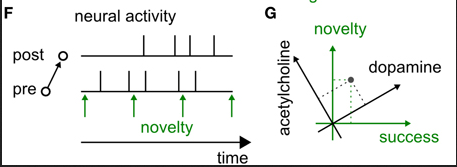
In the neurosciences, the process of learning corresponds to changes in the strength of a connection (or synapse) between two neurons. The classic paradigm is that of Hebbian learning: the changes of a connection from neuron A to neuron B depend on the state (e.g., the activity ) of those two neurons but not on that of other neurons that are far away. Thus Hebbian learning rules involve only two LOCAL factors: presynaptic activity and the state of the postsynaptic neuron. We explore generalizations of Hebbian learning that involve in addition to the two local ones or several other factors. In particular, we focus on the role of the broadcast signals of neuromodulators that reach vast areas of the brain simultaneously.
The effect of neuromodulators is fairly well understood in reward-based learning (Schultz et al. 1997): the learning rate is boosted at moments when a reward is received that is larger than the expected reward. This boost is mainly signaled by the neuromodulator dopamine that broadcasts reward-related information to large brain areas. The plasticity rules of reward-based learning can be written as Hebbian plasticity modulated by a third factor, an example of neoHebbian three-factor rules.
Similarly, we hypothesize that surprising events boost the learning rate – even in experimental paradigms that are completely reward-free. We explore learning paradigms that contain sudden changes of the environments and plasticity rules that can be formulated as neoHebbian multi-factor learning rules. A few questions naturally arising in this context are: What is a suitable definition of surprise? How can we control surprise in psychophysical experiments? How can we separate surprise from reward? How can we formulate spiking neural networks that learn in a reward-free environment?
If we apply the terminology of machine learning, the paradigms we explore are those of unsupervised or self-supervised learning. In contrast to machine learning, however, we only consider learning rules that can be formulated as neoHebbian multi-factor learning rules. In particular, in our view, the BackPropagation algorithm is not part of the tool box for biologically plausible candidate learning rules because it would involve neuron-specific error signals that need to be propagated by a separate and precisely tuned error-propagation network – and such precise error networks are unlikely to exist. In contrast to these, broadcast signals that are distributed to large populations of neurons are well established experimentally. We do not believe that these broadcast signals are neuron-specific (different for each neuron), but recent experiments show that they can vary from one brain area to the next or exhibit a gradient within an area.
Recent papers from the LCN
H.A. Xu, A. Modirshanechi, M.P. Lehmann, W. Gerstner, M.H. Herzog (2021)
Novelty is not Surprise: Human exploratory and adaptive behavior in sequential decision-making.
PLoS Comput Biol 17: e1009070.
V. Liakoni, A. Modirshanechi, W. Gerstner, and J. Brea (2021).
Learning in Volatile environments with the Bayes Factor Surprise
Neural Computation 33: 1-72
B. Illing, J. Ventura, G. Bellec, W. Gerstner(2020)
Local plasticity rules can learn deep representations using self-supervised contrastive predictions
Presented at NeurIPS workshop 2020.
M. Faraji, K. Preuschoff and W. Gerstner (2018)
Balancing New Against Old Information: The Role of Puzzlement Surprise in Learning.
Neural Computation 30: 34-83
W. Gerstner, M. Lehmann, V. Liakoni, and J. Brea (2018)
Eligibility traces and plasticity on behavioral time scales: experimental support of NeoHebbian three-factor learning rules.
Front. Neural Circuits, 12:53
N. Fremaux and W. Gerstner (2016)
Neuromodulated Spike-Timing-Dependent Plasticity, and Theory of Three-Factor Learning Rules
Front. Neural Circuits 9:85