Quantum measurements of mechanical oscillators (D. Wilson et al. Nature 2015, V. Sudhir PRX 2018, Sudhir et al. PRX 2018, A. Ghadimi, Science 2018)
The precision measurement of position is a long-standing tradition in physics. The 17th century experiments of Cavendish that established the inverse square law of gravitation using precise measurements of a torsion pendulum, the early 20th century experiments of Perrin that proved the atomic hypothesis by studying thermal (“Brownian”) motion of particulate matter, and the recent detection of gravitational waves by the Laser Interferometric Gravitational-wave Observatory (LIGO), all belong to this rich heritage. The research group of Kippenberg at EPFL has performed one of the most precise measurement of the quantum mechanical zero-point motion of a macroscopic mechanical oscillator [1,2]. This was achieved by a nearly 17 orders of magnitude improvement in displacement sensitivity over the last century (see Figure 1), of which, more than two orders of magnitude improvement was made by the Kippenberg laboratory.
This major advance has builds on a decade-long exploration of near-field cavity optomechanics: a platform for sensitive interferometric readout of nanomechanical motion. Realizing this sensitivity with a nano-object, however, requires confining the optical field to dimensions much smaller than a wavelength. The strategy of the Kippenberg laboratory involves guiding the optical field along the periphery of micron-thick glass disk by total internal reflection (a so-called whispering gallery mode microcavity). To couple the nanomechanical object to this field, it was integrated within 20 nm of the disk, sufficient to sample the field’s wavelength-scale evanescence [7]. The laboratory has developed a fabrication technique enables to integrate a nanomechanical object known to have exceptionally high-Q mechanical resonances with optical resonators (i.e. nano-optomechanical systems). Taking advantage of several unique properties of whispering gallery mode (WGM) microcavities, it was possible to perform a near ideal interferometric measurement of the string’s displacement. Taken together, these capabilities allowed to achieve an absolute interferometric displacement sensitivity of , a value that is four orders of magnitude smaller than the zero-point motion of the fundamental string mode [2]. At the time of its original reporting, a displacement measurement 40 dB below the vacuum fluctuations of a solid-state mechanical oscillator was unprecedented by three orders of magnitude. Remarkably, the strength of the measurement necessary to achieve this sensitivity implies that the violin mode of the nanostring must necessarily be driven, by radiation pressure shot noise, to an effective temperature of several Kelvin. In the reported measurements, the laboratory observed this long-sought-after signature of quantum measurement back-action, and verified that the product of the imprecision and the back-action is within a factor of 5 of the ideal limit set by the uncertainty principle [2].
A central question the Kippenberg laboratory has pursued has been how to measure the zero point motion of a engineered macroscopic mechanical oscillator. This can be achieved with optical interferometry, in which the position of a mirror is imprinted onto the phase of an optical field. Such measurements are intrinsically subject to Quantum Mechanics: the mirror’s position is also obscured by momentum transfer of photons (radiation pressure shot noise). The magnitude of these two sources of position noise are inversely proportional, so that total position noise has an absolute minimum which precisely corresponds to the zero-point motion of the mirror. Thus, any attempt to resolve the zero-point motion of the mirror necessarily obscure it. This fundamental radiation pressure quantum noise is an example of “quantum measurement back-action” and the minimum position measurement noise is known as the Standard Quantum Limit (SQL). The observation of quantum measurement back-action on a macroscopic mechanical object has been an open challenge for the optical interferometry community for over 30 years, tracing the development of LIGO. The Kippenberg laboratory, has carried out experiments that have observed, suppressed, or erased quantum backaction for the first time at room temperature [2,5,6] and made measurements with a record imprecision of more than 40dB below the SQL.
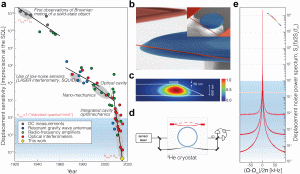
Building on this advance, the Kippenberg laboratory has since demonstrated techniques to suppress or evade quantum back-action [5,6]. One strategy is to use feedback, since the motion produced by back-action is written directly onto the measurement record. Using radiation pressure from an auxiliary laser field as the actuator, the laboratory has been able to feedback and suppress quantum back-action by three orders of magnitude. This experiment has been the first demonstration of quantum feedback of a mechanical oscillator. In doing so, the thermal motion of the string mode is simultaneously suppressed, reducing its effective temperature to 100 mK. At this temperature, the average phonon occupation of the string mode is 5, meaning that it spends over 15% of its time in its ground state. Efficient feedback cooling of this sort is a canonical example of “continuous quantum feedback” [8]. Remarkably, a phonon occupation of 5 is unprecedented for feedback cooling of both macroscopic and microscopic objects (such as trapped ions and neutral atoms). This surprising achievement is a consequence of the scarcity of Heisenberg-limited position measurements; optical interferometry is one of the few practical examples.
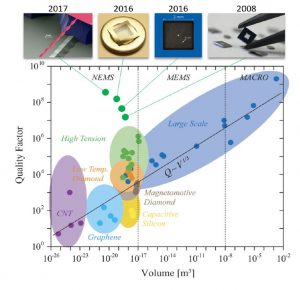
Feedback can be used to suppress measurement back-action, but not to evade the SQL. Towards this end, the laboratory has also demonstrated techniques to “erase” back-action from a displacement measurement [6], making use of the fact that the back-action and imprecision noise are correlated. These correlations – generated from a room-temperature nanomechanical oscillator – were used to coherently cancel quantum back-action, allowing to perform quantum-enhanced force metrology. Finally, the Kippenberg research laboratory has demonstrated the most coherent mechanical oscillators to date [9], via strain engineering: Specifically, by micropatterning thin films of highly strained silicon nitride string and membrane-like nanoresonators with room temperature quality factors in excess of 900 million have been realized [7]. This constitutes the highest room temperature mechanical Q factor of any mechanical oscillator, irrespective of shape, mass or frequency. The same string can exhibit hundreds of oscillations in its thermal decoherence time, ms, approaching the performance of single trapped ions. Coupled to optical cavities, this new class of ultra-coherent nanomechanical resonators has the potential to usher in a new era of room temperature quantum optomechanics, with applications ranging from sources of squeezed light, quantum-enhanced force sensing, and self-calibrated quantum noise thermometry, to hybrid quantum systems.
References:
[1] V. Sudhir, Quantum Limits on Measurement and Control of a Mechanical Oscillator (Springer, 2017).
[2] D. J. Wilson, V. Sudhir, N. Piro, R. Schilling, A. Ghadimi, and T. J. Kippenberg, Nature 524, 325 (2015).
[3] V. B. Braginsky and Y. I. Vorontsov, Sov. Phys. Uspekhi 17, 644 (1975).
[4] C. Caves, Phys. Rev. Lett. 45, 75 (1980).
[5] V. Sudhir, D. J. Wilson, R. Schilling, H. Schütz, S. A. Fedorov, A. H. Ghadimi, A. Nunnenkamp, and T. J. Kippenberg, Phys. Rev. X 7, 011001 (2017).
[6] V. Sudhir, R. Schilling, S. A. Fedorov, H. Schütz, D. J. Wilson, and T. J. Kippenberg, Phys. Rev. X 7, 031055 (2017).
[7] R. Schilling, H. Schütz, A. H. Ghadimi, V. Sudhir, D. J. Wilson, and T. J. Kippenberg, Phys. Rev. Appl. 5, 054019 (2016).
[8] H. Wiseman, Phys. Rev. A 51, 2459 (1995).
[9] A. Ghadimi et al. Science (2018)