One of the motivational challenges in the field of cavity optomechanics has been the realization of a true macroscopic system which exhibits quantum mechanical behaviour. Following the precedent set in the atomic physics community, the goal has been to first achieve what is usually termed strong coupling [1] – a necessary step en route to full quantum control.
In our group, we have pioneered the use of a microfabricated high-finesse toroidal optical cavity, coupled to its own mechanical radial breathing mode, as shown in Figure 1. Such devices, when operated at cryogenic temperatures, around 500 mK in our group, have their mechanical motion passively refrigerated to about 200 thermal phonons.
However, to observe persistent quantum coherence, such a thermal population is undesirable – the fundamental quantum fluctuations of the mechanical oscillator needs to equal or exceed its thermal fluctuations. Inspired by techniques developed in atomic physics [2], we combat the thermal population by laser cooling the mechanical mode. This process harnesses the low-entropy character of the laser photons that circulate in the optical cavity, to swap out the high-entropy thermal phonons. We have employed this laser cooling technique to place the mechanical oscillator in its ground state 37% of the time [3].
It turns out that the ability to laser cool to near the ground state does not translate to the ability to preserve quantum coherence; the latter has a much more stringent requirement. In fact, in this regime one requires that the interaction between the optical photon and the mechanical phonon is stronger than the interaction of each of these subsystems with their respective thermal baths. This, so-called quantum coherent coupling regime, was demonstrated for the first time in the optical domain our group [3]. A typical signature of such a dominant coherent interaction is the hybridization of both the interacting subsystems, as evidenced in our experiment (Figure 2).

Figure1: A silica micro-toroid, supporting a high-finesse optical mode, and a high-Q mechanical radial breathing mode.
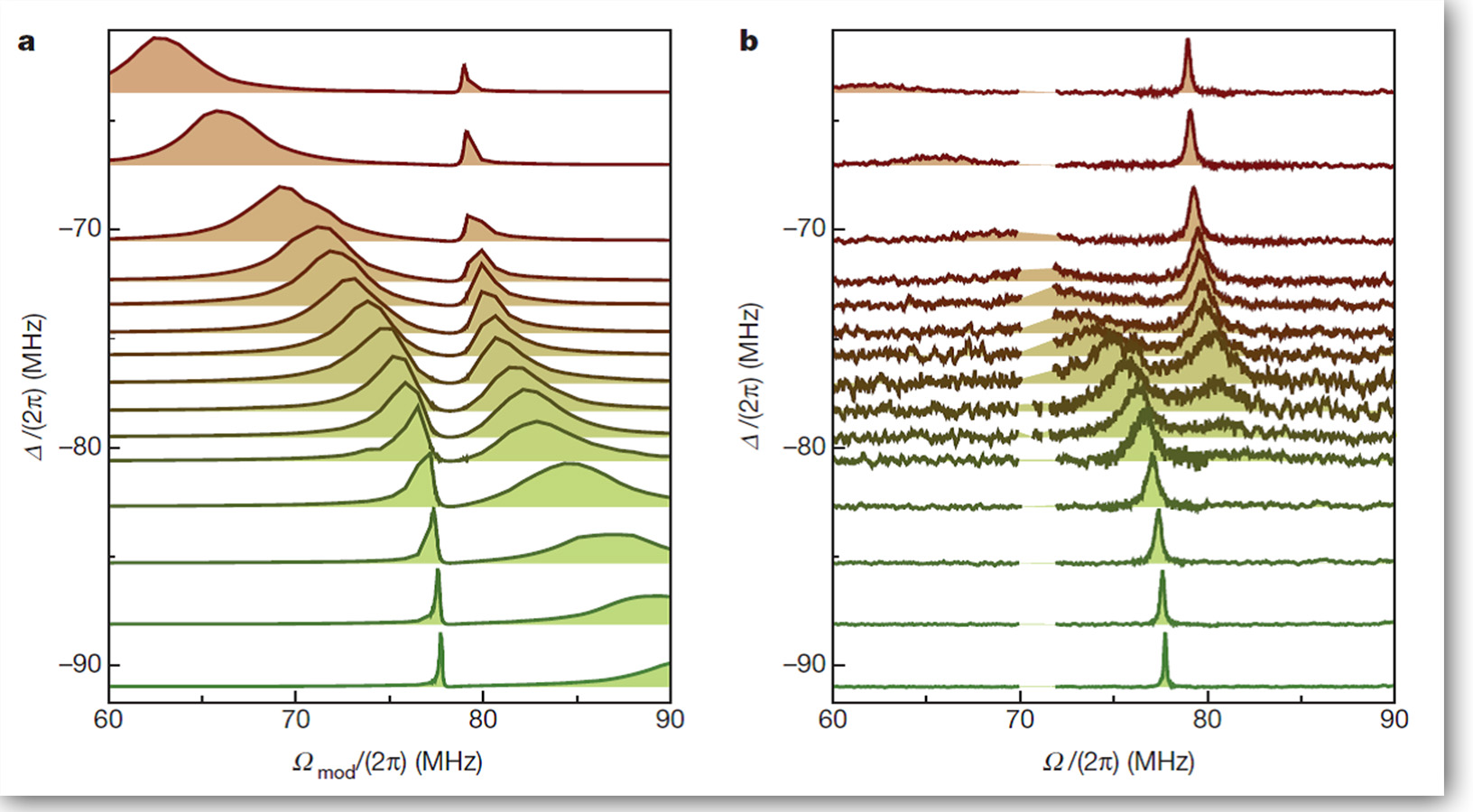
Figure 2: Normal-mode splitting observed in both the optical mode and the mechanical mode when they are in the quantum coherent coupling regime.
References
[1] H. J. Kimble, Phys. Scr. T76, 127 (1998).
[2] D. J. Wineland and W. M. Itano, Phys. Rev. A 20, 1520 (1979).
[3] E. Verhagen, S. Deleglise, S. Weis, A. Schliesser, and T. J. Kippenberg, Nature 482, 63 (2012).