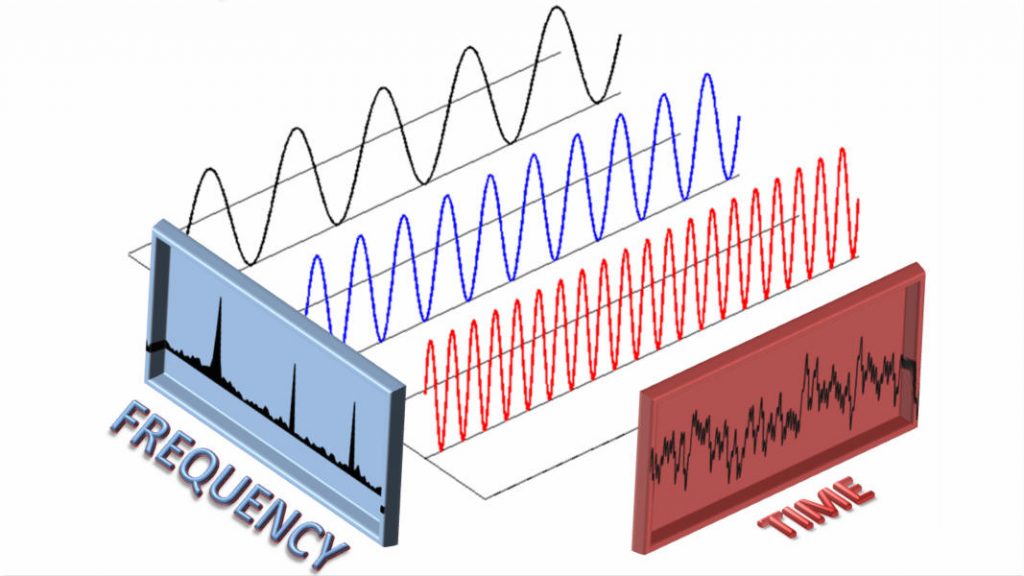
Prof. Hassanieh developed the Sparse Fourier Transform, a family of sublinear time algorithms for computing the Fourier transform faster than FFT by exploiting the inherent sparsity in real-world signals. The algorithms encompass two main axes: (1) Runtime Complexity: Sparse Fourier Transform algorithms that are faster than FFT and have the lowest runtime complexity known to date. (2) Sampling Complexity: Sparse Fourier Transform algorithms with optimal sampling complexity in the average case and the same nearly optimal runtime complexity. These algorithms use the minimum number of input samples and hence, reduce acquisition cost and I/O overhead. I also built systems that leverage these algorithms to address practical problems in five different research domains:
- GPS power consumption in mobile systems.
- Light-field photography in computer graphics.
- MRS (magnetic resonance spectroscopy) in medical imaging.
- NMR (nuclear magnetic resonance) in biochemistry.
- FFT chip design in digital circuits.
This work received the TR10 Award for the top ten breakthrough technologies and ACM Doctoral Dissertation Award.