Current interests
The following are examples of questions we are interested in currently:
- How do genetic and neuronal circuits solve conflicts between speed and resilience?
- What are the quantitative patterns of ‘system failure’ in biology?
- What are the consequences of fragility in biological systems?
- What are the quantitative laws of decision-making?
Our research moves fast and our interests change quickly. So, see our pre-prints and publications page for a list of our most recent completed projects.
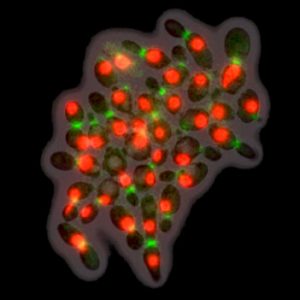
Postdoctoral research
As an independent Fellow at The Rockefeller University, I made a transition from theoretical physics to the intersection of biology and physics. Using theory and experiments, we answered the following questions:
In budding yeast, we found that two key parts of the cell cycle, periodic phosphorylation-degradation and transcription, are both under the control of the same CDK-APC/C oscillator. This result had been the subject of controversy previously. The number of oscillators makes a difference for establishing synchrony in wild-type cycles, for checkpoint arrest, and for artificially induced cell cycle arrest. We also found that a few genes constitute exceptions to this rule; they oscillate when the CDK-APC/C oscillator is blocked. Based on a mathematical analysis, we showed experimentally that one of these genes (SIC1) helps cell cycles with low mitotic cyclin-CDK levels, which is counter-intuitive because Sic1 is an inhibitor of mitotic cyclins. (Published.)
Biology emerges from interactions between molecules, which are challenging to elucidate with current techniques. An orthogonal approach is to probe for “response signatures” that identify specific circuit motifs, which describe interactions globally. For example, bistability, hysteresis, or irreversibility are used to detect positive feedback loops. For adapting systems, which are ubiquitous in biology, such signatures were not known. Two different circuit motifs generate adaptation: negative feedback loops (NFLs) and incoherent feedforward loops (IFFLs), which specify different interactions and exhibit different biology. Based on exhaustive computational testing and mathematical proofs, we proposed the first differential signatures: In response to oscillatory stimulation, NFLs but not IFFLs generically show i) ‘refractory period stabilization’ (robustness to changes in stimulus duration) or ii) ‘period skipping’. Applying this approach to wild-type and mutant yeast, including a synthetic IFFL circuit, we identified the circuit dominating cell cycle timing. In C. elegans AWA olfactory sensory neurons, which are crucial for chemotaxis, we uncovered a Calcium-NFL leading to adaptation, difficult to find by other means, especially in wild-type, intact animals. These response signatures allow direct access to the outlines of the wiring diagrams of adapting systems. (Published.)
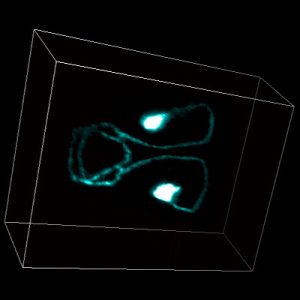
Graduate & undergraduate research
The focus of my graduate research was on quantum fluctuation forces, also known as Casimir forces. To calculate these forces, we developed an approach in which the geometric and material properties of the objects are represented by their electromagnetic scattering matrices. In addition to deriving an analytical closed-form expression for the force and investigating it in a variety of new geometries, we derived a theorem, which showed that quantum fluctuation forces cannot create stable configurations in vacuum.
In college and early graduate school, I worked in biophysics and computational biology, in particular, on solvation energies, protein surface maps, force-induced DNA melting, and protein-DNA recognition.