
Ulambator is a software tool that is developed at LFMI, which is dedicated to two-phase flows in microfluidic channels. The acronym Ulambator stands for Unsteady Laminar Microfluidic BEM Algorithm To Obtain Results [1].
An open-source version of the solver is available here. Currently further functionalities are being included and a documentation and preconfigured test cases will be complemented.
For academic institutions we offer workshops that teach the fundamental principles and user guidlines. Past workshops and course material is listed under Workshops.
If you have a question or encounter a problem don’t hesitate to write me: [email protected]
The numerical algorithm is based on the Boundary Element Method, which does not require a domain discretization but a boundary mesh only. Within the framework of the classical BEM no inertial terms can be accommodated and therefore the U for Unsteady highlights the deformability of the fluid interface and Laminar highlights flow at Reynolds number equal zero.
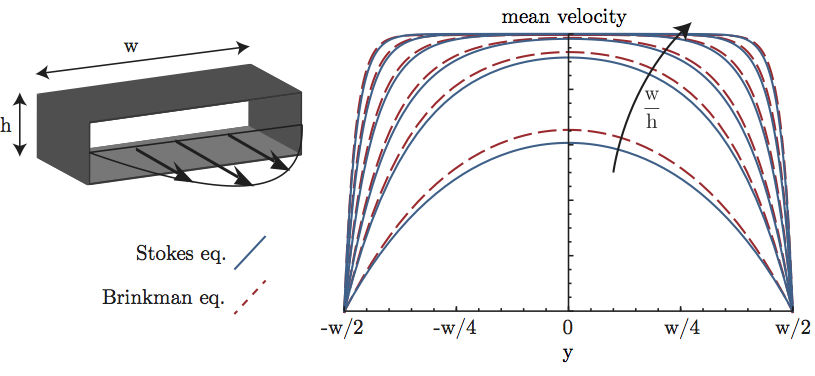
The solved flow equations are averaged over the height, leading to 2D equation, so called Brinkman equation, but necessitating in return channels of high aspect ratio, being much wider than high [2].
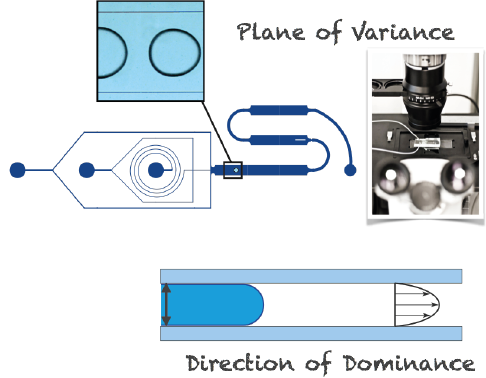
Adopting the point of view of the microscope operator the channel appears as a two dimensional slice, a depth averaged flow-field and the projection of the droplets fluid-fluid interface are resolved. We call this perspective the Plane of Variance because the geometric features of the channel and the droplet interface vary mostly in this plane. Perpendicular to the Plane of Variance is the Direction of Dominance, where the viscous stresses and capillary effects are usually higher due to the confinement in channels of high aspect ratio. In the direction of dominance there is only little variation and we therefore model dominant effects of the Direction of Dominance into the 2D simulation.
The figure below shows a flow through a rectangular channel. The blue line is the 3D Stokes solution and the red line the 2D Brinkman solution. The aspect ratio, width over height w/h, increases step wise from w/h=1 to 2, 3, 5, 8 and 12. On observes that for high aspect ratios the agreement improves and that even for w/h=1 the discrepancy is not tremendous.
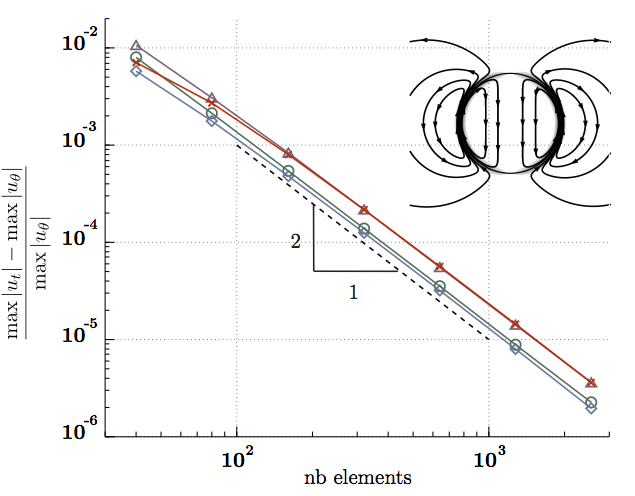
After this very brief illustration of the model we check the convergence of the numerical algorithm that uses piece-wise linear elements on the droplet interface. The graph below shows that the error decreases as the number of elements is increased. As one would expect the error decreases with inverse of the square of the number of elements. The solution that is calculated is that of a droplet under a gradient of the surface tension shown in the inset.
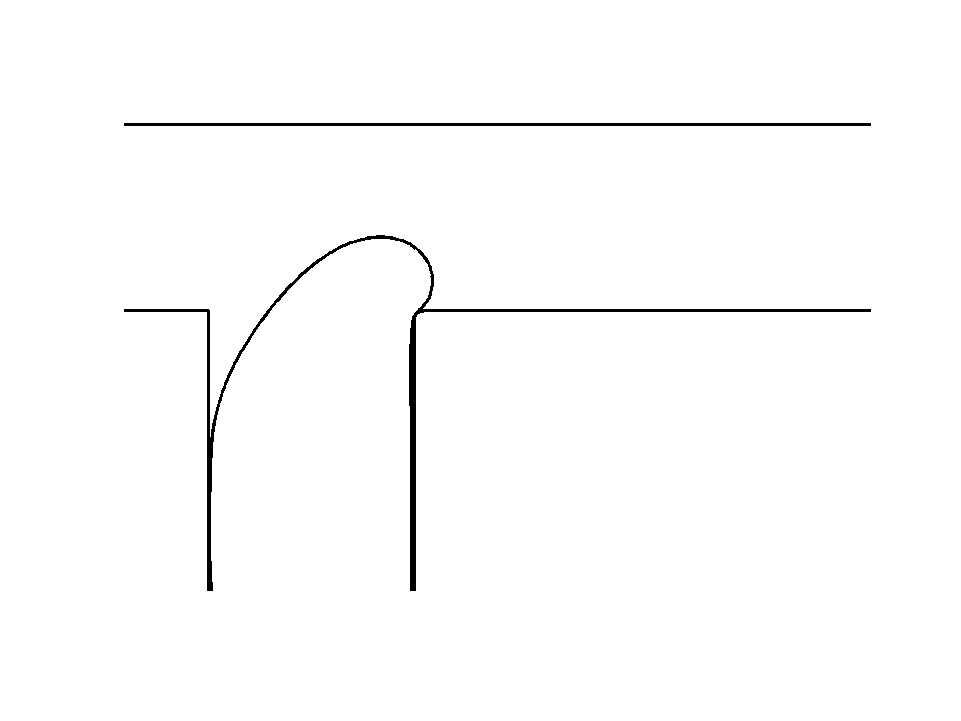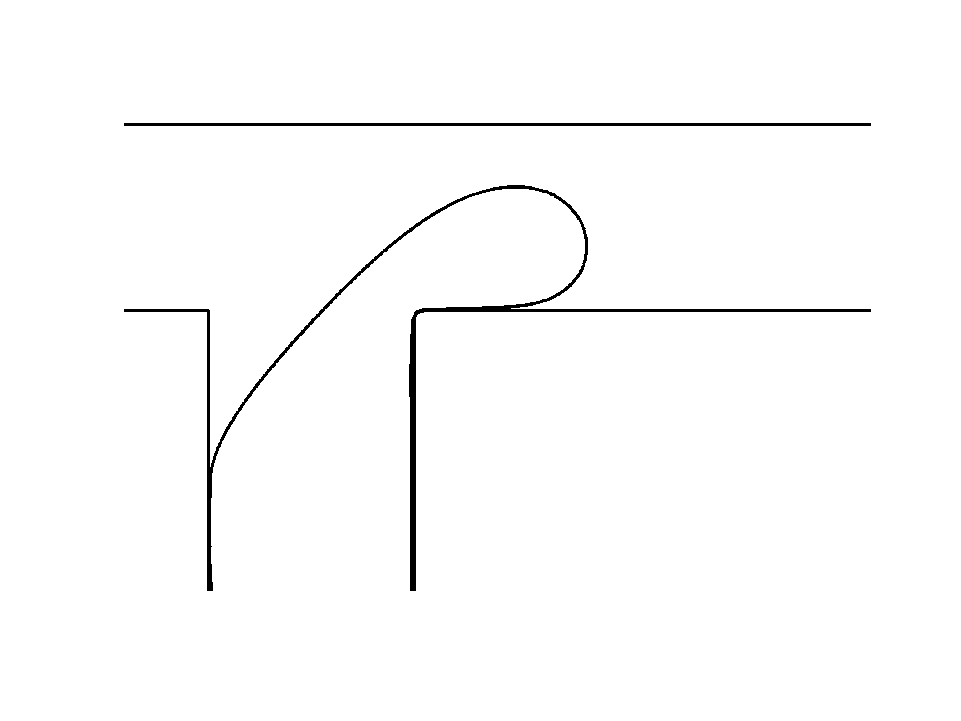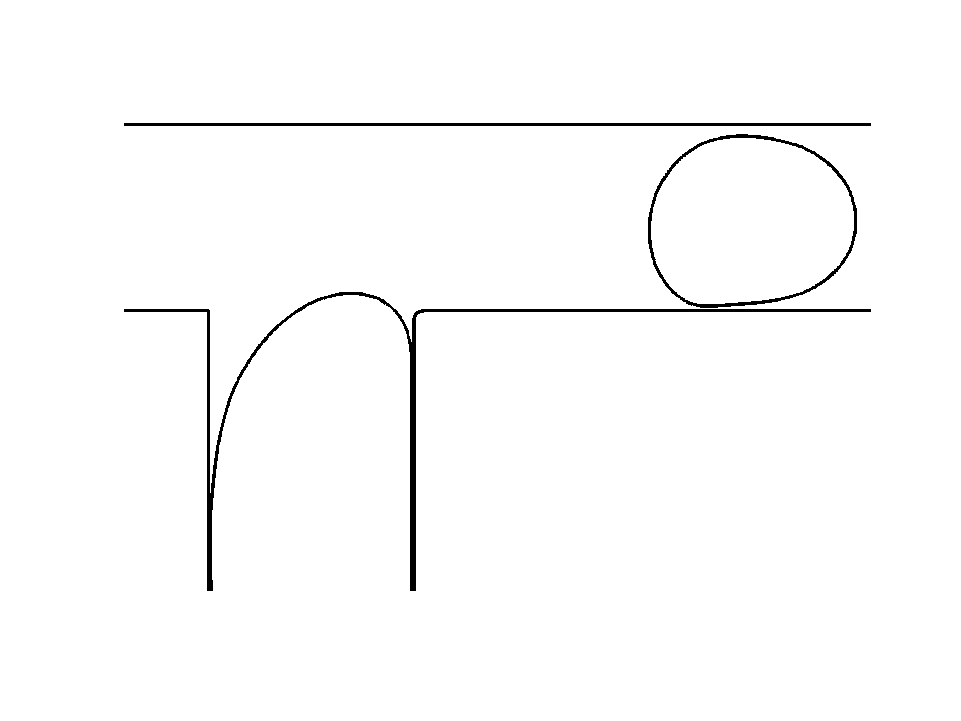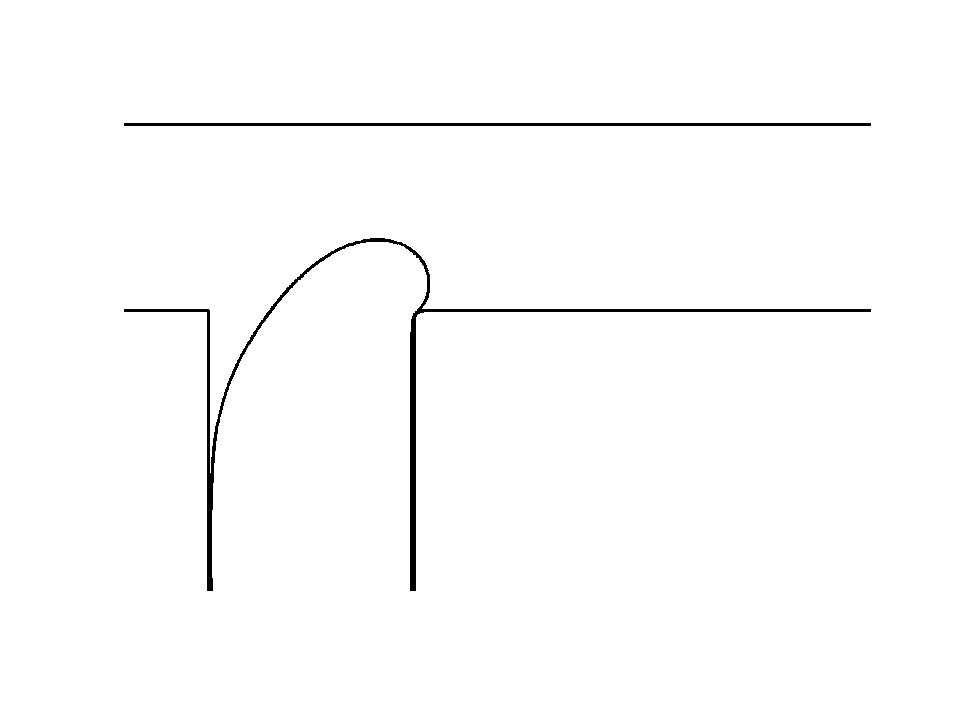
An important property to check is that a stable solution remains stable and unstable solution remain unstable in the numerical procedure. The analysis of flow stability is major research subject in our lab. We decided to simulate the Saffman-Taylor Instability and compare the growth of small sinusoidal perturbation to its theoretical prediction [3].
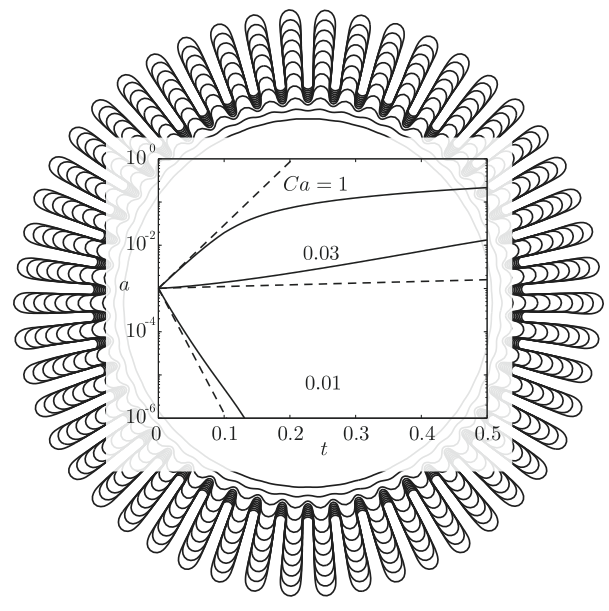
The Saffman-Taylor Instability, as illustrated in the background, forms fingers at a liquid-liquid interface, when a less viscous fluid is injected in a narrow gap between two glass plates and displaces a more viscous fluid. The graph shows the theoretical prediction for finger growth, conservation and decay. The simulation follows these predictions but differs after some time because the simulated problem evolves and is not represented by the initial theory anymore. The result shows that stable, neutral and unstable states are correctly captured.
A collection of animations illustrates the functionality of the Ulambator solver that incorporates robustness and versatility. Results that have been produced using Ulambator are shown in the Microfluidics section.
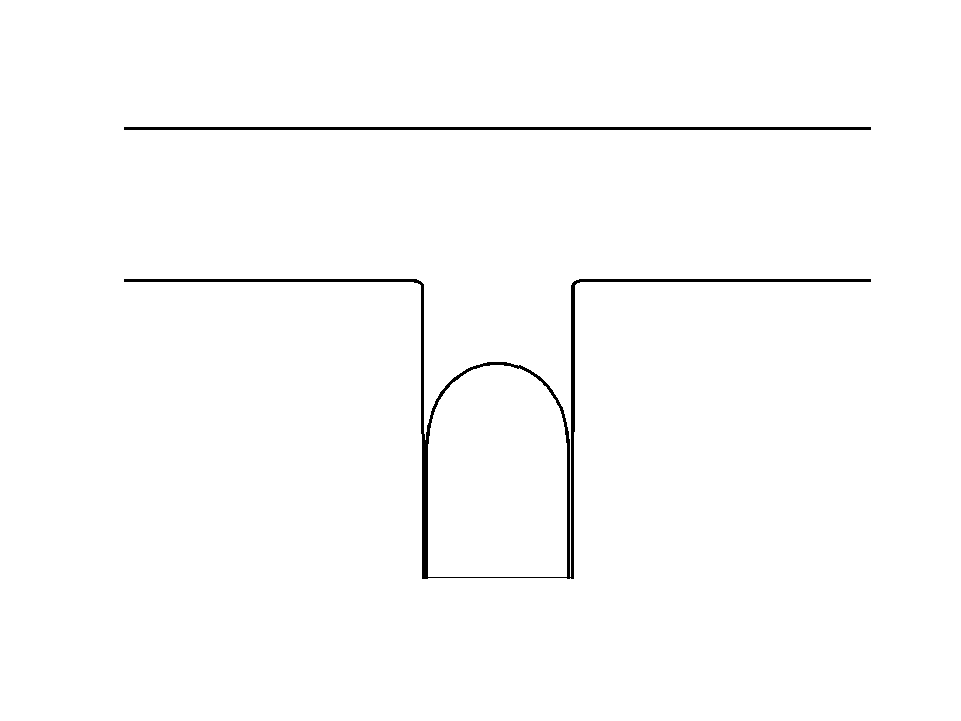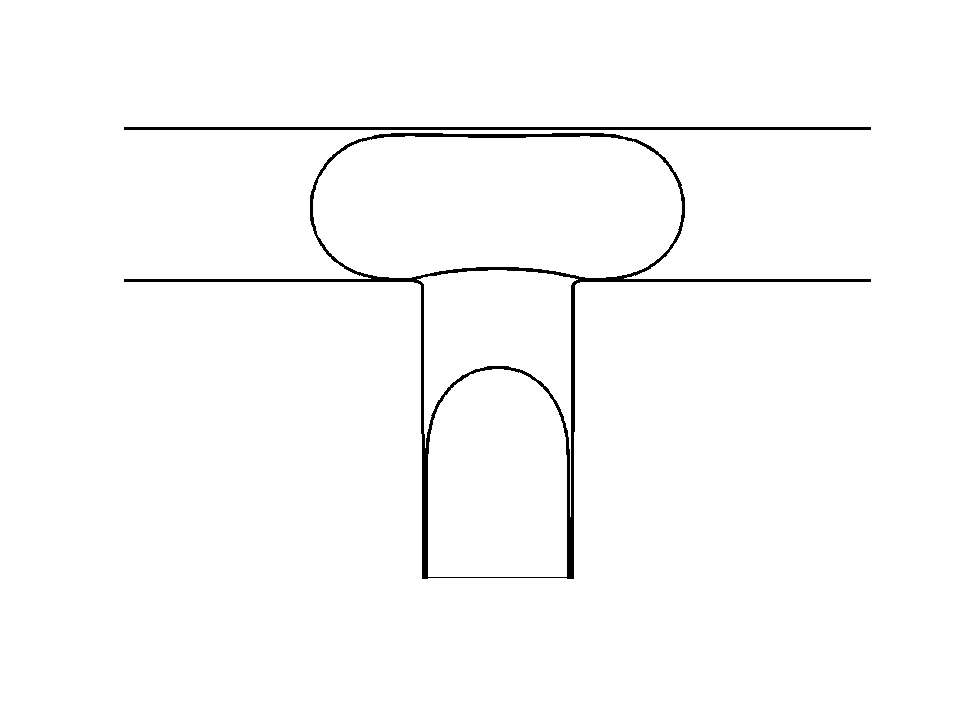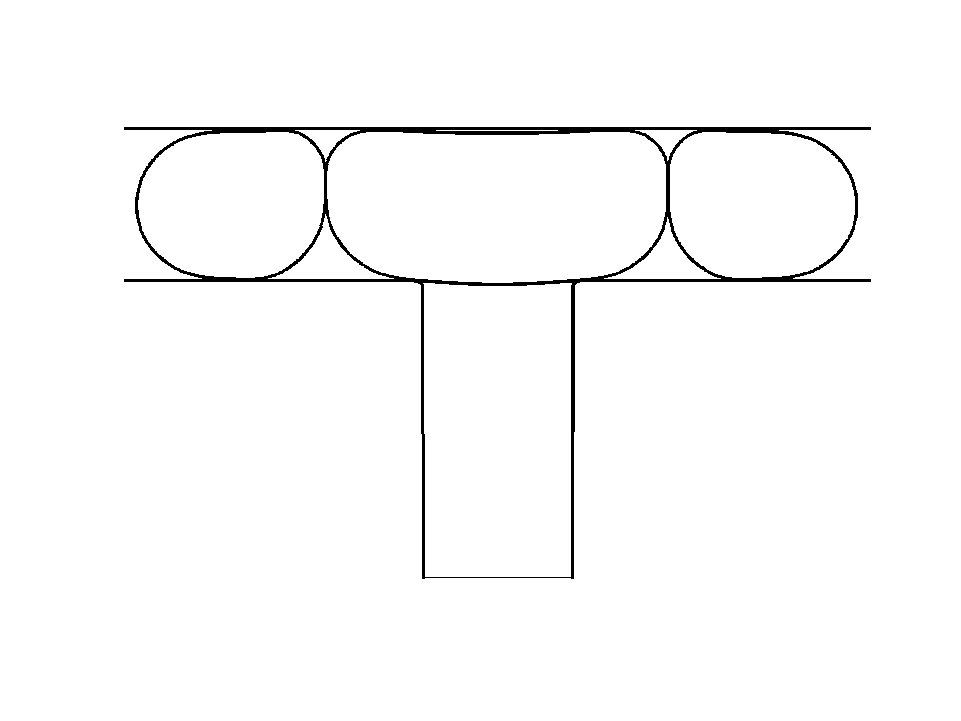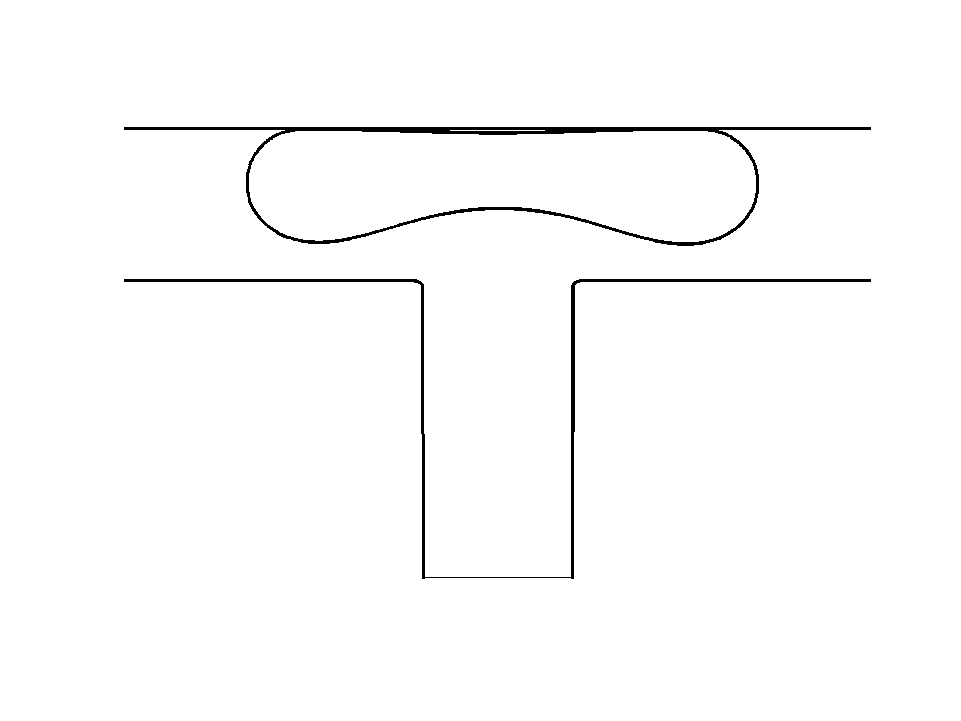
Droplet shedding at a T-junction1 Droplet with anchors2
Droplet shedding by flow focussing3 Droplet in mixing geometry4
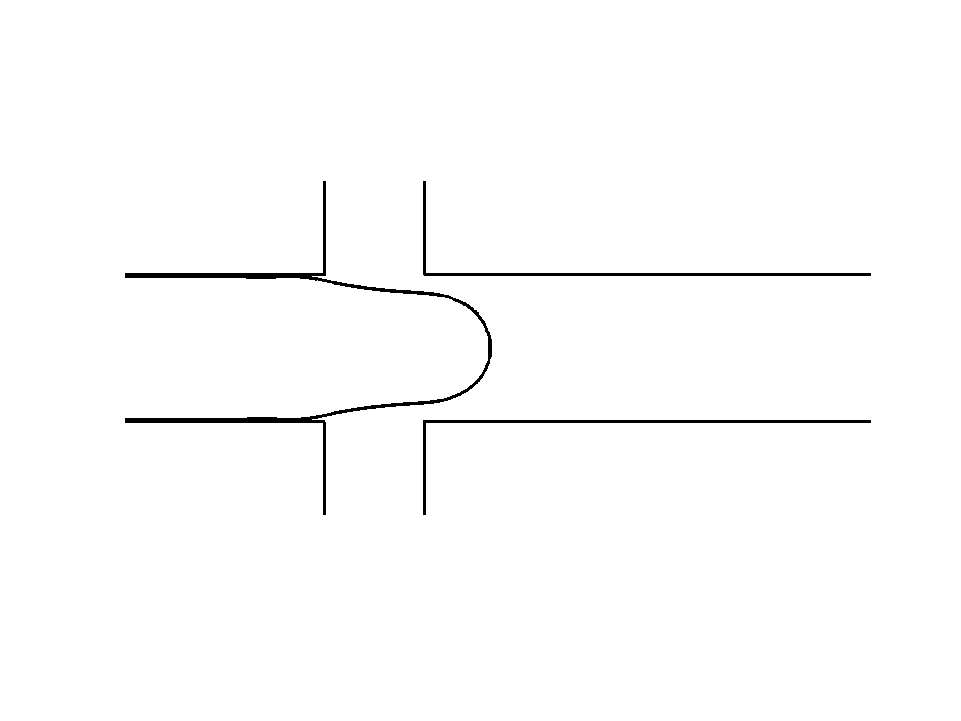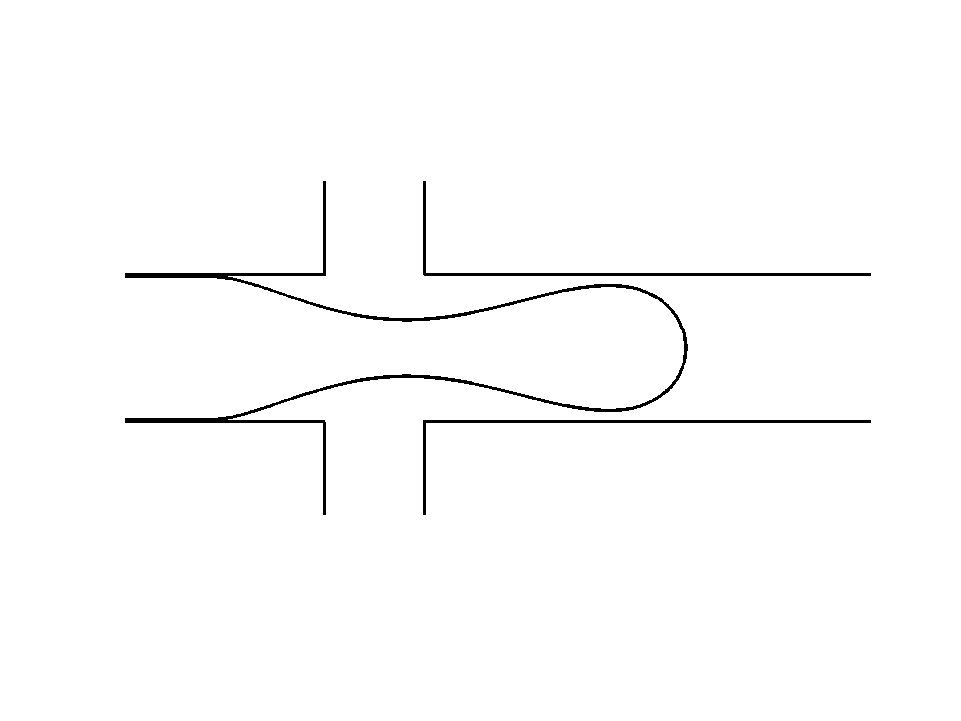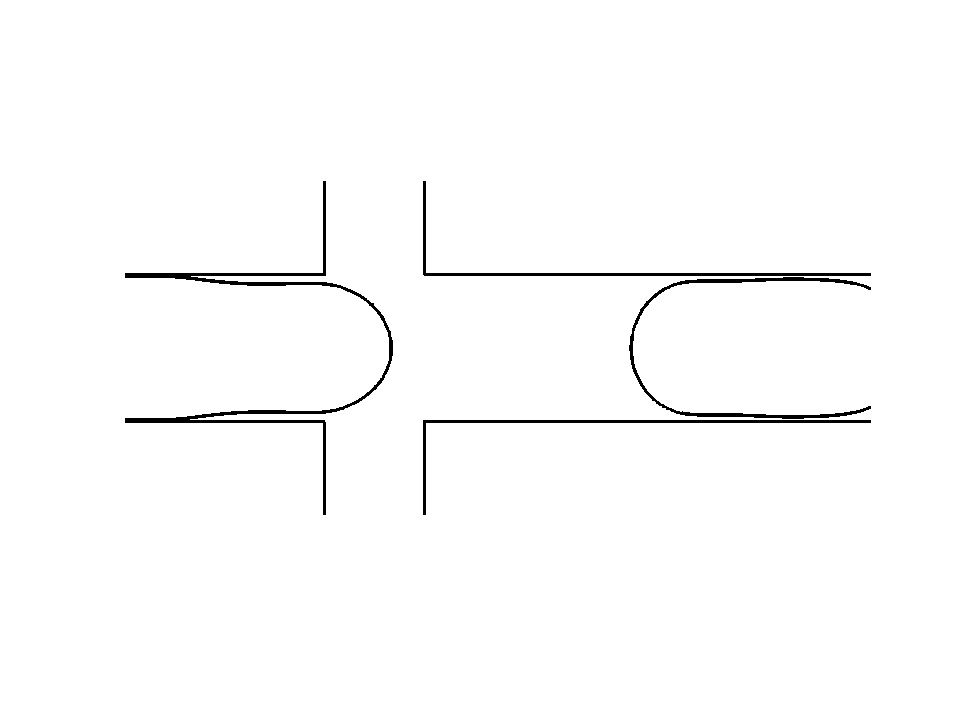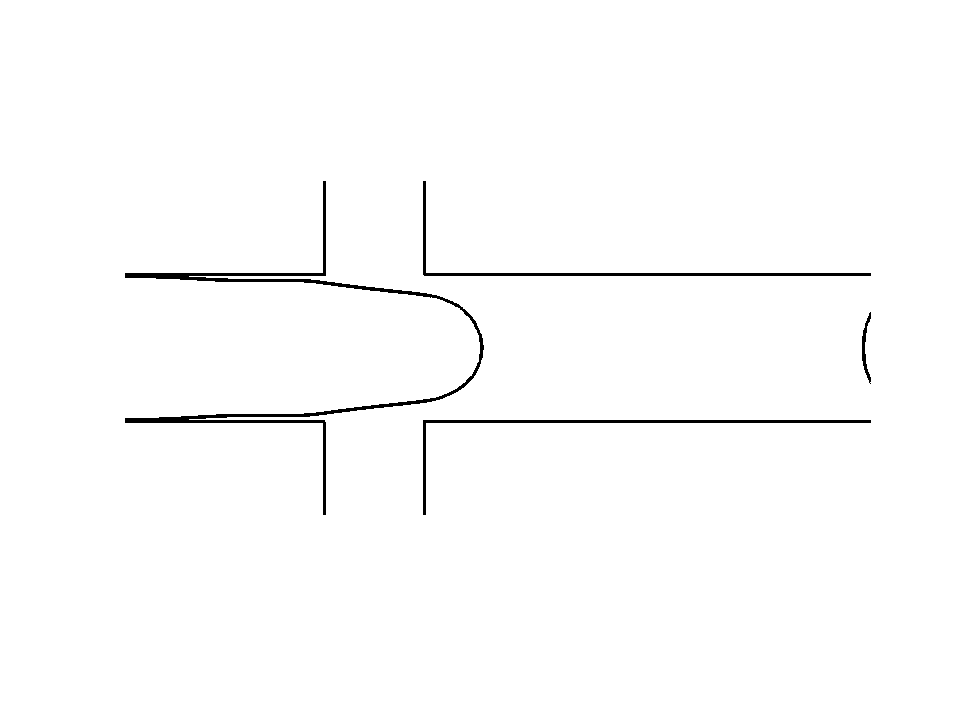

Droplet coalescence5 Droplet on droplet splitting6
This collection of animations was inspired by the website of Jean-Christophe Barets group.
http://dmi.ds.mpg.de/movies.php
1) Garstecki et al., “Formation of droplets and bubbles in a microfluidic T-junction: Scaling and mechanism of breakup,” Lab Chip 6, 437 (2006)
2) Dangla et al., “Rails and anchors: guiding and trapping droplet microreactors in two dimensions”, Lab Chip, 2011, 11
3) Garstecki et al., “Formation of monodisperse bubbles in a microfluidic flow-focusing device”, Applied Physics Letters, Vol. 85, No. 13
4) Bringer et al., “Microfluidic systems for chemical kinetics that rely on chaotic mixing in droplet”, Phil. Trans. R. Soc. Lond. A 362
5) Bremond et al., “Decompressing Emulsion Droplets Favors Coalescence”, PRL 100, 024501 (2008)
6) Jullien et al., “Droplet breakup in microfluidic T-junctions at small capillary numbers”, Phys. Fluids 21, 072001 (2009)
References:
[1] Boundary elements method for microfluidic two-phase flows in shallow channels, M. Nagel and F. Gallaire, Computers and Fluids, 107, pp 272-284 (2015), http://dx.doi.org/10.1016/j.compfluid.2014.10.016
[2] Marangoni induced force on a drop in a Hele-Shaw cell, F. Gallaire, P. Meliga, P. Laure and C. Baroud, Physics of Fluids, 26, pp 062105 (2014)
[3] A new prediction of wavelength selection in radial viscous fingering involving normal and tangential stresses, M. Nagel and F. Gallaire, Physics of Fluids, 25, 124107 (2013), http://dx.doi.org/10.1063/1.4849495