
Figure 1. (a) The separated vortex ri4ng downstream a flying dandelion seed. (b) The grid fins of the SpaceX Falcon 9-R.
The study of the behavior of wake flows past porous bodies is gaining more and more interest both in natural studies and engineering applications.
In nature, there are many examples of structures characterized by the presence of voids. The dandelion seeds are transported in the air by a parachute-like structure called pappus. The porous structure drastically decreases the falling velocity and stabilizes the steady flow at Reynolds Numbers in which a bulk disk is characterized by an unsteady wake pattern (figure 1(a)) [1,2].
Besides these natural examples, porous bodies are ubiquitous in industrial processes, as cooling and filtering systems, oil reservoirs, wastewater treatment systems, and the flow around porous bluff bodies, as parachutes and nets. The SpaceX Falcon 9-R presents grid fins that are being used for increased precision in control of the landing location for reusable launch vehicles (figure 1(b)).
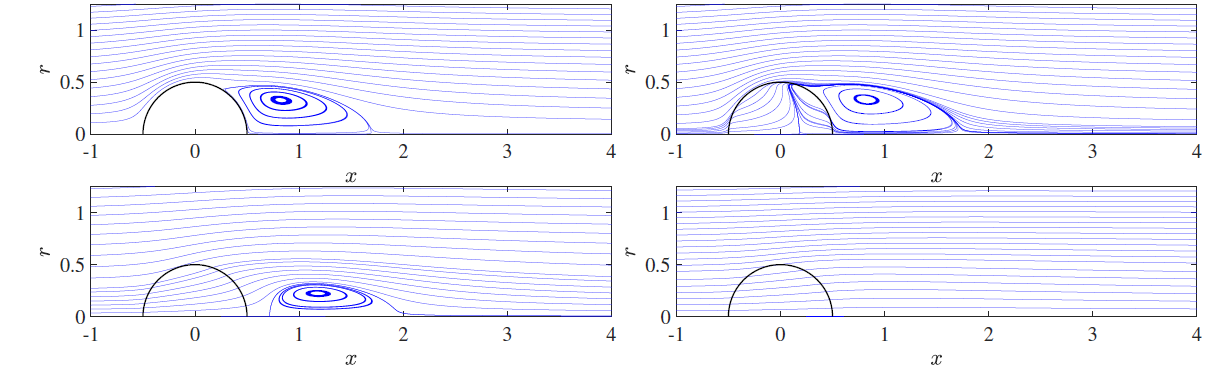
Figure 2: Velocity field streamlines for the steady and axisymmetric flow around and through a porous sphere (cut at one azimuthal section).
In this project, we study the effect of the porosity on a porous sphere invested by a uniform flow, at low velocities. We focus on the properties of the steady and axisymmetric solution of the flow equations. The flow in the porous structure is modeled by employing a Darcy-Brinkman approximation [3].
The first part involves a characterization of the aerodynamic properties (drag, length of the recirculation region, etc.) when a constant (figure 2) and variable porosity of the body is imposed, together with a characterization of the stability properties of the flow.
The second part then focuses on the study of the sensitivity of the flow to porosity variations of the sphere, to maximize objective functions when some constraints are imposed. The study will be carried out using a Lagrangian approach [4].
The third part consists in the derivation of a porous structure which approximates the porosity and permeability requirements, and in a numerical comparison of direct numerical simulations with the porous model.
The numerical codes for the steady flow and the stability analysis will be provided, together with the literature needed to derive the sensitivity analysis. The student will be supported during the derivation of the theoretical tools and the modification of the codes for the second and third part.
Numerical skills: Knowledge of MATLAB. The rudiments of FreeFem++ will be given.
Key words: flow control, porous bodies, aerodynamic instability, sensitivity analysis
Supervisor: Pier Giuseppe Ledda
[1] Cummins, C., Seale, M., Macente, A., Certini, D., Mastropaolo, E., Viola, I. M., & Nakayama, N. (2018). A separated vortex ring underlies the flight of the dandelion. Nature, 562(7727), 414-418.
[2] Ledda, P. G., Siconolfi, L., Viola, F., Camarri, S., & Gallaire, F. (2019). Flow dynamics of a dandelion pappus: A linear stability approach. Physical Review Fluids, 4(7), 071901.
[3] Ledda, P. G., Siconolfi, L., Viola, F., Gallaire, F., & Camarri, S. (2018). Suppression of von Kármán vortex streets past porous rectangular cylinders. Physical Review Fluids, 3(10), 103901.
[4] Boujo E., An adjoint-based approach to the optimal control of separated flows. EPFL PhD thesis https://infoscience.epfl.ch/record/200987?ln=fr