Type : Master’s project
Description :
A shallow corral surrounding a circular cylindrical reservoir is used as a damper for suppressing sidewall non-ideality effects, i.e. meniscus or edge) waves, in liquid sloshing dynamics. For instance, when the container undergoes a vertical periodic motion, the capillary oscillating meniscus emits edge waves. These waves, which appear as concentric ripples (see Figure 1 below), travel from the lateral solid wall towards the container center and reflect back, hence perturbing the free surface that appears no more flat. As they represents a perturbation from the ideal flat surface configuration, such meniscus waves are strongly undesired in typical experimental settings and, therefore, they must be somehow annihilated. The idea behind the use of a shallow surrounding corral is that in this thin layer of fluid, inertia is essentially suppressed, so that meniscus waves are rapidly damped out before reaching the fluid bulk in the actual inner cylindrical basin, where, as desired, the free liquid surface remains nearly flat.
Scope :
The main goal of this project consists in computing the system response to a vertical harmonic forcing in presence of a curved meniscus, whose static profile shape is dictated by two parameters, i.e. the Bond number, Bo, and the static contact angle, θ_s, which, in this project, will be systematically varied. The outcomes of such an analysis will be then used to design an experimental setting, in particular, to select the fluid and the two main geometrical parameters L and D, in order to achieve a setup capable of guaranteeing the suppression of unwanted meniscus waves.
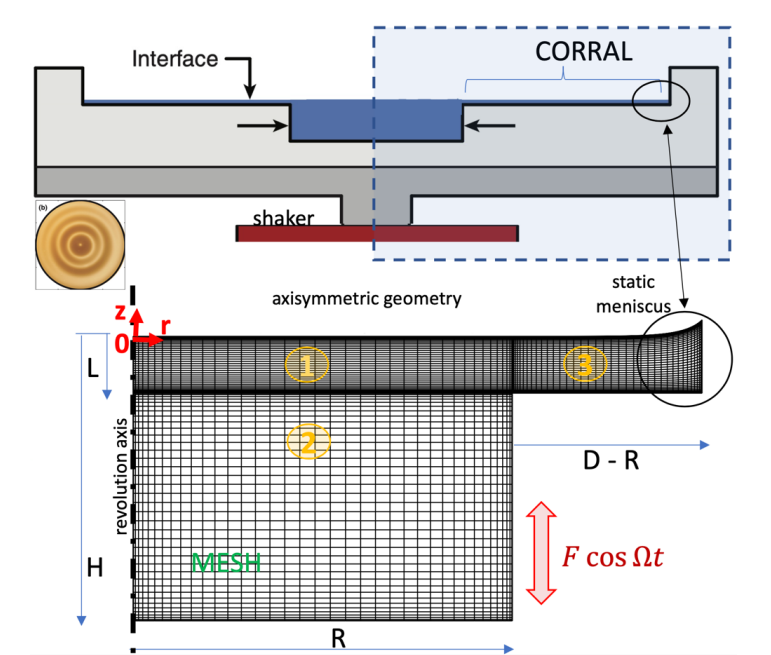
Bottom: Representation of a numerical mesh obtained via pseudospectral discretization technique (Gauss-Lobatto-Chebyshev polynomials). For practical implementation reasons, the computational domain is decomposed in three sub-domains, 1, 2 and 3 in the figure above, with the imposition of proper matching conditions at each boundaries. The nominal container radius is denoted by R, the outer radius is D-R, whereas the fluid depth is H. L denotes the height of computational domain 1
Numerical tools :
1) Chebyshev-based pseudospectral collocation method with sub-domain decomposition implemented in Matlab. This will be used to compute the linear system harmonic response in the limit of small forcing amplitude, F≪1;
2) Fully nonlinear axisymmetric simulation performed in COMSOL.
Preliminary Matlab and COMSOL scripts (to be slightly modified if required) are provided to the
student.
Supervisors : Alessandro Bongarzone & François Gallaire