Neural networks for reliable learning and control
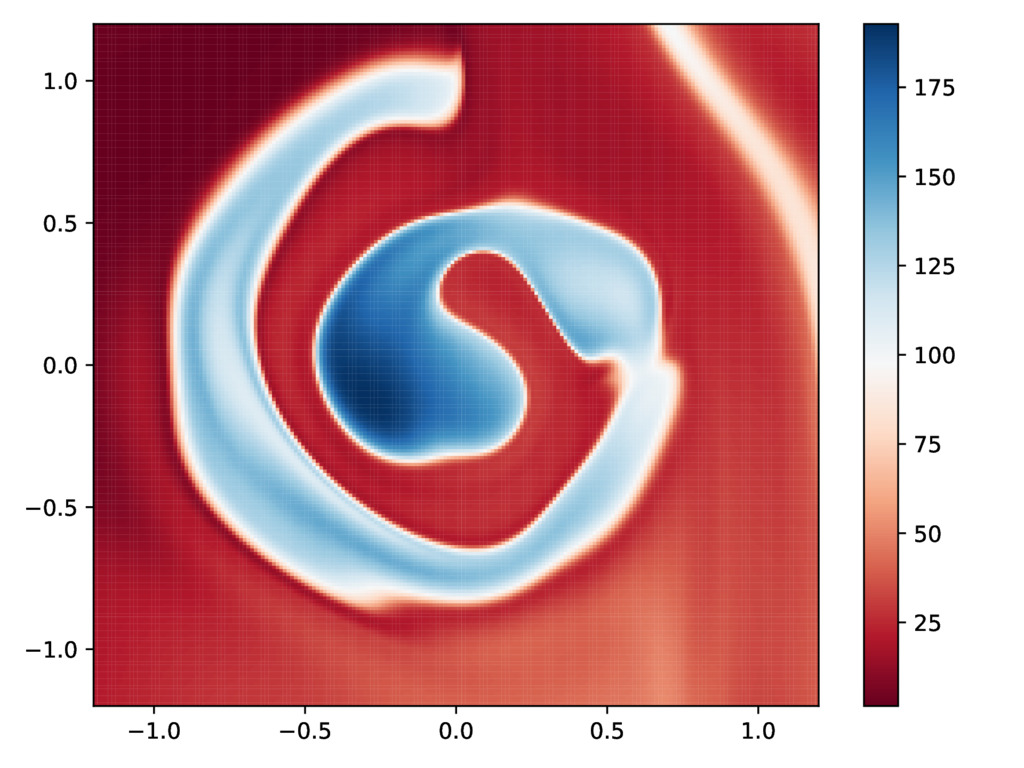
We develop deep networks inspired by dynamical systems for machine learning tasks. Our architectures do not suffer from vanishing gradients during training and can be endowed with contractivity properties that make them robust against noise and attacks on test data.
Furthermore, we study how to use ODE-based neural networks for parametrizing rich sets of controllers for complex plants. Our primary interest is to formally guarantee dependability of the closed-loop dynamics, even if the learning phase stops prematurely. A related goal is to characterize all regulators stabilizing a given nonlinear system by parametrizing the achievable closed-loop maps. Our results pave the way to the design of neural network controllers that minimize a general nonlinear cost without spoiling the stability of the system.
Current research lines also embrace (1) the study of federated learning algorithms for learning from client local data while fulfilling strict privacy constraints and (2) the development of new zeroth-order optimization methods for constrained optimization in presence of unknown costs and constraints.
Control of complex systems
We focus on systems stemming from the interconnection of several subsystems and develop distributed control, state estimation, and fault detection algorithms exploiting local computational resources and communication networks. We are especially interested in scalable design procedures, where the complexity of local synthesis is independent of the total number of subsystems and, nevertheless, global properties such as stability and reliability can be guaranteed.
In our previous research, we formalized the concept of plug-and-play (PnP) design and proposed various PnP control methods. In order to improve resiliency to unexpected phenomena, recently we have extended the principles of PnP design to the synthesis of distributed state observers and fault detection schemes. The goal is to perform the automatic reconfiguration of control architectures so as to improve the dependability of the system. We applied our methods to frequency control in power networks and to the stabilization of large-scale mechanical systems. These examples are included in the Plug and Play Model Predictive Control (PNPMPC) toolbox for MatLab.
We also consider the design of controllers and state estimators based on regret measures, which adapt to disturbance profiles that are neither Gaussian nor worst-case. We showed that, for linear systems, the design can be performed through convex optimization, which paves the way for the introduction of safety constraints in the synthesis problem.
Microgrids and distribution networks with flexible structure
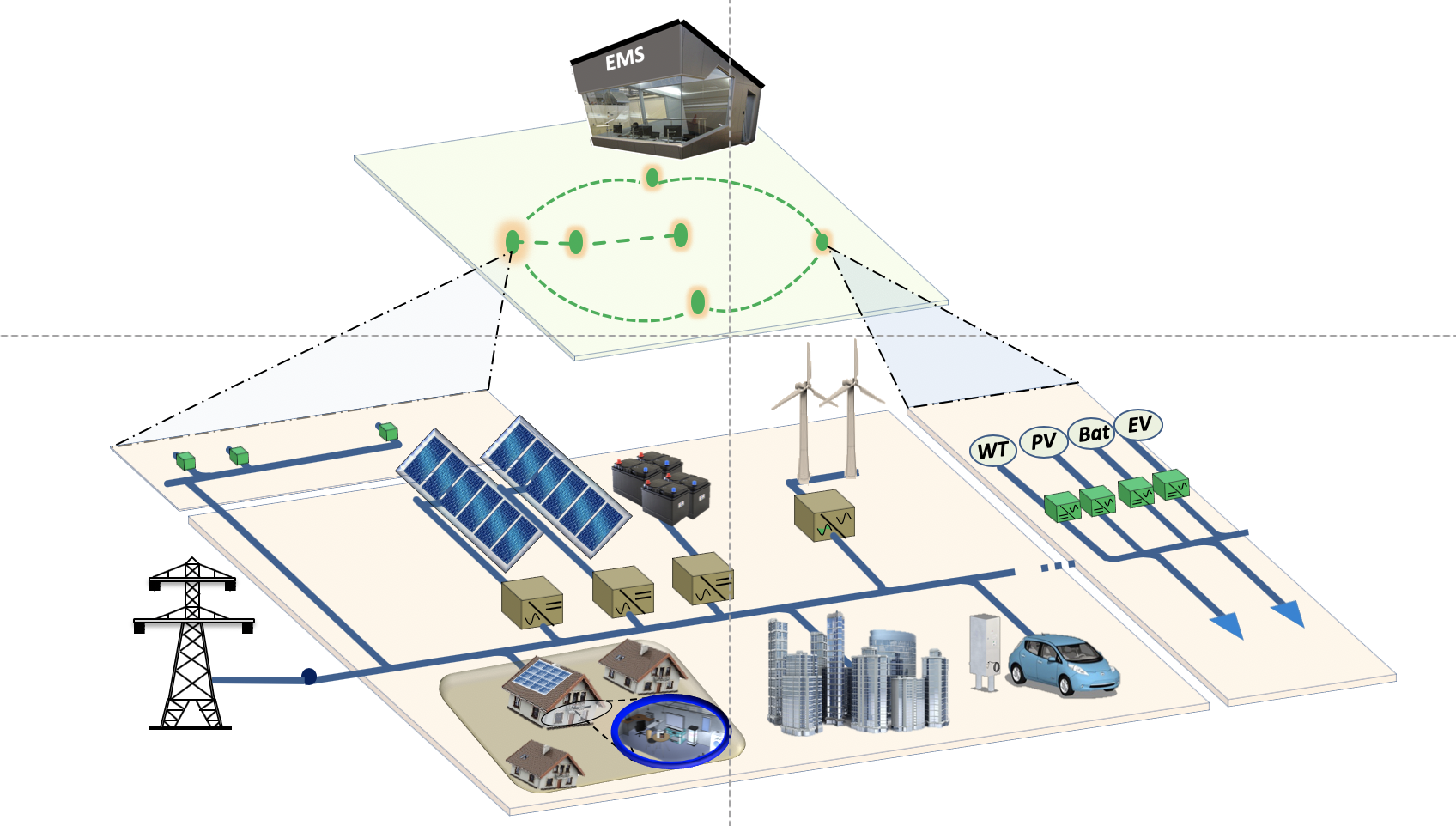
Microgrids are electric networks composed by the tight interconnection of generation units, lines, and loads. Besides fostering the use of renewables, microgrids can provide autonomous electric islands of varying sizes and topologies, where generators and loads are added and removed over time. The control of microgrids is a complex problem involving several objectives and spanning multiple time scales.
Our research focuses on the development of hierarchical control schemes for DC and AC microgrids. Past results include the derivation of scalable algorithms for the plug-and-play design of primary voltage regulators, the development of secondary controllers based on consensus protocols, and the study of energy management systems, sitting at the tertiary layer.
To improve safety, we also developed distributed algorithms for detecting cyberattacks on the communication network between generation units and for triggering reconfiguration strategies.
We also proposed novel algorithms for reconstructing the topology and parameters of distribution networks based on available data collected by micro PMUs or smart meters. The final goal will be to develop energy management systems that self-adapt to changes in the underlying grid topology.