This conference is associated to the annual meeting of the Swiss Mathematical Society, held on 16 June 2022 on campus, where Claire Voisin gives the plenary talk.
Please register, if you plan to attend, even if you do not request a hotel room, or financial support. This way we would have a precise idea about how may participants to expect. The link to the registration form is here.
Location:
- all lectures will be in CE 1 6
- all coffee breaks and the Tuesday and Thursday evening catering diners will be in the Bernoulli Center, in GA 3 35
- in the breaks the seminar room GA 3 21 of the Bernoulli Center can be used for discussions and for working
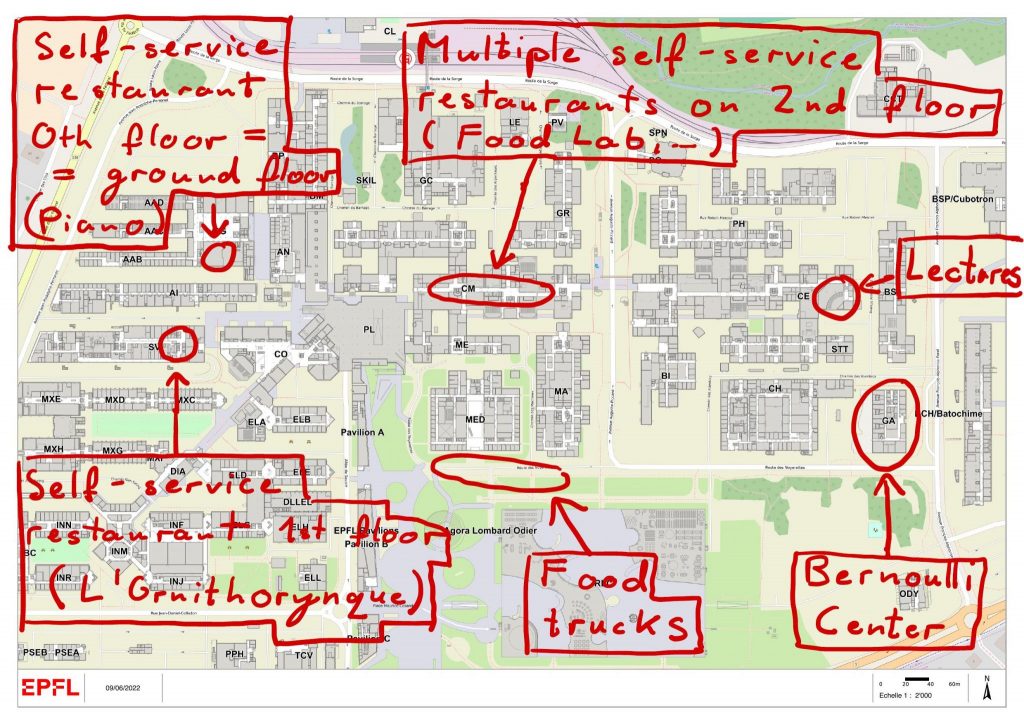
- for lunch, we plan with participants using any of the campus eateries or the food-trucks, or even one of the coffee shops in case of a light lunch. A map of some of the different options is:
Schedule:
13 June
9:00-10:00 Fabio Bernasconi
Title: Lifting globally $F$-split surfaces to characteristic 0
Abstract: Given a projective variety X over an algebraically closed field k of characteristic p>0, it is natural to understand the possible geometric and arithmetic obstructions to the existence of a lifting to characteristic zero.
Motivated by the case of abelian varieties and K3 surfaces, a folklore conjecture asserts that ordinary Calabi-Yau manifolds lift over the ring of Witt vectors W(k).
I will report a joint work with I. Brivio, T. Kawakami and J. Witaszek where we prove that globally F-split surfaces (a generalisation of ordinary CYs) admit an equi-singular lifting over W(k).
From this we deduce several geometric consequences for F-split surfaces, as the Bogomolov bound on the singular points of klt del Pezzos.
10:00-10:45 coffee break
10:45-11:45 Luca Tasin
Title: Sasaki-Einstein metrics on spheres
Abstract: I will report on a joint work with Yuchen Liu and Taro Sano in which we construct infinitely many families of Sasaki-Einstein metrics on odd-dimensional spheres that bound parallelizable manifolds, proving in this way conjectures of Boyer-Galicki-Kollár and Collins-Székelyhidi. The construction is based on showing the K-stability of certain Fano weighted orbifold hypersurfaces.
12:00-13:00 Susanna Zimmermann
Title: Real birational involutions of the plane
Abstract: Birational involutions of the plane over a closed field have been classified up to conjugation by Bayle-Beauville. They are conjugate to linear maps, to involutions preserving a pencil of lines, to Geiser involutions or to Bertini involutions. Moreover, in the non-linear case, the fixed curve determines the conjugacy class. The classification is still open over non-closed fields, and I will present what we know over the real numbers, which is a collaboration with I. Cheltsov, F. Mangolte and E. Yasinsky. For instance, unsurprisingly, it is not true anymore that the fixed curve determines the conjugacy class.
13:00-14:30 Lunch break
14:30-15:30 Adrien Dubouloz
Title: Affine spaces in Mori fiber spaces
Abstract: (Based on joint work with Takashi Kishimoto, Masaru Nagaoka and Karol Palka). I will survey a collection of techniques to construct completions of affine spaces of various dimensions in total spaces of mildly singular Mori fiber spaces over the projective line. As illustrations, I will explain on the one hand the construction of completions into Mori fibers spaces whose general fibers are non-rational Fano varieties of Picard rank one, and on the other hand constructions of completions of the affine 3-space into total spaces of del Pezzo fibrations with terminal singularities.
15:30-16:15 coffee break
16:15-17:15 Jean-Philippe Furter
Title: Degenerations of Cremona transformations
Abstract: Denote by Bir(P^2) the plane Cremona group. If X is an algebraic variety, Demazure and Serre have defined what is a morphism from X to Bir(P^2). In this lecture, we will study some of the properties satisfied by such maps. This a joint work with J. Blanc.
14 June
9:00-10:00 Hamid Abban
Title: K-stability of Fano hypersurfaces
Abstract: K-stability is an algebraic notion that detects existence of Kähler-Einstein metrics on Fano varieties. In recent years K-stability has found a life of its own within algebraic geometry with developments in K-moduli theory as well as explicit methods. In this talk, I will give an overview of the subject with an emphasis on new methods of checking stability based on valuative criteria. A guiding class of examples throughout the talk will be Fano hypersurfaces and their K-stability. This is based on joint work with Ziquan Zhuang.
10:00-10:45 coffee break
10:45-11:45 Anne-Sophie Kaloghiros
Title: 1-dimensional K-moduli spaces of Fano 3-folds
Abstract: Recent advances in the study of K-stability have shown that there is a projective good moduli space of K-polystable Q-Gorenstein smoothable Q-Fano varieties of dimension n and volume V.
The classification of smooth Fano 3-folds is due to Iskovshikh, Mori and Mukai and dates back to the 80s. While the classification is non-modular, it contains rich information on the geometry of Fano 3-folds. Fano 3-folds offer a rich source of examples in which we can explicitly construct and understand some K-moduli spaces.
In this talk, I will discuss some examples of 1-dimensional K-moduli spaces of Fano 3-folds.
This is joint work with Abban, Cheltsov, Jiao, Martinez-Garcia, Papazachariou and Sarikyan.
12:00-13:00 Paolo Cascini
Title: On the Minimal Model Program for algebraically integrable foliations
Abstract: Every fibration, or more in general, every dominant rational map between normal varieties, defines a natural foliation, which is called algebraically integrable. The canonical sheaf of such a foliation behaves, in many aspects, as the canonical sheaf of a normal variety. I will describe some recent results in this direction, such as a cone theorem, and some applications on the canonical bundle formula. In particular, this provides a proof of a conjecture by Shokurov. This is joint work with Ambro, Shokurov and Spicer.
13:00-14:30 Lunch break
14:30-15:30 Ana-Maria Castravet
Title: Blown up toric surfaces with non-polyhedral effective cone
Abstract: I will discuss joint work with Antonio Laface, Jenia Tevelev and Luca Ugaglia on constructing examples of projective toric surfaces whose blow-up at a general point has a non-polyhedral pseudo-effective cone, both in characteristic 0 and in every prime characteristic p. As a consequence, we prove that the pseudo-effective cone of the Grothendieck-Knudsen moduli space of stable rational curves with n markings is not polyhedral for n>=10.
15:30-16:15 coffee break
16:15-17:15 John Ottem
Title: Some new examples of O-acyclic varieties with no C(t)-points
Abstract: In this talk, I will survey a few results about C(t)-points on O-acyclic varieties. Here a variety is said to be O-acyclic if the higher cohomology groups of the structure sheaf vanish; examples include rationally connected varieties, Enriques surfaces and fake projective planes. A fundamental question, going back to Serre, ask whether such varieties always admit points defined over the function field of a complex curve. In the talk I will outline a few new counterexamples to this question, and also discuss some positive results. This is based on joint work with Alberg and Suzuki.
18:30- Catering dinner
15 June
9:00-10:00 Enrica Floris
Title: On the moduli part of a klt-trivial fibration
Abstract: Let f: (X,B)->Y be a fibration such that the log-canonical divisor K+B is trivial along the fibres of f. The canonical bundle formula is a way of expressing K+B as the pullback of the sum of three divisors: the canonical divisor on Y; a divisor, called discriminant, carrying informations on the singular fibres; a divisor called moduli part keeping track of the birational variation of the fibres and having positivity properties.
Let T be a connected, reduced but not necessarily irreducible divisor of Y.
In this talk I will give a geometric interpretation of the semiampleness of the restriction of the moduli part to T and give some results towards the semiampleness of the restriction.
10:00-10:45 coffee break
10:45-11:45 Lukas Braun
Title: Reductive quotients of klt varieties
Abstract: In this talk, I will explain the proof of the recent result, obtained together with Daniel Greb, Kevin Langlois, and Joaquin Moraga,that reductive quotients of klt type varieties are of klt type. If time permits, I will also discuss several applications of our result, e.g. on quotients of Fano type varieties, good moduli spaces, and collapsing of homogeneous bundles.
12:00-13:00 Michel Brion
Title: Weil’s regularization theorem and beyond
Abstract: A theorem of Weil asserts that every rational action of a smooth algebraic group G on a smooth algebraic variety X can be regularized, in the sense that there exists variety Y equipped with a regular action of G and with an equivariant birational isomorphism to X. In the talk, we will present additional results: the model Y may be taken projective and normal, and the regularization theorem extends to non-smooth algebraic groups. We will also discuss some applications to rational actions on curves and surfaces.
13:00-14:30 Lunch break
14:30-15:30 Claire Voisin
Title: On the coniveau of rationally connected threefolds
Abstract: We prove that that the integral cohomology modulo torsion of a rationally connected threefold comes from the degree 1 cohomology of a smooth projective curve via a family of 1-cycles. Equivalently, it is of strong coniveau 1, following the terminology of Benoist-Ottem.
15:30-16:15 coffee break
16:15-17:15 Christian Urech
Title: Actions of Cremona groups on CAT(0) cube complexes
Abstract: Recently, in geometric group theory, isometric actions of groups on CAT(0) cube complexes have turned out to be powerful tools to study a
broad range of groups. In this talk, I will explain the construction of
CAT(0) cube complexes on which groups of birational transformations act
by isometries and explain how to use these actions to deduce new and old
group theoretical and dynamical results about Cremona groups. This is
joint work with Anne Lonjou.
16 June
9:00-10:00 Andrea Fanelli
Title: A question on the real locus of smooth Fano threefolds
Abstract: Smooth complex Fano threefolds have been fully classified by Iskovskikh and Mori-Mukai and their description is well understood and rather explicit. In this context it is natural to study the geometry of real smooth Fano threefolds and to investigate the connections between their algebraic properties and topological properties of their real loci.
In this talk I will survey some known results and present a joint work in progress with Frédéric Mangolte, in which we investigate the connectedness of the real locus for smooth Fano threefolds.
10:00-10:45 coffee break
10:45-11:45 Nikolaos Tsakanikas
Title: The Nonvanishing problem for varieties with nef first Chern class
Abstract: Let X be a threefold with mild singularities such that c1(X) is nef. In this talk I will present a proof that then the numerical class of c1(X) is effective. This result (joint work with Vladimir Lazić, Shin-Ichi Matsumura, Thomas Peternell, and Zhixin Xie) is the positive curvature counterpart of the famous result of Miyaoka from the 1980s, which showed that –c1(X) is effective as soon as it is nef.
12:00-13:00 Stéphane Druel
Title: Projectively flat log smooth pairs
Abstract: In this talk, I will discuss projective log smooth pairs with numerically flat normalized logarithmic tangent bundle. Generalizing works of Jahnke-Radloff and Greb-Kebekus-Peternell, we show that, passing to an appropriate finite cover and up to isomorphism, these are the projective spaces or the log smooth pairs with numerically flat logarithmic tangent bundles blown-up at finitely many points away from the boundary. On the other hand, the structure of log smooth pairs with numerically flat logarithmic tangent bundle is well understood: they are toric fiber bundles over finite etale quotients of abelian varieties.
13:00-14:30 Lunch break
14:30-15:30 Emanuele Macri
Title: Lagrangian fibrations on hyper-Kähler fourfold
Abstract: I will present joint work with Olivier Debarre, Daniel Huybrechts and Claire Voisin on the SYZ hyper-Kähler conjecture for fourfolds under certain topological assumptions.
As application, this proves a conjecture by O’Grady that a hyper-Kähler fourfold whose cohomology ring is isomorphic to the one of the Hilbert square of a K3 surface is a deformation of a Hilbert square.
15:30-16:15 coffee break
17:00-18:00 Claire Voisin’s colloquium
Title: On the complex cobordism classes of hyper-Kähler manifolds
Abstract: Hyper-Kähler manifolds are symplectic holomorphic compact Kähler manifolds, a particular class of complex manifolds with trivial canonical bundle. They exist only in even complex dimension, and there are two main series of known deformation classes of hyper-Kähler manifolds, with one model in each even dimension, that I will describe. I will discuss in this introductory talk a result obtained with Georg Oberdieck and Jieao Song on the complex cobordism classes of hyper-Kähler manifolds, and present a number of open questions concerning their Chern numbers.
18:30- Catering dinner
17 June
9:00-10:00 Egor Yasinsky
Title: Birational automorphisms of Severi-Brauer surfaces, with applications to Cremona groups of higher ranks
Abstract: A Severi-Brauer surface over a field k is an algebraic k-surface which is isomorphic to the projective plane over the algebraic closure of k. We describe the group of birational transformations of a non-trivial Severi-Brauer surface over a perfect field k, proving that in most cases it is not generated by elements of finite order as it admits a surjective group homomorphism to Z. We then use this result to show that complex Cremona groups of rank at least 4 admits a surjective homomorphism to a free group over C (the field of complex numbers). In particular, any group of cardinality at most the one of C appears as the quotient of the Cremona group of rank 4. As a consequence, this gives a negative answer to the question of Dolgachev of whether the Cremona groups of all ranks are generated by involutions. Based on a joint work with J. Blanc and J. Schneider.
10:00-10:45 coffee break
10:45-11:45 Evgeny Shinder
Title: Motivic invariants of birational maps
Abstract: I will explain invariants of birational maps taking values in the free abelian groups of birational types, and deduce that various Cremona groups are not generated by elements of finite order. This is joint work with H.-Y. Lin.
12:00-13:00 Sofia Tirabassi
Title: Characterization of quasi-abelian surfaces
Abstract: We give a characterizations of auasi-abelian surfaces analogue to the characterizations of abelian surfaces of Enriques and Chen–Hacon. This is a joint work with M. Mendes Lopes and R. Pardini
13:00-14:30 Lunch break
14:30-15:30 Roberto Svaldi
Title: A geometric characterization of toric singularities and toric morphisms
Abstract: When considering germs of singularities, it is natural to try to determine and study numerical invariants that may characterise certain special types of singularities.
For example, Shokurov conjectured that the fact that a germ of a singularity $x \in X$ is analytical isomorphic to the germ of a toric singularity should be completely detectable by the vanishing of a certain numerical invariant, called complexity. The complexity can be defined in the terms of how many divisors can pass through the point $x$ without creating a singularity worst than log canonical, where we also take into account the dimension of the span of the components of a divisor in the local class group of $X$ at $x$.
Actually, Shokurov’s conjecture is way more general: it claims that a suitable analogue of the complexity, that is still defined in terms of divisors and the cohomological span of their components, should classify all germs of proper morphisms with connected fibres that are analytically isomorphic to a proper contraction of toric varieties.
I will explain how a general solution to Shokurov’s conjecture can be given. Moreover, I will explain how the strategy of such solution is inspired by and carried out using a local-to-global principle in birational geometry that has been developed over the last decade. Such principle allows us to link the local structure of germs of klt singularities to the global structure of a projective log Fano pair, via a so-called pet blow-up.
This talk is based on joint work with M. Brown, J. McKernan, R. Zong, and with J. Moraga.
15:30-16:15 coffee break
16:15-17:15 Stefano Filipazzi
Title: On the boundedness of elliptic Calabi-Yau threefolds
Abstract: In this talk, we will discuss the boundedness of Calabi-Yau threefolds admitting an elliptic fibration. First, we will review the notion of boundedness in birational geometry and its weak forms. Then, we will switch focus to Calabi-Yau varieties and discuss how the Kawamata-Morrison cone conjecture comes in the picture when studying boundedness properties for this class of varieties. To conclude, we will see how this circle of ideas applies to the case of elliptic Calabi-Yau threefolds. This talk is based on work joint with C.D. Hacon and R. Svaldi.
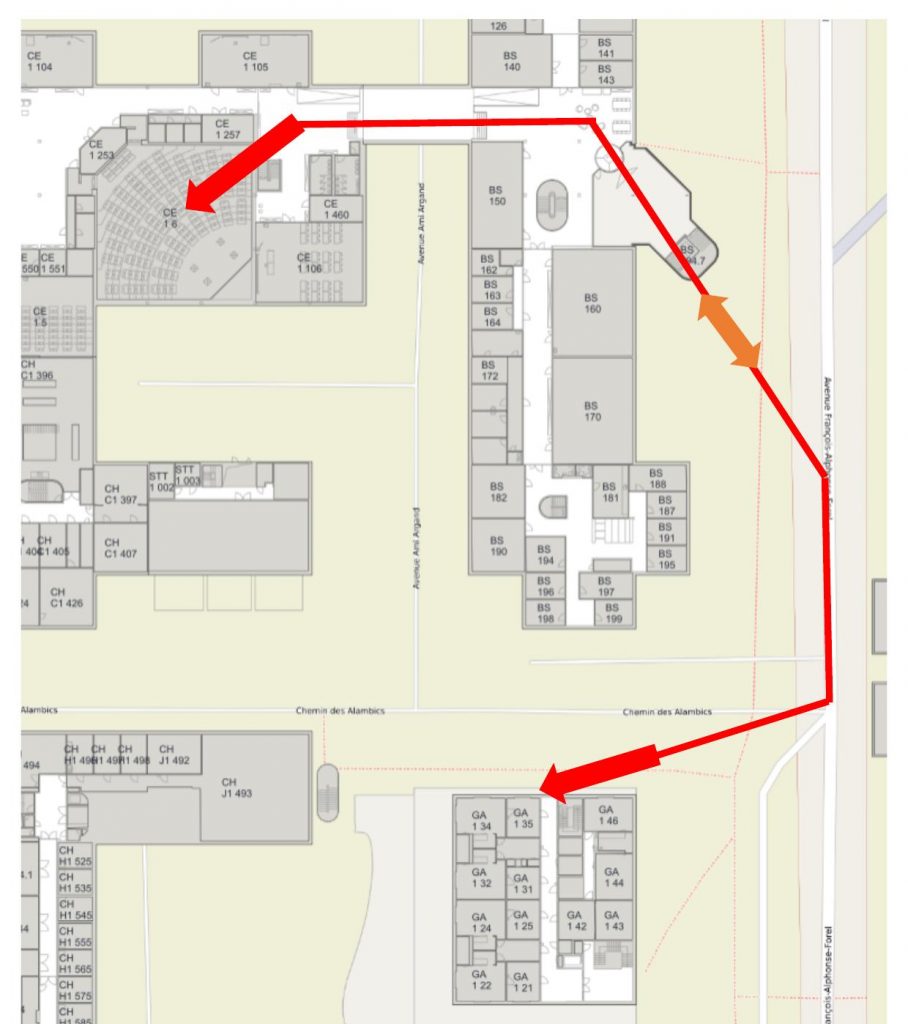
Access map between CE 1 6 and the Bernoulli Center:
Support:



–Organizers: Jérémy Blanc, Zsolt Patakfalvi