Chair of Arithmetic Geometry
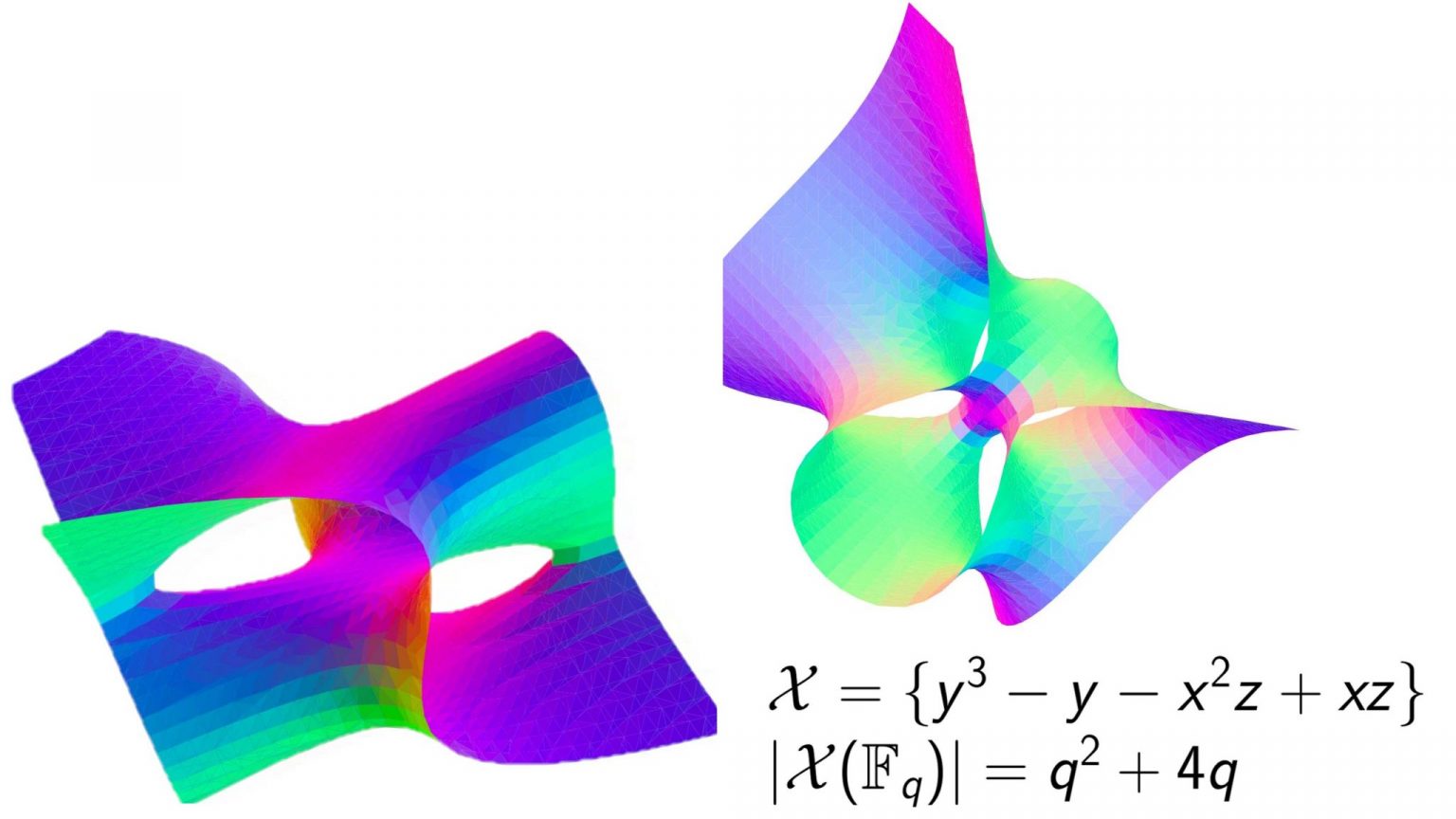
At the chair of arithmetic geometry we study the interplay between algebraic geometry and number theory. Concretely we are interested in the geometry and topology of algebraic varieties, which are roughly speaking solution sets of polynomial equations. Through the famous Weil conjectures, proven by Deligne, we can get information about the geometry of those equations by counting their solutions over finite fields.
The algebraic varieties we consider are often moduli spaces, that is parameter spaces for certain objects such as Higgs bundles or quiver representations. These objects arise in different contexts notably in representation theory, number theory and mathematical physics and counting them often leads to surprising connections between those seemingly different fields.
Recently we have focused a on a technique called p-adic/motivic integration, which allows us to count points through a p-adic analytic deformation. While we managed to apply this approach to various problems, many aspects of p-adic integration remain unclear and have yet to be discovered.
Contact
EPFL SB MATH ARG
MA C3 605 (Bâtiment MA)
Station 8
CH-1015 Lausanne