Public interest in ancient cultures has never been as strong as it has been in recent decades, thanks to easier access and the development of tourism policies implemented by governments. However, modern visitor numbers to these sites are reaching levels that are incomparable to their original use; their conservation and restoration often exceed the framework defined by the Venice Charter. At the heart of economic issues, the exploitation of these sites often takes precedence over their study. Under these conditions, it seems urgent to analyse this category of highly visited buildings in order to enable their scientific preservation. The temple of Kom Ombo, located on the Nile cruise route, is one of the must-see stops for many visitors (thousands per day). It is therefore directly affected by issues of wear and tear, maintenance and conservation of structures.
The architectural analyses will be carried out in parallel with the survey and will be done in two stages. First, we will analyse the spaces (solid and empty), the structural elements (assembly with mortar and staples, crypts, lighting, roof slabs, lintels and architraves), horizontal and vertical circulation, and their restoration. Then, in a second stage, we will carry out static analyses that will provide information on the building’s resistance to earthquakes and differential settlement. The same type of analysis has been carried out for other temples, which will allow for comparative studies. It is clear that the builders were aware of the damage caused by the juxtaposition and superimposition of different built volumes (naos and pronaos) and took measures to limit the damage.
This second part of the study will be carried out using mechanical analyses and numerical simulations in collaboration with the LSMS (Laboratory of Solid Mechanics) laboratory headed by Professor Jean-François Molinari. This collaboration will consist of the co-supervision of a master’s project, during which the student will carry out finite element simulations of archaeological structures in relation to the soil. This work will be carried out in collaboration with Raphael Vouilloz, who is in charge of BIM modelling of the temple.
Supervisors:
Aurélie Terrier, Jean-François Molinari

Project summary
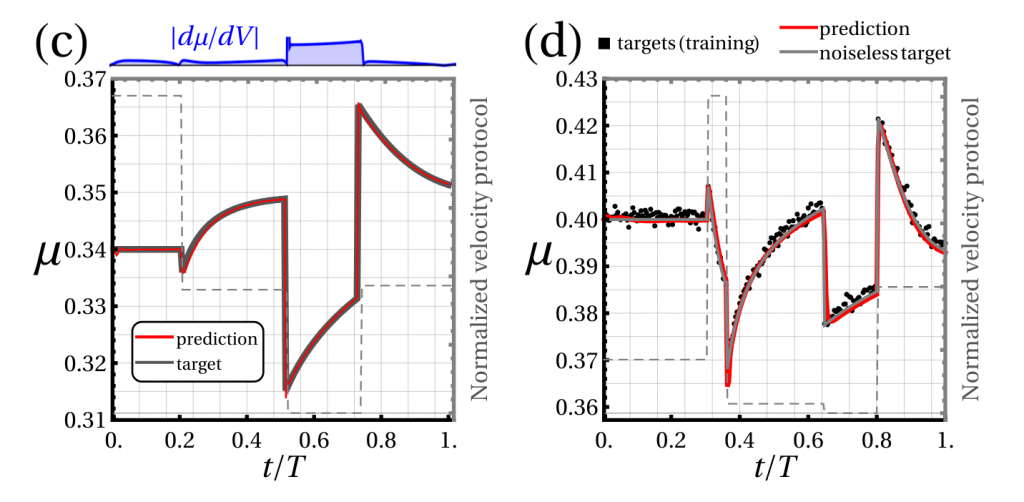
We aim to design manufacturable surface topographies that produce a prescribed static-friction vs. load curve. Because static friction is (approximately) proportional to the real contact area between asperities, the problem reduces to generating surfaces whose contact area A(L) follows a target function of applied load L.
Problem statement
-
Feasible behaviors: What classes of A(L) (and thus friction-load curves) are physically realizable under elastic/plastic contact?
-
Manufacturing constraints: What limits on feature size, height range, spacing, and aspect ratio keep the design practical to machine or print?
Research directions (pick based on interest)
-
Asperity geometry -> loading curves: How do shape, height distribution, and spacing of bumps control A(L)?
-
Inter-asperity interactions: When do neighboring features couple (shielding, coalescence) and how does that change contact evolution?
-
Onset of new contacts: Can we create a rigorous mathematical model for the incremental change in A when a fresh asperity first makes contact?
-
Inverse design with ML: Can a neural network infer surface parameters from a specified A(L) or friction-load curve?
-
Application to sports gear: Use the framework to design tunable-friction surfaces (e.g., table-tennis rackets) under real manufacturing limits.


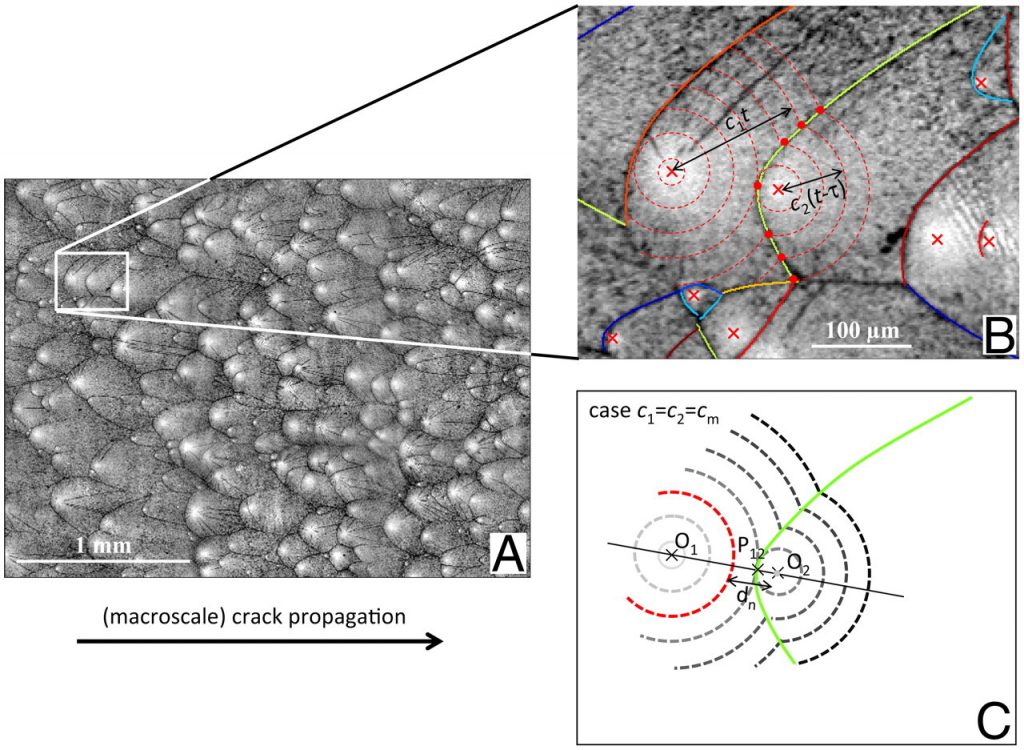
Earthquakes can be devastating, both in terms of human and material damage. Although their existence has been known since the dawn of time, the physics of earthquakes is still poorly understood. Natural faults and earthquake characteristics are known to follow scaling power-law. The origin of this phenomenon has strong implications on the physical mechanisms driving slip events. However, it is not yet clear. The emergence of complexity can be related to the disorder of the system. Understanding if the observed complexity comes from the inherent complexity of the frictional motion or the system’s complexity is essential to better understand – and one day eventually predict – earthquakes. It has been shown numerically with a simple system without any disorder that resulting slip events follow a power-law distribution for the small events – like natural slip events – and a log-normal distribution for the larger ones. This project aims to study how adding disorder in this simple system will influence the transition between the power-law and the log-normal distribution of slip events. To do so, the student will use a finite element software developed in the lab (Akantu).
Supervisors:
Ferry Roxane Mathilde Suzanne, Jean-François Molinari

This project seeks to combine the traditional finite element method with new machine-learning tools. The tentative goals are, first, to analyze new methods recently proposed in the literature; (e.g., the “Deep Ritz Method”) and, second, to adapt them to solve large-deformation problems in simple geometries.
Supervisors:
Joaquin Garcia Suarez, Jean-François Molinari
Wave propagation is a well-understood phenomenon, but gripping complexity can arise from it when it takes place within a layered medium, due to the continuous reflection, transmission and superposition of what originally may have been a coherent wavefront. On this topic, we propose two types of projects: (1) mostly theoretical ones (intended for students with a taste for applied mathematics) aimed at exploring how abstract algebra can help to unravel this complexity, (2) mostly numerical ones (for students interested in coding and simulations) aimed at implementing and testing new methods to simulate wave propagation in structured materials.
Supervisors:
Joaquin Garcia Suarez
The disruptive work of Karniadakis and colleagues has created a new way to find approximate solution of ODEs and PDEs with relevance to physics and engineering. In this project, we would seek to survey the most efficient ways to train PINNs, and apply these findings to solve problems featuring stick-slip: . If the student is interested, a mathematical twist is also possible by focusing on analyzing the convergence and error estimates of PINNs.