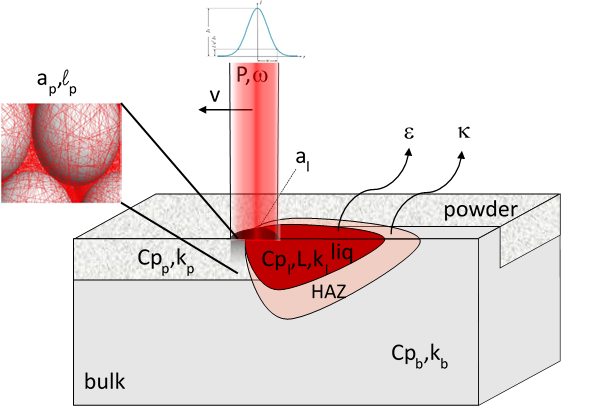
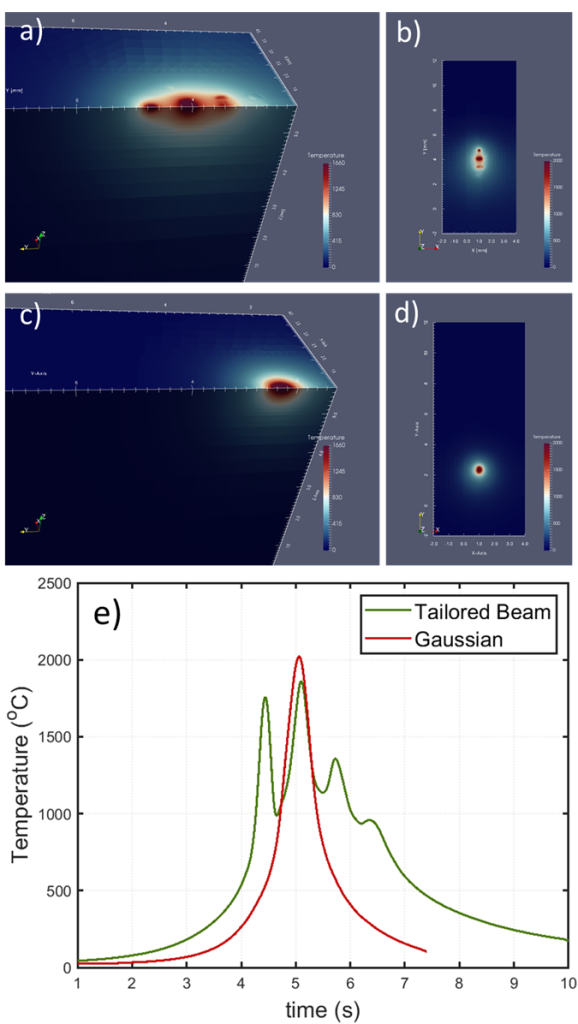
Des simulations numériques du processus LPBF (pour Laser Powder Bed Fusion) sont effectuées avec un code à éléments finis (FEM) développé en interne par Dr. Eric Boillat. Le transfert de chaleur est décrit par l’évolution de deux champs: l’enthalpie par unité de masse et la température.
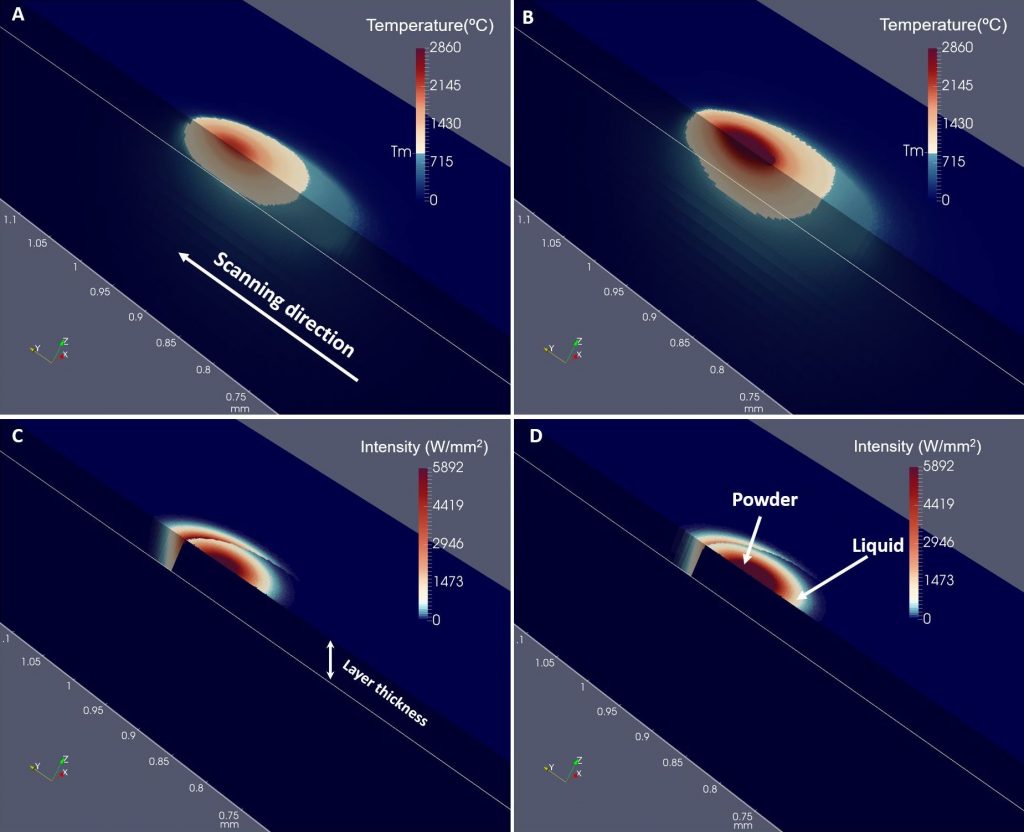
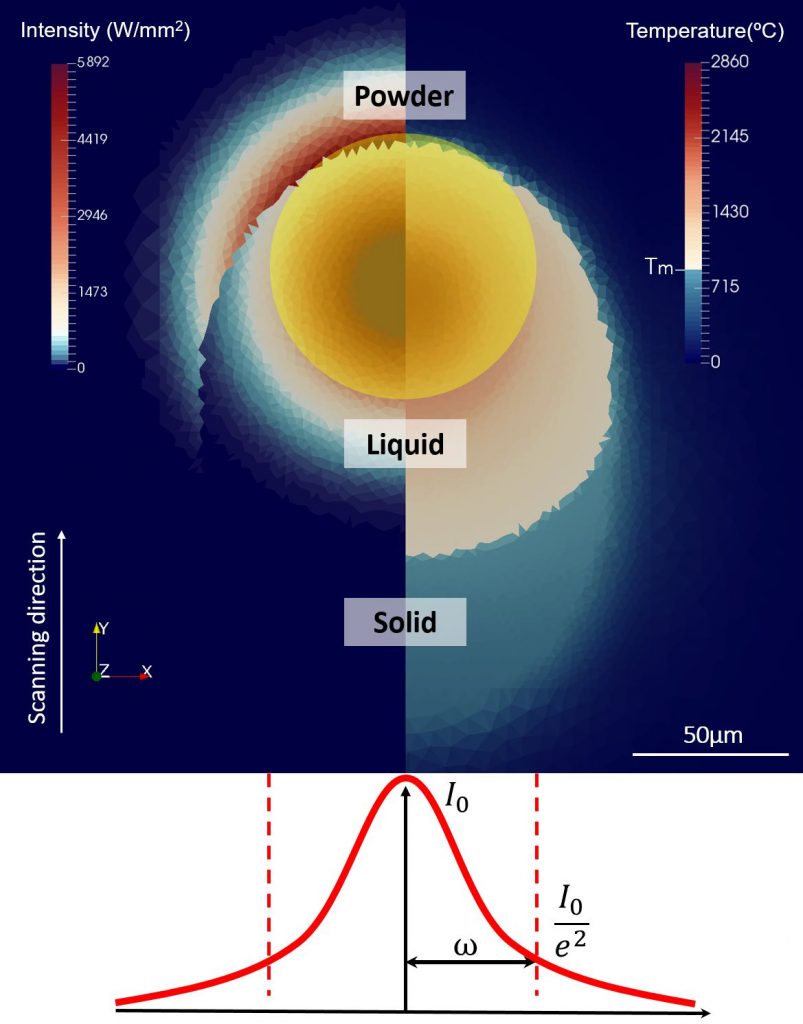
Le faisceau laser est modélisé comme une source de chaleur superficielle pour le plein et le liquide et une source de chaleur volumique pour les poudres. Le lit de poudre est considéré comme un milieu homogène avec des propriétés moyennes (dites efficaces) telles que l’absorptivité, la conductivité thermique, la profondeur de pénétration optique, la densité.
Le maillage se compose d’un maillage grossier fixe sur l’ensemble du domaine et d’un maillage mobile fin autour du spot laser pour obtenir la précision nécessaire pour le calcul de la conduction thermique dans la poudre et à l’interface entre la poudre et le solide plein ou le liquide.

Pour une description précise du processus LPBF, un nouveau champ est introduit. Ce champ est appelé potentiel de frittage et contient les informations sur l’état du matériau pendant le procédé. Sa valeur est 0 en poudre libre; 1 correspond à un matériau plein entièrement dense.
La conductivité thermique effective k dépend du potentiel de frittage: k = k (Φ). Lors du procédé, la conductivité thermique effective d’un milieu évolue de la valeur kp d’une poudre libre à la valeur kb correspondant à un matériau plein et peut être reliée au potentiel de frittage Φ en interpolant entre kp et kb:
![]()

Publications liées
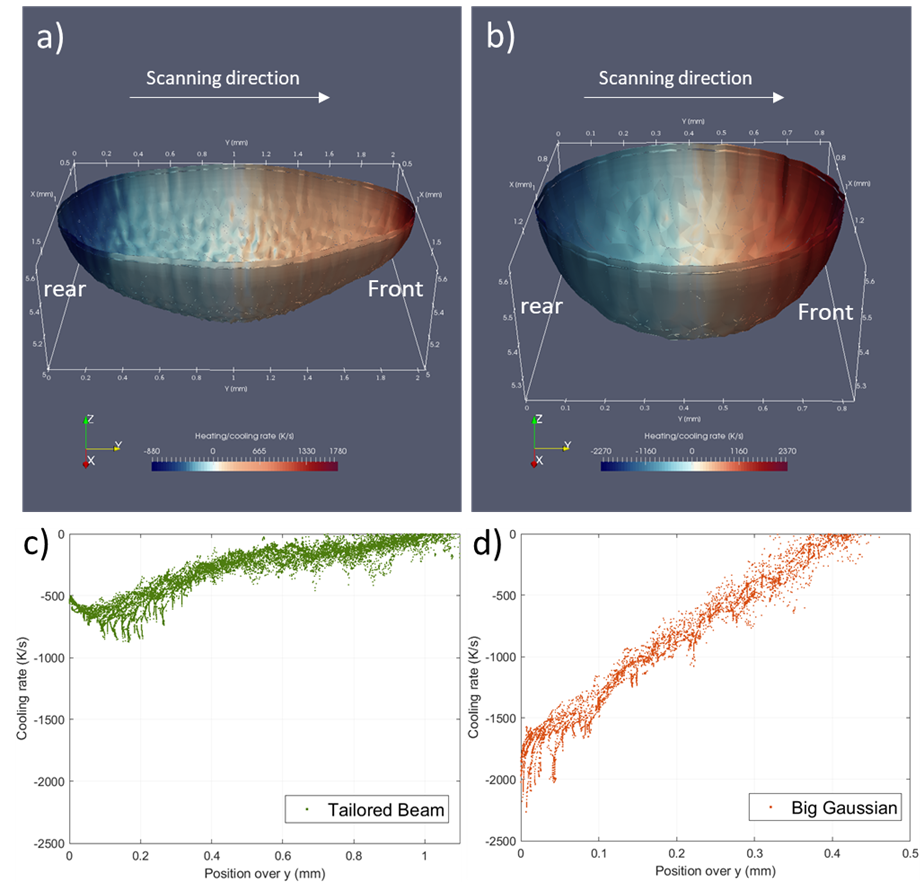
Esmaeilzadeh, J. Jhabvala, L. Schlenger, M. van der Meer, E. Boillat, C. Cayron, A.M. Jamili, J. Xiao, R.E. Logé, Toward Architected Microstructures Using Advanced Laser Beam Shaping in Laser Powder Bed Fusion of Ti-6Al-4V, Adv. Funct. Mater. 2420427 (2025) 1–17. https://doi.org/10.1002/adfm.202420427.
Schlenger, M.H. Nasab, G. Masinelli, E. Boillat, J. Jhabvala, T. Ivas, C. Navarre, R. Esmaeilzadeh, J. Yang, C. Leinenbach, P. Hoffmann, K. Wasmer, R.E. Logé, Fast and accurate laser powder bed fusion metamodels predicting melt pool dimensions, effective laser absorptivity and lack of fusion defects, J. Manuf. Process. 141 (2025) 1337–1353. https://doi.org/10.1016/j.jmapro.2025.03.006.
A.M. Jamili, J. Jhabvala, S. Van Petegem, D. Weisz-Patrault, E. Boillat, J. Nohava, A. Özsoy, S. Banait, N. Casati, R.E. Logé, Avoiding cracks in multi-material printing by combining laser powder bed fusion with metallic foils: Application to Ti6Al4V-AlSi12 structures, Addit. Manuf. 97 (2025). https://doi.org/10.1016/j.addma.2024.104615.
B. Meylan, A. Masserey, E. Boillat, I. Calderon, K. Wasmer. Thermal Modelling and Experimental Validation in the Perspective of Tool Steel Laser Polishing. Applied Science, 2022, 12, 8409. https://doi.org/10.3390/app12178409.
H. Ghasemi-Tabasi, C. de Formanoir, S. Van Petegem, J. Jhabvala, S. Hocine, E. Boillat, N. Sohrabi, F. Marone, D. Grolimund, H. Van Swygenhoven, R. E. Logé, Direct observation of crack formation mechanisms with operando Laser Powder Bed Fusion X-ray imaging, Additive Manufacturing, Volume 51, 2022, 102619, ISSN 2214-8604, https://doi.org/10.1016/j.addma.2022.102619.
N. Sohrabi, J. Jhabvala, G. Ku., M. Stoica, A. Parrilli, S. Berns, E. Polatidis, S. Van Petegem, S. Hugon, A. Neels, J. F. Löffler, R. E. Logé, Characterization, mechanical properties and dimensional accuracy of a Zr-based bulk metallic glass manufactured via laser powder-bed fusion, Materials & Design, Volume 199, 2021, 109400, ISSN 0264-1275, https://doi.org/10.1016/j.matdes.2020.109400.
H. Ghasemi-Tabasi, J. Jhabvala, E. Boillat, T. Ivas, R. Drissi-Daoudi, R. E. Logé, An effective rule for translating optimal selective laser melting processing parameters from one material to another, Additive Manufacturing, Volume 36, 2020, 101496, ISSN 2214-8604, https://doi.org/10.1016/j.addma.2020.101496.
T. Polivnikova, E. Boillat, R. Glardon, Study and Modelling of the Melt Pool Dynamics during Selective Laser Sintering and Melting, EPFL PhD thesis, 2015. https://infoscience.epfl.ch/record/213654.
S. Kolossov, E. Boillat, R. Glardon, Non-linear model and finite element simulation of the selective laser sintering process, EPFL PhD thesis, 2005. https://infoscience.epfl.ch/record/33647.
S. Kolossov, E. Boillat, R. Glardon, P. Fischer, M. Locher, 3D FE simulation for temperature evolution in the selective laser sintering process, International Journal of Machine Tools and Manufacture, Volume 44, Issues 2–3, 2004, Pages 117-123, ISSN 0890-6955. https://doi.org/10.1016/j.ijmachtools.2003.10.019.
E. Boillat, Finite element methods on non-conforming grids by penalizing the matching constraint, ESAIM M2AN. 37 (2003) 357–372. https://doi.org/10.1051/m2an:2003031.