Coating of a liquid film of constant and predictable thickness is crucial in several industrial applications. One way to achieve this is to use applicators made of a reservoir from which the liquid escapes by passing through a door of known height. These distance-controlled devices seem more sophisticated than force-controlled ones where the deposited thickness would depend rather on the weight of the object that is pulled. This latter configuration was studied recently by Seiwert1, both theoretically and experimentally. He used for that purpose a scraper, that is to say an inclined plate that is pulled at constant speed (Figure 1). Two aspects of his (preliminary) study would deserve a deeper analysis.
Firstly, his theoretical model uses the expression of the velocity field inside a corner derived by Taylor2. It does not allow to predict directly the deposited thickness ed because it depends on the maximum thickness upstream eM. Secondly, the model was assumed to be 2D but the experiment was actually performed in a 3D configuration. The scraper width was indeed smaller than the base plate one, meaning that the fluid escaped on the edges. The maximum thickness upstream should thus depend on the scraper width. In the 2D case, there is no reason that eM should be even constant in time so that we may get an indefinitly growing bump. Moreover, this bump is most likely to contain recirculation zones (Moffatt eddies3).
The aim of this project is to build an experimental set-up similar to the one of Seiwert, measuring the film thickness through the transparent base plate with a Confocal Chromatic Imaging technique4, investigating the effect of the scraper width on the bump size (including non-stationary effects) and visualizing recirculation zones with particles and a laser sheet.
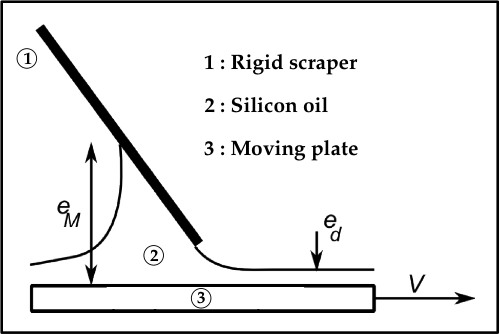
Figure 1 : Scraper configuration
1 J. Seiwert, Entraînements visqueux, PhD thesis (2010)
2 G.I. Taylor, On scraping viscous fluid from a plane surface, The Scientific Papers of Sir Geoffrey Ingram Taylor (1962)
3 H.K. Moffatt, Viscous and resistive eddies near a corner, J. of Fluid Mech. (1963)
4 http://www.stilsa.com/EN/prin.htm
Supervisor: Nicolas Kofman