To execute multiscale modeling in mechanics often requires explicit multiscale methods. Our research often uses “sequential” or “hierarchical” models, wherein information is “passed” from one scale to the next, using appropriate theories or parameters at each scale. However, some problems require “concurrent” multiscale methods wherein two or methods are intimately connected within a single computational framework. For problems involving dislocation plasticity or quantum studies of defects, such coupled models are often essential.
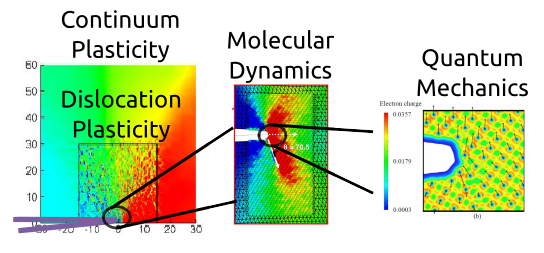
Our main contribution in the concurrent multiscale domain is the development of the Coupled Atomistic/Discrete-Dislocation (CADD) method. This method couples a fully atomistic domain to a continuum domain supporting discrete dislocation plasticity, with seamless passing of dislocations back and forth between domains as dictated by the mechanics and evolution of the problem under study. The underlying atomistic/continuum coupling is a force-based method similar to the earlier FeAt method, and these methods create no errors at the atom/continuum boundary and thus are of high accuracy for many problems. Extensions to finite temperature have been developed, mainly to handle finite-temperature atomistic domains embedded in a quasistatic finite-T continuum domain.
We are currently extending CADD to include full 3d dislocation dynamics (CADD-3d). In this effort, we are coupling two existing open-source codes, LAMMPS for MD and Paradis for DD, so that the method can be easily disseminated. CADD-3d will include dislocation loops that are simultaneously in both atomistic and continuum domains, and this coupling is challenging. Demonstration problems for the method are expected to be available soon.
We are now introducing an atomistic/continuum method based on the CADD or FeAt coupling that operates entirely within LAMMPS, where the continuum finite-element domain is included via a “fix” in LAMMPS. This approach allows the high efficiency, parallelization, system generation, library of potentials, and output tools of LAMMPS to be used within a coupled setting. In this model, the continuum remains linearly elastic but serves to remove problems with finite boundaries in standard MD calculations.
We subsequently built on the CADD concept to develop a quantum/continuum coupling method, CADD-QM, where the atomistic domain is replaced by full Kohn-Sham DFT quantum mechanics. The method is highly accurate although still requiring large DFT domains, making it computationally expensive. However, in problems with long range fields and/or non-periodic structures, such as dislocations or cracks, multiscale approaches are essential and CADD-QM provides a clean and systematically improvable method. To reduce the quantum computational domain size further, we have recently developed a new coupled method, labelled QM/MM (molecular mechanics) to follow along the nomenclature of related methods, based on the concept of constrained DFT. By applying constraints to the electron density near the quantum/continuum or quantum/atomistic interface, quantum electronic interface errors can be reduced, allowing for a reduction in the quantum cell size without loss of fidelity in the computations.
There are many methods to couple atomistics to a continuum in different spatial domains. However, such methods are still held hostage by the need for MD time scales. This largely precludes the study of problems involving time evolution, and particularly diffusion, over long distance and large times. Accelerated MD can extend the time scale of MD but only over limited length scales. Kinetic Monte Carlo methods can also extend time scales, in a more approximate manner but over larger length scales, and without full mechanical coupling as defects interact or new phases form, etc. To bridge the time-scale gap while retaining full MD resolution around defects, we are developing a new concurrent method that couples continuum diffusion and accelerated MD, with full atomistic resolution around defects, and with full coupling of diffusion including due to mechanical fields generated by the (evolving) defects. The method will be published soon, with illustrative examples such as dislocation climb.
Key publications:
- L. Shilkrot, R. Miller, and W. A. Curtin, “A Coupled Atomistic/Continuum Model for Dislocation Plasticity”, Phys. Rev. Lett. 89, #025501 (2002).
- W. A. Curtin and R. M. Miller, “Atomistic/Continuum Coupling in Computational Materials Science, Modeling and Simulation in Materials Science, 11, R33-R68 (2003).
- L. Shilkrot, R. Miller, and W. A. Curtin, “Multiscale Plasticity Modeling: Coupled Atomistics and Discrete Dislocation Mechanics”, J. Mech. Phys. Solids 52, 755-787 (2004).
- S. Qu, V. Shastry, W. A. Curtin, and R. E. Miller, “A finite-temperature dynamic coupled atomistic/discrete dislocation method”, Mod. Sim. Matls. Sci. Eng. 13, 1101-1118 (2005).
- A. Nair, D. Warner, R. Hennig, and W. A. Curtin, “Quantum/Continuum Multiscale Method applied to Dislocation nucleation at a crack tip”, Scripta Mater. 63, 1212-1215 (2010).
- X. Zhang, G. Lu, and W. A. Curtin, “Multiscale Quantum/Atomistic Coupling Using Constrained Density Functional Theory”, Phys. Rev. B (2013).
Additional work:
- M. Dewald and W. A. Curtin, “Analysis and Minimization of Dislocation Interactions with Atomistic/Continuum Interfaces“, Mod. Sim. Mat. Sci. Eng. 14, 497-514 (2006).
- M. Wallin, W. A. Curtin, M. Ristinmaa, and A. Needleman, “Multiscale plasticity modeling: coupled discrete dislocation and continuum crystal plasticity”, J. Mech. Phys. Solids 56, 3167-3180 (2008).
- K. Baker and W. A. Curtin, “Multiscale Modeling of Diffusive Processes”, in preparation. F. Pavia and W. A. Curtin, “Coupled Atomistics/Continuum: putting Finite Elements in LAMMPS”, in preparation.
- K. Baker and W. A. Curtin, Assessment of Phase-Field-Crystal Concepts using Long-time Molecular Dynamics, submitted to Phys. Rev. Lett. (2014).