Marc Kunze, Alireza Karimi, Roland Longchamp
Overview
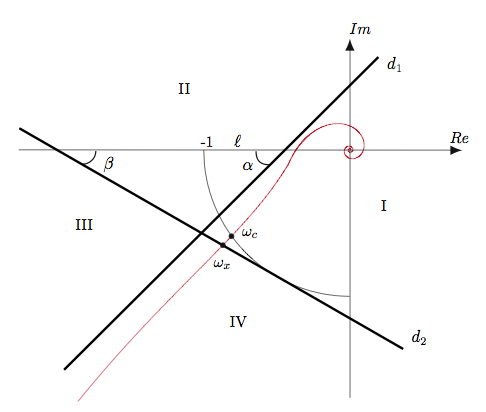
The classical robustness indicators, like the gain, phase and modulus margins, as well as the performance indicator, the crossover frequency, are nonlinear functions of the controller parameters. The optimization methods with constraints on these values lead to non-convex optimization problems and cannot be solved efficiently. The idea is to replace the classical robustness indicators by a straight line (d1) in the complex plane that ensures lower bounds on the conventional robustness margins and to approximate the crossover frequency by another straight line (d2). These two lines lead to linear constraints for the optimization problem in which robustness and/or performance are maximized. Each frequency point of the non parametric model of the system multiplied by the controller is simply constrained to be in a certain region determined by these two lines. As the number of constraints is finished, linear programming can solve this optimization problem efficiently. Thus robust controllers can be designed easily by loop shaping in the Nyquist diagram. It should be noted that the multi-model case can also be treated as it simply increases the number of constraints.
A simple extension of the method allows us to design gain-scheduled controllers. These controllers are useful when dealing with systems whose parameters change as a function of a scheduling variable. Future research is to find under which conditions these gain-scheduled controllers are globally stable.
Keywords : Linear programming; convex optimization; robustness margin; robust controller; gain-scheduled controller; non parametric model;
Related publications
[epfl_infoscience url=”https://infoscience.epfl.ch/publication-exports/2856/”]