Yvan Michellod, Philippe Müllhaupt, Denis Gillet
Overview
The consequence of the loss of involutivity of a specific set of vector fields on the periodicity of the joint motion is examined for redundant robots. An output task, defined as a one dimensional periodic closed curve embedded in a two dimensional working surface, is realized through the computation of joint velocities in the configuration space. Depending on the manner in which the joint velocity is computed from the end-effector velocity, the resulting joint motion can become unpredictable and of a chaotical nature, even though the end-effector movement is periodic and predictable. An improvement over classical pseudo-inverse computation of the joint motion is obtained by first suitably selecting two involutive vector fields (used as a basis for parameterization) in the tangent bundle of the output manifold.
An illustration of the concepts is made hereafter, considering a 5-rotative joint open-kinematic chain.
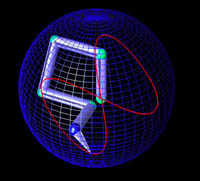
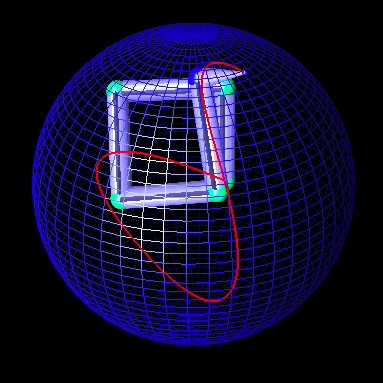
A positioning end-effector task is selected: the extremity of the robot arm realizes a Lissajou curve on a sphere in the 3-dimensional space.
Keywords : Nonlinear Control; Nano-Positionning; Overactuation; Dual-Stage;
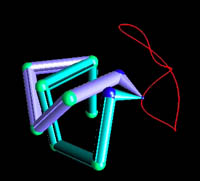
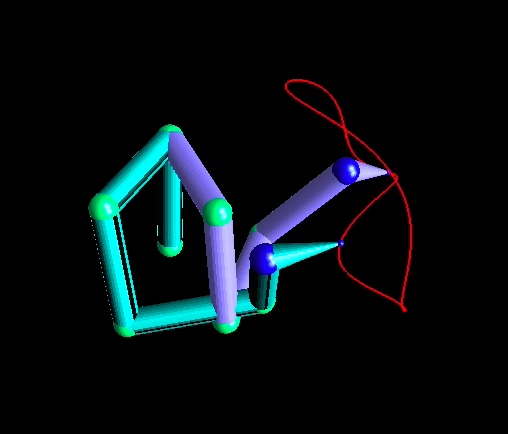
The jacobian pseudo-inversion gives us one way of obtaining the joint movement in order to realize the task. However, the resulting submersion from the 3D space into the 5D space of the robot induces chaotical and unpredictable movements of the elbow.
On Achieving Periodicity of Joints
The introduction of an involutive basis of the tangent bundle of the output manifold helps in reducing the erratic and unpredictable movement of the joints.
The following movie clearly illustrates the reduction of unpredictability of the elbow.
However, perfect periodicity is still not achieved, as the following movie illustrates: the elbow does not pass through the same configuration at successive periods of the main task.
Achieving exact periodicity through reduction of the DOF of the arm
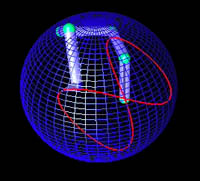
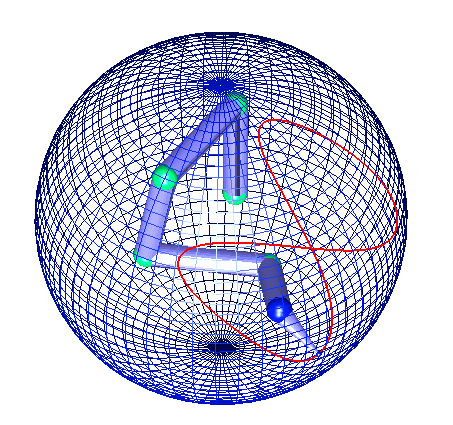
The periodicity is easily obtained when blocking 2 of the 5 degrees of freedom of the arm. However, this is achieved at the cost of a loss of flexibility. The redundancy of the arm is thus completely determined in a fixed configuration.
Achieving exact periodicity by construction of an involutive basis of the tangent bundle
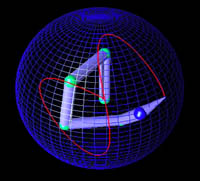
The construction of an involutive basis of the tangent bundle using complementary 1-forms induces periodic joints trajectories. This basis is obtained considering the exact 1-form of the output manifold combined with 2 arbitrary constant 1-forms. Considering the complementary space of these three 1-forms, we obtain the desired involutive basis of the tangent space bundle. Using this basis to realize the Lissajou task, we obtain perfect periodicity of the joints trajectories: the elbow of the manipulator does pass at the same configuration at successive periods of the task.
Movies
Journal Paper
Pending
Y. Michellod, P. Mullhaupt and D. Gillet, Trajectory Tracking through Overactuation for an Optical Delay Line, submitted to IEEE/ASME Transactions on Mechatronics, 2007.
[detailed record] [bibtex]
Conference paper
2008
Y. Michellod, P. Mullhaupt and D. Gillet, On Achieving Periodic Joint-Motion for Redundant Robots, , 2008.
[detailed record] [bibtex]