The non parametric model of the primary path obtained by the spectral analysis method shows that there are several vibration modes, whereas the first mode around 31,5 Hz is the most important. The second vibration mode around 160Hz should also be taken into consideration when designing the controller.
Control objective: The goal is to compute a linear discrete-time controller which minimizes the residual force around the first and second vibration modes of the primary path model and to try to distribute the amplification of the disturbances over the higher frequencies. In addition, the controller gain should be equal to zero at the frequency of Fs/2 (the term 1+z-1 should be incorporated in the controller).
More precisely, the control objective can be presented in terms of the constraints for the closed-loop sensitivity functions. The structure of the closed-loop system is given in the following figure:
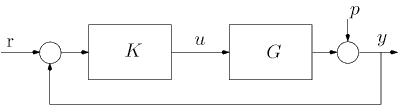
Let the output and input sensitivity functions be defined as follows:
Output sensitivity function
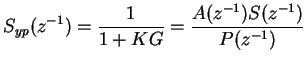
Input sensitivity function
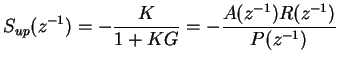
where K=R/S is the controller transfer function, G=B/A is the secondary path model, and P=AS+BR is the closed-loop characteristic polynomial.
The constraints on the output and input sensitivity functions are shown in the following two figures:
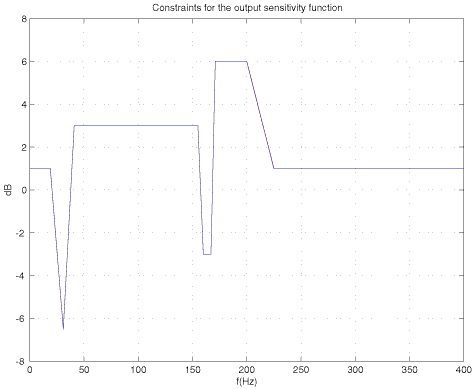
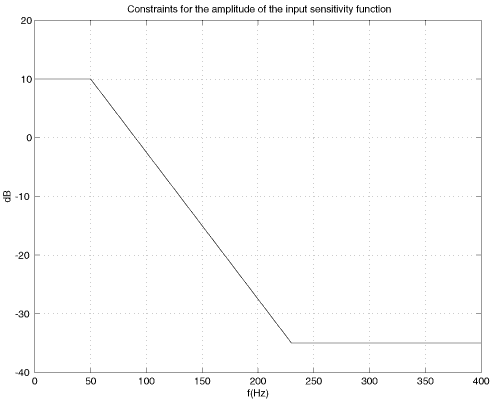
The exact values of the constraints for the output sensitivity function can be downloaded from: cons_syp.mat, and for the input sensitivity function: cons_sup.mat
Information about the real-time evaluation of the controller can be found in the controller evaluation section.
Note: The files may be downloaded by clicking on “file_name” with the right button of your mouse and choosing “save link as (Netscape)/download link to disk (Internet Explorer)” option. A compressed version of all files is available in the file: data.zip
.